2020-08-05 集训题目题解

相逢是问候

题目传送门

题目大意

给出一个长度为\(n\)的数列\(a_{1,2,...,n}\)，有\(m\)次操作，每次操作分别为以下两种：

• 对出区间\([l,r]\)，将该区间内的\(a_i\)都变为\(c^{a_i}\)，其中\(c\)为给定常数

• 给出区间\([l,r]\)，求出该区间内的\(\sum_{i=l}^{r} a_i\)

\(n,m\le 5\times 10^4\)

思路

其实我们可以发现一个事情，最后:

\[c^{c^{c^{... c^{a_i} \bmod \varphi(1)+\varphi(1)}}{\bmod \varphi(\varphi(p))+\varphi(\varphi(p))}\bmod \varphi(p)+\varphi(p)} \]

然后我们就发现到了一定程度之后再加上\(c\)都不会产生影响了。然后这个极限其实是\(\log p\)级别的（\(p\gets \varphi(p)\)），我们可以预处理一下，然后用线段树维护答案就好了，时间复杂度\(\Theta((n+m)\log n\log^2 p)\)。

然后如果我们用一下光速幂，就可以做到\(\Theta((n+m)\log n\log p)\)了。

\(\texttt{Code}\)

代码戳这里打开

Placing Squares

题目传送门

题目大意

给出一个长度为\(n\)的序列，上面有\(m\)个标记位置，我们需要在上面放正方形，并且边长为整数，正方形的边界不能是标记位置。问有多少种合法方案数。

\(n\le 10^9,m\le 10^5\)

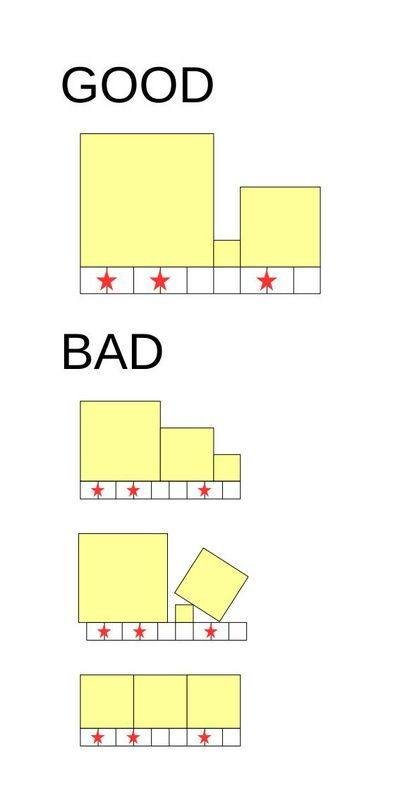
思路

首先我们可以想到一个\(\Theta(n^2)\)的dp做法，我们可以设\(f_i\)表示到点\(i\)的方案数，可以得到转移式：

\[f_u=\sum_{v=1,\texttt{v is not sign}}^{n}f_v(u-v)^2 \]

但是这个做法根本没有办法优化到\(\Theta(n)\)。我们考虑组合意义。我们可以把问题转换成：有\(n\)个位置，在\(n+1\)个位置里插板，有\(m\)个位置不能插板，并且两个板子之间方放且仅放两个不同颜色小球的方案数。那我们又可以考虑dp了。我们可以设\(dp_{i,0/1/2}\)表示当前段放了\(0/1/2\)个小球的方案数，为了方便，我们在放\(1\)个小球的时候不考虑差别，在\(2\)个小球的时候考虑。

可以得到转移式：

• 如果点\(i\)和\(i-1\)之间不能插板

\[dp_{i,0}\gets dp_{i-1,0} \]

\[dp_{i,1}\gets dp_{i-1,1}+dp_{i-1,0} \]

\[dp_{i,2}\gets dp_{i-1,0}+2dp_{i-1,1}+dp_{i-1,2} \]

• 如果点\(i\)和\(i-1\)放插板

\[dp_{i,0}\gets dp_{i-1,2} \]

\[dp_{i,1}\gets dp_{i-1,2} \]

\[dp_{i,2}\gets dp_{i-1,2} \]

然后我们就发现我们可以使用矩阵加速了，大概长成这个样子:

• 如果点\(i\)没有限制

\[\begin{bmatrix}2&2&1\\1&1&1\\1&0&1\end{bmatrix}\begin{bmatrix}dp_{i-1,2}\\dp_{i-1,1}\\dp_{i-1,0}\end{bmatrix}=\begin{bmatrix}dp_{i,2}\\dp_{i,1}\\dp_{i,0}\end{bmatrix} \]

• 如果点\(i\)有限制

\[\begin{bmatrix}1&2&1\\0&1&1\\0&0&1\end{bmatrix}\begin{bmatrix}dp_{i-1,2}\\dp_{i-1,1}\\dp_{i-1,0}\end{bmatrix}=\begin{bmatrix}dp_{i,2}\\dp_{i,1}\\dp_{i,0}\end{bmatrix} \]

于是，我们就可以在\(\Theta(m\log n)\)的时间复杂度解决这个问题。

\(\texttt{Code}\)

代码戳这里打开

组合数问题2

题目传送门

题目大意

给出\(n,k\)，求出\(0\le b\le a\le n\)的\(\dbinom{a}{b}\)前\(k\)大值的和。保证合法。答案对\(10^9+7\)取模。

\(n\le 10^6,k\le 10^5\)

思路

其实和海上钢琴师那道题挺像的。我们可以直接建一个优先队列，对于每一个\(a\)装进组合数最大的且没有计算过的答案，然后搞一下就好了。但是不能取模的话我们就得取\(\ln\)来判断两个组合数之间的大小，不过这道题并没有卡精度，所以也不是很麻烦，具体见代码。

\(\texttt{Code}\)

代码戳这里打开

Anticube

题目传送门

题目大意

给出一个长度为\(n\)的\(a_{1,2,...,n}\)问有多少种选取方法使得选出来的数两两相乘都不是立方数。

\(n\le 10^5,a_i\le 10^{10}\)

思路

首先不难想到先把立方因子删去，然后我们发现如果我们去重了的话，与一个数相乘构成立方数的数其实是唯一的，然后我们两个数之间显然只能选一个数，我们就可以贪心一下选出现次数多的那个。

一个小问题就是我们如何快速求出与一个数匹配的，不难想到的是，对于小于等于\(\sqrt[3]{a_i}\)的质因数我们可以爆枚，其余部分我们判断一下是不是完全平方数即可。具体见代码。

\(\texttt{Code}\)

代码戳这里打开

Company Acquisitions

题目传送门

题目大意

\(n\le 500\)

思路

你给我说\(3200\)的题是紫题？

这个题确实很妙，如果你想不到的话你可能一分都得不到。我们可以考虑对一个状态构造函数\(f(S)=\sum_{i=1}^{n}(2^{t_i}-1)\)，其中\(t_i\)表示附属于\(i\)的公司的个数。

我们考虑当公司之间发生吞并的时候该函数的变化。假设是分别有\(p,q\)个附属公司的两个公司之间发生的合并，可以得到:

\[\Delta=\dfrac{1}{2}((2^{p+1}-1)-(2^p-1)-(2^q-1))+\dfrac{1}{2}((2^{q+1}-1)-(2^p-1)-(2^q-1))=1 \]

然后我们就发现答案其实就是目标状态的\(f(s)\)减去初始状态的\(f(S)\)。。。

时间复杂度\(\Theta(n)\)，所以这个\(n\le 500\)其实就是拿来迷惑人的。。。

\(\texttt{Code}\)

代码戳这里打开

Yes or No

题目传送门

题目大意

\(n,m\le 10^6\)

思路

不难想到一个\(\Theta(n\times m)\)的dp做法，我们可以设\(f_{i,j}\)表示还剩\(i\)个Yes,\(j\)个No的最大期望猜对次数。可以得到转移式:

\[f_{i,j}=\dfrac{i}{i+j}f_{i-1,j}+\dfrac{j}{i+j}f_{i,j-1}+\dfrac{\max(i,j)}{i+j} \]

应该很好理解，这里就不解释了。

但是我们发现这个式子其实根本没有办法进行优化了，所以只能舍弃掉。

我们重新考虑，可以想到的是，我们一定可以猜中\(\max(n,m)\)次，如果我们把猜Yes想做往下走，猜No想做往左走，从\((n,m)\)出发，那么多余的答案就是我们经过\(y=x\)这条直线的期望次数乘上\(\dfrac{1}{2}\)（此时才Tes或No都是\(\dfrac{1}{2}\)的概率猜对），可以得到答案就是:

\[\frac{1}{2}\dfrac{\sum_{i=1}^{i\le \min(n,m)} \binom{2i}{i}\binom{n+m-2i}{n-i}}{\binom{n+m}{n}} \]

于是，我们就可以在\(\Theta(n)\)的时间复杂度内解决这个问题了。

\(\texttt{Code}\)

代码戳这里打开