关节点

关节点概念

　　删去顶点v以及v关联的各边之后，将图的一个连通分量分割成两个或两个以上的连通分量，则称顶点v为图的一个关节点（articulationpoint）

图经深度优先遍历,深度优先前序遍历给节点v编号(编号的值用visited[v]表示),
对于祖先k，子节点w，一定有visited[k]<visited[w]。

节点一共有三种，分别对它们进行关节点分析：
1、根节点，若生成树的根节点有两颗或两颗以上的子树，则根节点为关节点。

　　子树之间除了根节点,必然没有关联。
　　因为如果还有其他关联，深度优先遍历会将子树合并。根节点是子树之间唯一的关联，所以如果有多棵子树，那么根节点一定是关节点。
　　同理，任一节点的子树之间均没有关联，换句话说，
　　一个节点所关联的只可能是祖先或者自身子树中的节点。

2、分支节点，如果其子树没有指向祖先的回边，那么该节点为关节点。

　　如果除去该节点，该节点的子树将与树分割开，所以该节点为关节点。

3、子叶节点，子叶节点一定不是关节点。
　　子叶节点无论与祖先有无关联，都不会分割连通分量，所以子节点一定不是关节点。

根节点和子叶的判定都没有问题，但是分支节点如何判定子树没有指向祖先的回边呢？
我们可以通过low（v）函数来表示，low(v)表示以v为根的子树能够访问到的节点编号最小的值。
即low(v)>=visited[v],则v的子树中不存在有指向v祖先的回边。

　　low函数采用递归定义

　　 

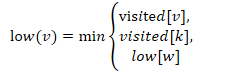
　　对于函数有几点说明：
　　1、k是与节点v有关联的祖先
　　2、w是节点v的子节点
　　3、递归函数需要有终结状态，当v是子叶时，不存在low[w],结束递归。

 

　　实现技巧：编号通过前序遍历生成，low[w]通过后续遍历生成，可通过判断在同一深度遍历完成。
　　　　判断依据，根据编号先序遍历特点，编号存在则为祖先，不存在则为孩子。

具体代码参看《数据结构C语言版》 作者 严蔚敏，吴伟民 P176-178