【算法】AC 自动机

1. 算法简介

AC 自动机，是用来多模式匹配串的算法。最好可以做到 \(O(\sum |t_i|\times |\sigma| + |s|)\)。（预处理 \(O(\sum |t_i|\times |\sigma| )\)，查询时间复杂度为 \(O(|s|)\)）。

2. 算法流程

AC 自动机可以处理这样的问题：给定 \(n\) 个匹配串和一个模式串，求出模式串中出现了多少个匹配串。

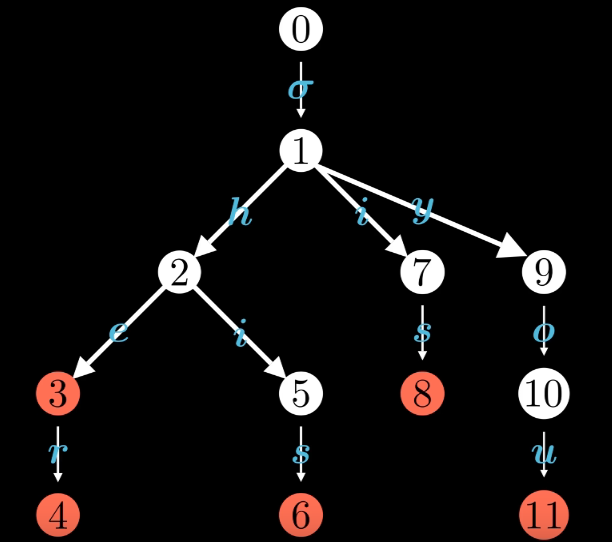
首先，对于给定的匹配串 \(t_i\) 构造出 trie 树。例如：有 \(5\) 个匹配串，you，is，her，he，his，可以构造出如下 trie 树。

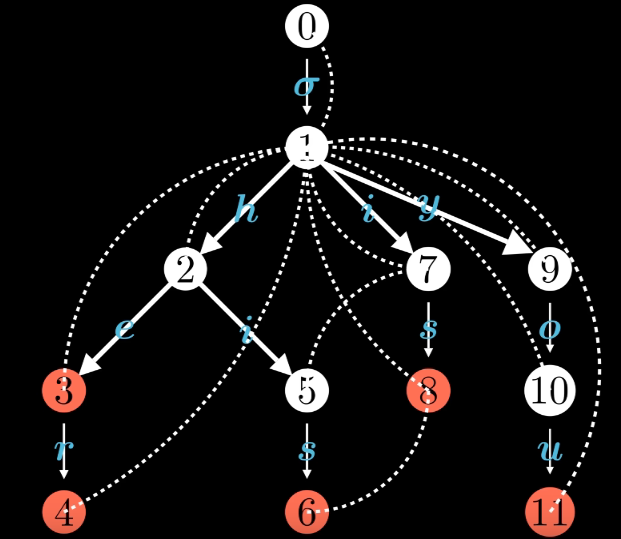
然后对于 trie 树上连失配边，即 trie 上当前位置若失配，则可以通过走 \(fail\) 边来继续完成匹配。

\(fail\) 边的连边规则为以下：

• 若当前点存在字符 \(ch\) 儿子，则让她的儿子连向当前失配边连向的那个点的字符 \(ch\) 儿子。

如下图：

这样通过遍历文本串和在 tire 树上不停地跳节点可以匹配完所有的模式串。

但是注意，统计出现的模式串的过程需要不断地跳 \(fail\) 来统计。这样暴力跳 \(fail\) 的时间复杂度为 \(O(|s|\times \sum t_i)\)。明显假掉。

我们可以利用延迟统计的思想，将贡献标记在 trie 树上，然后在树上拓扑排序，计算 \(ans_i\) 表示 \(i\) 可以被多少模式串跳到。这样的时间复杂度为 \(O(|s|)\)。

总时间复杂度为 \(O(\sum |t_i|\times |\sigma| + |s|)\)。非常优秀。

3. 算法实现

3.1 建立 trie 树

void insert(string S, int ip) {
  int p = 0;
  for (reg int i = 0; i < S.size(); ++i) {
    if(!t[p][S[i] - 'a']) {
      t[p][S[i] - 'a'] = ++idx;
    }
    p = t[p][S[i] - 'a'];
  }
  if(!id[p]) {
    id[p] = ip;
  }
  pos[ip] = id[p];
  return ;
}

3.2 计算 fail

void Fail() {
  queue<int> q;
  For(i,0,25) {
    if(t[0][i]) fail[t[0][i]] = 0, q.push(t[0][i]);
  }
  while(!q.empty()) {
    int u = q.front();
    q.pop();
    For(i,0,25) {
      if(t[u][i]) fail[t[u][i]] = t[fail[u]][i], in[t[fail[u]][i]]++, q.push(t[u][i]);
      else t[u][i] = t[fail[u]][i];
    }
  }
}

3.3 贡献标记

void query() {
  int u = 0;
  For(i,1,n) {
    u = t[u][T[i] - 'a'];
    num[u]++;
  }
  return ;
}

3.4 拓扑排序统计答案

void kahn() {
  queue<int> q;
  For(i,0,idx) {
    if(!in[i]) {
      q.push(i);
    }
  }
  while(!q.empty()) {
    int x = q.front();
    q.pop();
    ans[id[x]] = num[x];
    int y = fail[x];
    num[y] += num[x];
    if(!(--in[y])) q.push(y);
  }
  return ;
}

3.5 模版

P5357 【模板】AC 自动机

#include<bits/stdc++.h>
#define int long long
#define reg register
#define For(i,l,r) for(reg int i=l;i<=r;++i)
#define FOR(i,r,l) for(reg int i=r;i>=l;--i)

using namespace std;

bool Start;

const int N = 2e6 + 10, M = 26;

int n, m, t[N][M], id[N], pos[N], fail[N], num[N], ans[N], in[N], idx;

char T[N];

void insert(string S, int ip) {
  int p = 0;
  for (reg int i = 0; i < S.size(); ++i) {
    if(!t[p][S[i] - 'a']) {
      t[p][S[i] - 'a'] = ++idx;
    }
    p = t[p][S[i] - 'a'];
  }
  if(!id[p]) {
    id[p] = ip;
  }
  pos[ip] = id[p];
  return ;
}

void Fail() {
  queue<int> q;
  For(i,0,25) {
    if(t[0][i]) fail[t[0][i]] = 0, q.push(t[0][i]);
  }
  while(!q.empty()) {
    int u = q.front();
    q.pop();
    For(i,0,25) {
      if(t[u][i]) fail[t[u][i]] = t[fail[u]][i], in[t[fail[u]][i]]++, q.push(t[u][i]);
      else t[u][i] = t[fail[u]][i];
    }
  }
}

void query() {
  int u = 0;
  For(i,1,n) {
    u = t[u][T[i] - 'a'];
    num[u]++;
  }
  return ;
}

void kahn() {
  queue<int> q;
  For(i,0,idx) {
    if(!in[i]) {
      q.push(i);
    }
  }
  while(!q.empty()) {
    int x = q.front();
    q.pop();
    ans[id[x]] = num[x];
    int y = fail[x];
    num[y] += num[x];
    if(!(--in[y])) q.push(y);
  }
  return ;
}

bool End;

signed main() {
  ios::sync_with_stdio(0);
  cin.tie(0), cout.tie(0);
  cerr << 1.0*(&Start-&End)/(1024576.00) << '\n';
  cin >> m;
  For(i,1,m) {
    string S;
    cin >> S;
    insert(S, i);
  }
  cin >> (T + 1);
  n = strlen(T + 1);
  Fail();
  query();
  kahn();
  For(i,1,m) cout << ans[pos[i]] << '\n';
  return 0;
}