【做题笔记】图论杂题选做
最小生成树
套路是找到最小生成树建模。熟悉 prim,kruskal 等最小生成树算法。
多做此类题,考场上就能从容应对了。
P2619 [国家集训队] Tree I
题面
给你一个无向带权连通图,每条边是黑色或白色。让你求一棵最小权的恰好有 \(need\) 条白色边的生成树边权和。
题目保证有解。
题解
对原图跑一次 MST,设生成树中的白色边数为 \(x\),无非就三种情况:
- \(x > need\);
- \(x < need\);
- \(x = need\);
第三种情况是我们想要的,不过情况 \(1,2\) 也时有发生,且在生成生成树时强制约定条件也是不被允许的。这时我们只需要使用 wqs 二分 来解决这样的问题。
二分一个偏移量 \(py\),将每一个白色边的权值加上 \(py\)。这样在 kruskal 排序的时候,一部分白色的边会跑到黑色边的前面或者后面。这样使得白色边的数量在生成树中变得可控。
将偏移量值域范围设大一点能增加准确性。由于此题一定有解,加上可能会出现 \(py\) 时 \(x < need\),\(py + 1\) 时 \(x > need\) 的情况,这是我们只需要在 \(x \ge need\) 更新 \(ans = sum - mid \times need\) 就行了。
时间复杂度 \(O(m \log m)\)
代码
#include <bits/stdc++.h>
#define int long long
#define H 19260817
#define rint register int
#define For(i,l,r) for(rint i=l;i<=r;++i)
#define FOR(i,r,l) for(rint i=r;i>=l;--i)
#define MOD 1000003
#define mod 1000000007
using namespace std;
inline int read() {
rint x=0,f=1;char ch=getchar();
while(ch<'0'||ch>'9'){if (ch=='-') f=-1;ch=getchar();}
while(ch>='0'&&ch<='9'){x=(x<<1)+(x<<3)+(ch^48);ch=getchar();}
return x*f;
}
void print(int x){
if(x<0){putchar('-');x=-x;}
if(x>9){print(x/10);putchar(x%10+'0');}
else putchar(x+'0');
return;
}
const int N = 2e5 + 10;
struct Node {
int u, v, w, col;
bool operator < (const Node &x) const {
if(x.w != w) return w < x.w;
return col < x.col;
}
} e[N];
int n, m, k, sum, tmp, ans, f[N], cnt;
int find(int x) {
return (x == f[x] ? x : f[x] = find(f[x]));
}
void kruskal() {
sort(e + 1, e + m + 1);
For(i,1,m) {
int x = find(e[i].u), y = find(e[i].v);
if(x == y) continue;
cnt++;
f[x] = y;
if(!e[i].col) tmp++;
sum += e[i].w;
if(cnt == n-1) break;
}
}
signed main() {
n = read(), m = read(), k = read();
For(i,1,m) {
int u = read(), v = read(), w = read(), col = read();
e[i] = (Node) {u + 1, v + 1, w, col};
}
int l = -151, r = 151;
while(l <= r) {
int mid = (l + r) >> 1;
For(i,1,n) f[i] = i;
For(i,1,m) if(!e[i].col) e[i].w += mid;
sum = tmp = cnt = 0;
kruskal();
if(tmp >= k) {
l = mid + 1;
ans = sum - mid * k;
} else {
r = mid - 1;
}
For(i,1,m) if(!e[i].col) e[i].w -= mid;
}
cout << ans << '\n';
return 0;
}
P5994 [PA2014] Kuglarz
题面
有 \(n\) 个杯子,某些杯子底下会藏有一个小球,花费 \(c_{i,j}\) 可以得知 \(i\) 到 \(j\) 小球的总数的奇偶性。问至少需要花费多少元,才能保证猜出哪些杯子底下藏着球。
题解
最小生成树好题 !!
第 \(i\) 个杯子中是否有小球可以通过两种方式来判断:
- 花费 \(c_{i,i}\) 的代价查询 \(i\) 的奇偶性;
- 花费 \(c_{i,j},c_{i+1,j}\) 的代价查询 \(i\) 到 \(j\) 和 \(i+1\) 到 \(j\) 的奇偶性;
由于 \(i\) 与 \(i-1\) 的信息不好合并,于是可以把区间拆成“左开右闭”。这样,\((i,i]\) 的答案相当于区间 \([i-1,i]\) 的答案。
我们可以将两种方式看作是两种边,杯子看作点(多了一个“0”点杯子,这个杯子不需要管)。现在希望这张由杯子构成的图上的生成树最小。于是求最小生成树就可以了。
时间复杂度 \(O(n^2 \log n^2)\) (用 kruskal cǎo 过去了)。
代码
#include <bits/stdc++.h>
#define int long long
#define H 19260817
#define rint register int
#define For(i,l,r) for(rint i=l;i<=r;++i)
#define FOR(i,r,l) for(rint i=r;i>=l;--i)
#define MOD 1000003
#define mod 1000000007
using namespace std;
inline int read() {
rint x=0,f=1;char ch=getchar();
while(ch<'0'||ch>'9'){if (ch=='-') f=-1;ch=getchar();}
while(ch>='0'&&ch<='9'){x=(x<<1)+(x<<3)+(ch^48);ch=getchar();}
return x*f;
}
void print(int x){
if(x<0){putchar('-');x=-x;}
if(x>9){print(x/10);putchar(x%10+'0');}
else putchar(x+'0');
return;
}
const int N = 2e3 + 10, M = 4e6 + 10;
struct Node {
int u, v, w;
bool operator < (const Node &x) const {
return w < x.w;
}
} e[M];
int n, tot, f[N], ans;
int find(int x) {
return (x == f[x] ? x : f[x] = find(f[x]));
}
void kruskal() {
sort(e + 1, e + tot + 1);
For(i,1,tot) {
int x = find(e[i].u), y = find(e[i].v);
if(x == y) continue;
f[x] = y;
ans += e[i].w;
}
}
signed main() {
n = read();
For(i,1,n) {
For(j,i,n) {
e[++tot] = (Node) {i-1, j, read()};
}
}
For(i,1,n) f[i] = i;
kruskal();
cout << ans << '\n';
return 0;
}
边双联通分量
CF231E Cactus
题面
给定一张 \(n\) 个点 \(m\) 条边的简单连通图,且每个点最多属于一个简单环。有 \(q\) 次询问,每次询问给出两个整数 \(x\),\(y\)。问从 \(x\) 到 \(y\) 有多少个简单路径。
题解
边双的板子。
先对于整张图缩边双,然后使整个图变成一个由边双组成的树。
对于一次询问,相当于树上路径基于环计数。
我们发现在 \(u \to lca(u,v) \to v\) 这个路径上的边双数与答案息息相关。对于一个环要么走左边,要么走右边走到其父节点。故每一个环会使答案贡献翻倍。即令 \(x\) 为 \(u \to v\) 路径上的边双数,则答案为 \(2^x\)。
缩边双直接 Tarjan 求就行了。
求桥时,链式前向星的边数要从 \(2\) 开始统计,别问我为啥知道,血与泪的教训!
时间复杂度 \(O(q \log n)\)。
代码
#include <bits/stdc++.h>
#define int long long
#define rint register int
#define For(i,l,r) for(rint i=l;i<=r;++i)
#define FOR(i,r,l) for(rint i=r;i>=l;--i)
#define MOD 1000003
#define mod 1000000007
using namespace std;
inline int read() {
rint x=0,f=1;char ch=getchar();
while(ch<'0'||ch>'9'){if (ch=='-') f=-1;ch=getchar();}
while(ch>='0'&&ch<='9'){x=(x<<1)+(x<<3)+(ch^48);ch=getchar();}
return x*f;
}
void print(int x){
if(x<0){putchar('-');x=-x;}
if(x>9){print(x/10);putchar(x%10+'0');}
else putchar(x+'0');
return;
}
const int N = 2e5 + 10;
struct Node {
int v, nx;
} e[N], E[N];
int n, m, tot = 1, TOT = 1, idx, h[N], H[N], cnt, anc[N][50], dep[N], siz[N], dis[N], dfn[N], low[N], dcc[N], t;
bool f[N];
void add(int u, int v) {
e[++tot].v = v, e[tot].nx = h[u], h[u] = tot;
}
void Add(int u, int v) {
E[++TOT].v = v, E[TOT].nx = H[u], H[u] = TOT;
}
void tarjan(int x, int la) {
dfn[x] = low[x] = ++idx;
for (int i = h[x]; i; i = e[i].nx) {
int y = e[i].v;
if(!dfn[y]) {
tarjan(y, i);
if(dfn[x] < low[y]) f[i] = f[i ^ 1] = 1;
low[x] = min(low[x], low[y]);
} else if(i != (la ^ 1)) {
low[x] = min(low[x], dfn[y]);
}
}
}
void dfs(int x, int col) {
dcc[x] = col;
siz[col]++;
for (int i = h[x]; i; i = e[i].nx) {
int y = e[i].v;
if(dcc[y] || f[i]) continue;
dfs(y, col);
}
}
void dfs1(int x, int fa) {
dis[x] += (siz[x] > 1);
for (int i = H[x]; i; i = E[i].nx) {
int y = E[i].v;
if(y == fa) continue;
anc[y][0] = x;
dis[y] = dis[x];
dep[y] = dep[x] + 1;
dfs1(y, x);
}
}
void init() {
For(j,1,t) {
For(i,1,n) {
anc[i][j] = anc[anc[i][j-1]][j-1];
}
}
}
int lca(int x, int y) {
if(dep[x] < dep[y]) swap(x, y);
FOR(i,t,0) {
if(dep[anc[x][i]] >= dep[y]) x = anc[x][i];
}
if(x == y) return x;
FOR(i,t,0) {
if(anc[x][i] != anc[y][i]) x = anc[x][i], y = anc[y][i];
}
return anc[x][0];
}
int qpow(int a, int b) {
int res = 1;
a %= mod;
while(b) {
if(b & 1) res = res * a % mod;
a = a * a % mod, b >>= 1;
}
return res;
}
signed main() {
n = read(), m = read();
For(i,1,m) {
int u = read(), v = read();
add(u, v);
add(v, u);
}
tarjan(1, -1);
For(i,1,n) {
if(!dcc[i]) dfs(i, ++cnt);
}
For(i,1,n) {
for (int j = h[i]; j; j = e[j].nx) {
int y = e[j].v;
if(dcc[i] != dcc[y]) Add(dcc[i], dcc[y]);
}
}
t = __lg(n) + 1;
dep[1] = 1;
dfs1(1, 0);
init();
int T = read();
while(T--) {
int x = read(), y = read();
int LCA = lca(dcc[x], dcc[y]);
x = dcc[x], y = dcc[y];
cout << qpow(2, dis[x] + dis[y] - dis[LCA] - dis[anc[LCA][0]]) % mod << '\n';
}
return 0;
}
CF652E Pursuit For Artifacts
题面
给定一张 \(n\) 个点 \(m\) 条边的简单无向连通图。边权为 \(w \in \{0,1\}\)。在每条边只能经过一次的情况下,求是否存在一条从 \(a\) 到 \(b\) 的路径,满足路径上至少存在一条权为 \(1\) 的边。
题解
和上一道题一样,缩边双,重建边双树,dfs,统计答案。
学到了一个新的缩边双的方法:
void tarjan(int x, int fa) {
dfn[x] = low[x] = ++idx;
stk[++top] = x, ins[x] = 1;
for (int i = h[x]; i; i = e[i].nx) {
int y = e[i].v;
if(y == fa) continue;
if(!dfn[y]) {
tarjan(y, x);
low[x] = min(low[x], low[y]);
} else if(ins[y]) low[x] = min(low[x], dfn[y]);
}
if(dfn[x] == low[x]) {
int y;
dcc[x] = ++col;
do {
y = stk[top--];
dcc[y] = col;
ins[y] = 0;
} while(y != x);
}
}
但是在有重边的情况下会寄掉。
只比强连通分量 Tarjan 多记了一个父亲(因为是无向图)。对于我这种“求同存异”的选手来说,实在是太香了/kk。
代码
#include <bits/stdc++.h>
#define ll long long
#define H 19260817
#define rint register int
#define For(i,l,r) for(rint i=l;i<=r;++i)
#define FOR(i,r,l) for(rint i=r;i>=l;--i)
#define MOD 1000003
#define mod 1000000007
using namespace std;
inline int read() {
rint x=0,f=1;char ch=getchar();
while(ch<'0'||ch>'9'){if (ch=='-') f=-1;ch=getchar();}
while(ch>='0'&&ch<='9'){x=(x<<1)+(x<<3)+(ch^48);ch=getchar();}
return x*f;
}
void print(int x){
if(x<0){putchar('-');x=-x;}
if(x>9){print(x/10);putchar(x%10+'0');}
else putchar(x+'0');
return;
}
const int N = 3e5 + 10;
struct Node {
int u, v, nx;
bool w;
} e[N << 1];
int n, m, h[N], tot, dcc[N], low[N], dfn[N], col, idx, stk[N], top, ins[N], s, t, vis[N];
bool f[N];
void add(int u, int v, bool w) {
e[++tot].u = u, e[tot].v = v, e[tot].w = w, e[tot].nx = h[u], h[u] = tot;
}
void tarjan(int x, int fa) {
dfn[x] = low[x] = ++idx;
stk[++top] = x, ins[x] = 1;
for (int i = h[x]; i; i = e[i].nx) {
int y = e[i].v;
if(y == fa) continue;
if(!dfn[y]) {
tarjan(y, x);
low[x] = min(low[x], low[y]);
} else if(ins[y]) low[x] = min(low[x], dfn[y]);
}
if(dfn[x] == low[x]) {
int y;
dcc[x] = ++col;
do {
y = stk[top--];
dcc[y] = col;
ins[y] = 0;
} while(y != x);
}
}
void dfs(int x, bool ff) {
if(f[x]) ff = 1;
if(x == t) {
if(ff) puts("YES");
else puts("NO");
exit(0);
}
vis[x] = 1;
for (int i = h[x]; i; i = e[i].nx) {
int y = e[i].v;
if(!vis[y]) dfs(y, ff | e[i].w);
}
}
signed main() {
n = read(), m = read();
For(i,1,m) {
int u = read(), v = read(), w = read();
add(u, v, w);
add(v, u, w);
}
tarjan(1, 0);
for (int i = 1; i <= tot; i += 2) {
if(dcc[e[i].u] == dcc[e[i].v] && e[i].w) f[dcc[e[i].u]] = 1;
}
memset(h, 0, sizeof h);
tot = 0;
For(i,1,m*2) {
if(dcc[e[i].u] != dcc[e[i].v]) {
add(dcc[e[i].u], dcc[e[i].v], e[i].w);
}
}
s = dcc[read()]; t = dcc[read()];
dfs(s, 0);
return 0;
}
基环树
P1453 城市环路
题面
给定一个 \(n\) 个点的带点权基环树,若两个点之间有一条边连接,如果选择了其中一端的节点,那另一段的节点则不可选择。问选择方案中点权和最大值。
题解
基环树模模模板题
很小清新的思路。把环上的一条边 bank 掉,分别令这条被 bank 掉的边所连接的点为树的根 \(s\), \(t\)。做树形 dp。
设 \(dp[i][0/1]\) 表示在以 \(i\) 为根的子树内 \(i\) 点选或不选的最大贡献。
显然有转移:
答案为 \(\max(dp[s][0],dp[t][0])\)(如果是 \(dp[s][1]\),\(dp[t][1]\) 则不能确定 \(s\) 和 \(t\) 是否会被同时选择。因为原图上 \(s\) 与 \(t\) 为父子关系)。
代码
#include <bits/stdc++.h>
#define int long long
#define H 19260817
#define rint register int
#define For(i,l,r) for(rint i=l;i<=r;++i)
#define FOR(i,r,l) for(rint i=r;i>=l;--i)
#define MOD 1000003
#define mod 1000000007
using namespace std;
inline int read() {
rint x=0,f=1;char ch=getchar();
while(ch<'0'||ch>'9'){if (ch=='-') f=-1;ch=getchar();}
while(ch>='0'&&ch<='9'){x=(x<<1)+(x<<3)+(ch^48);ch=getchar();}
return x*f;
}
void print(int x){
if(x<0){putchar('-');x=-x;}
if(x>9){print(x/10);putchar(x%10+'0');}
else putchar(x+'0');
return;
}
const int N = 4e5 + 10;
int n, m, f[N], w[N], s, t;
double dp[N][2], ans, k;
vector <int> e[N];
int find(int x) {
return (x == f[x] ? x : f[x] = find(f[x]));
}
void dfs(int x, int fa) {
dp[x][1] = w[x], dp[x][0] = 0;
for (int i = 0; i < e[x].size(); i++) {
int y = e[x][i];
if(y == fa) continue;
dfs(y, x);
dp[x][0] += max(dp[y][0], dp[y][1]);
dp[x][1] += dp[y][0];
}
return ;
}
signed main() {
n = read();
For(i,1,n) w[i] = read(), f[i] = i;
For(i,1,n) {
int u = read(), v = read();
u++, v++;
int x = find(u), y = find(v);
if(x == y) {s = u, t = v; continue;}
e[u].push_back(v);
e[v].push_back(u);
f[y] = x;
}
cin >> k;
dfs(s, 0); ans = dp[s][0];
dfs(t, 0); ans = max(ans, dp[t][0]);
printf("%.1lf\n", ans * k);
return 0;
}
P2607 [ZJOI2008] 骑士
题面
有 \(N\) 个骑士组队,每个骑士有战力,每个骑士恨一人,对于每一个人,他憎恨的人不能在与其相同的队里,选择一种安排方式使得战斗力总和最大。
题解
跟上一道题一样,也是断环做树形 \(dp\)。
注意有多个联通块,所以要分开多次进行 \(dp\)。
代码
#include <bits/stdc++.h>
#define int long long
#define H 19260817
#define rint register int
#define For(i,l,r) for(rint i=l;i<=r;++i)
#define FOR(i,r,l) for(rint i=r;i>=l;--i)
#define MOD 1000003
#define mod 1000000007
using namespace std;
inline int read() {
rint x=0,f=1;char ch=getchar();
while(ch<'0'||ch>'9'){if (ch=='-') f=-1;ch=getchar();}
while(ch>='0'&&ch<='9'){x=(x<<1)+(x<<3)+(ch^48);ch=getchar();}
return x*f;
}
void print(int x){
if(x<0){putchar('-');x=-x;}
if(x>9){print(x/10);putchar(x%10+'0');}
else putchar(x+'0');
return;
}
const int N = 2e6 + 10;
int n, m, f[N], w[N], s[N], t[N], dp[N][2], ans, tot, sum;
vector <int> e[N];
int find(int x) {
return (x == f[x] ? x : f[x] = find(f[x]));
}
void dfs(int x, int fa) {
dp[x][1] = w[x], dp[x][0] = 0;
for (int i = 0; i < e[x].size(); i++) {
int y = e[x][i];
if(y == fa) continue;
dfs(y, x);
dp[x][0] += max(dp[y][0], dp[y][1]);
dp[x][1] += dp[y][0];
}
return ;
}
signed main() {
n = read();
For(i,1,n) f[i] = i;
For(i,1,n) {
w[i] = read();
int v = read();
int x = find(i), y = find(v);
f[y] = x;
if(x == y) {s[++tot] = i, t[tot] = v; continue;}
e[i].push_back(v);
e[v].push_back(i);
}
For(i,1,tot) {
int S = s[i], T = t[i], sum = INT_MIN;
dp[S][0] = dp[T][0] = 0;
dfs(S, 0); sum = dp[S][0];
dfs(T, 0); sum = max(sum, dp[T][0]);
ans += sum;
}
printf("%lld\n", ans);
return 0;
}
最短路
P1186 玛丽卡
题面
给定一张 \(n\) 个点 \(m\) 条边的带权无向图。现在需要删除一条边,使得 \(1\) 到 \(n\) 的最短路的长度最大,输出这个最大长度。
题解
毒瘤之极!!!
令 \(dis_{i,j}\) 表示 \(i\) 到 \(j\) 的最短路径。
可以先考虑修改一条边对答案贡献的影响:
- 若改变的边不是原最短路上的边,则其对答案的贡献不会改变。
- 若改变的边是原最短路上的边,则其对答案的贡献会有影响。
于是我们可以将最短路从原图中抽离出来,
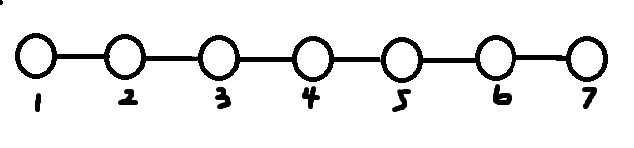
假设 \(n=7\),存在一条最短路 \(1 \to 2 \to 3 \to 4 \to 5 \to 6 \to 7\)(如上图)。
考虑现在在最短路中删去一条边,就要重新计算最短路了。
换一种思路,遍历所有除最短路以外的所有边,然后求一遍强制经过该边的最短路。
如图所示:
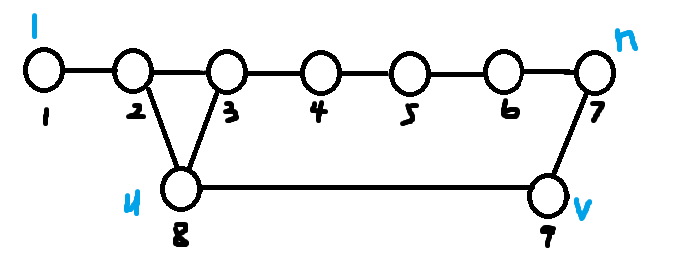
强制经过 \(u \to v\) 这条边时,最短路显然为 \(dis_{1,u} + w[u][v] + dis_{v,n}\)。
我们可以发现,这个信息可供更新 \(l1\),\(r1\) 的最短路信息。
(注意是 \(l1\),\(r1\),而不是 \(l2\),\(r1\)。因为我们想要更长的区间被更新)。
这个更新操作可以用线段树操作(区间永久\(\min\))。最后暴力枚举每一个边,统计答案。
时间复杂度 \(O(n^2 \log m)\)。
代码
#include <bits/stdc++.h>
#define ll long long
#define H 19260817
#define rint register int
#define For(i,l,r) for(rint i=l;i<=r;++i)
#define FOR(i,r,l) for(rint i=r;i>=l;--i)
#define MOD 1000003
#define mod 1000000007
#define inf 0x3f3f3f3f
#define ls p<<1
#define rs p<<1|1
using namespace std;
inline int read() {
rint x=0,f=1;char ch=getchar();
while(ch<'0'||ch>'9'){if (ch=='-') f=-1;ch=getchar();}
while(ch>='0'&&ch<='9'){x=(x<<1)+(x<<3)+(ch^48);ch=getchar();}
return x*f;
}
void print(int x){
if(x<0){putchar('-');x=-x;}
if(x>9){print(x/10);putchar(x%10+'0');}
else putchar(x+'0');
return;
}
const int M = 1e6 + 10, N = 1e3 + 10;
struct Segtree {
int l, r, tag;
} t[N << 2];
int n, m, f[N], a[N][N], d1[N], dn[N], mx, pre[N], pos[N];
bool st[N];
int find(int x) {
return (x == f[x] ? x : f[x] = find(f[x]));
}
void dij(int x, int dist[]) {
For(i,1,n) dist[i] = inf, st[i] = 0;
dist[x] = 0, pre[x] = 0;
For(i,1,n) {
int k = -1;
For(j,1,n){
if(st[j]) continue;
if(k == -1 || dist[k] > dist[j]) k = j;
}
st[k] = 1;
For(j,1,n){
if(st[j]) continue;
if(dist[j] > dist[k] + a[k][j]){
dist[j] = dist[k] + a[k][j];
pre[j] = k;
}
}
}
}
void build(int p, int l, int r) {
t[p] = (Segtree) {l, r, inf};
if(l == r) return ;
int mid = (l + r) >> 1;
build(ls, l, mid);
build(rs, mid + 1, r);
}
void up(int p, int l, int r, int w) {
if(l <= t[p].l && t[p].r <= r) {
t[p].tag = min(t[p].tag, w);
return ;
}
int mid = (t[p].l + t[p].r) >> 1;
if(l <= mid) up(ls, l, r, w);
if(r > mid) up(rs, l, r, w);
}
int query(int p, int x) {
if(t[p].l == t[p].r) {
return t[p].tag;
}
int mid = (t[p].l + t[p].r) >> 1;
if(x <= mid) return min(query(ls, x), t[p].tag);
else return min(query(rs, x), t[p].tag);
}
signed main() {
n = read(), m = read();
memset(a, 0x3f, sizeof a);
For(i,1,m) {
int u = read(), v = read(), w = read();
a[u][v] = a[v][u] = w;
}
dij(n, dn);
dij(1, d1);
For(i,1,n) f[i] = pre[i];
mx = 0;
for (int i = n; i; i = pre[i]) {
pos[i] = ++mx;
f[i] = i;
if(pre[i]) a[i][pre[i]] = a[pre[i]][i] = inf;
}
build(1, 1, mx);
For(i,1,n) {
For(j,1,n) {
if(i == j) continue;
if(a[i][j] != inf) {
int w = min(d1[i] + a[i][j] + dn[j], d1[j] + a[i][j] + dn[i]);
int x = pos[find(i)], y = pos[find(j)];
if(x > y) swap(x, y);
if(x == y) continue;
up(1, x + 1, y, w);
}
}
}
int ans = d1[n];
For(i,2,n) {
ans = max(ans, query(1, i));
}
cout << ans << '\n';
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号