test20230304考试总结(2023春 · 字符串)
前言#
赛时得分明细:
| A | B | C | D | Total | Rank |
|---|---|---|---|---|---|
| 100 | 100 | 0 | 70 | 270 | 2 |
C题如此说道:字符串没有学好的报应!!
A. P4391 [BOI2009]Radio Transmission 无线传输#
题面#
给定一个字符串
题解#
答案为
证明:
如图,假设这两段是整个字符串ss的最大公共前后缀,我将前缀和后缀分开,令它们上下一一对应;
所以推出:
-
因为上下对应相等,故第1段等于红色段;
-
因为是公共前后缀,故第2段等于第1段;
-
因为上下对应相等,故第3段等于第2段;
-
因为是公共前后缀,故第4段等于第3段;
-
......
-
红色段就是循环子串;
红色段的长度即为
代码#
#include <bits/stdc++.h>
#define int long long
#define H 19260817
#define rint register int
#define For(i,l,r) for(rint i=l;i<=r;++i)
#define FOR(i,r,l) for(rint i=r;i>=l;--i)
using namespace std;
inline int read() {
rint x=0,f=1;char ch=getchar();
while(ch<'0'||ch>'9'){if (ch=='-') f=-1;ch=getchar();}
while(ch>='0'&&ch<='9'){x=(x<<1)+(x<<3)+(ch^48);ch=getchar();}
return x*f;
}
void print(int x){
if(x<0){putchar('-');x=-x;}
if(x>9){print(x/10);putchar(x%10+'0');}
else putchar(x+'0');
return;
}
const int N = 1e6 + 10;
int n, fail[N];
char s[N];
signed main() {
n = read();
cin >> s + 1;
for (int i = 2, j = 0; i <= n; i++) {
while(j && s[i] != s[j + 1]) j = fail[j];
if(s[i] == s[j + 1]) j++;
fail[i] = j;
}
cout << n - fail[n] << '\n';
return 0;
}
B. P4824 [USACO15FEB] Censoring S#
题面#
题解#
代码#
C. P4503 [CTSC2014] 企鹅 QQ#
题面#
定义若两个账户名称是相似的,当且仅当这两个字符串等长且恰好只有一位不同。例如“Penguin1”和“Penguin2”是相似的,但“Penguin1”和“2Penguin”不是相似的。求在给定的
题解#
组合数学 + Hash
预处理出每一个字符串的前后缀
代码#
#include <bits/stdc++.h>
#define ll long long
#define ull unsigned long long
#define H 27
#define rint register int
#define For(i,l,r) for(rint i=l;i<=r;++i)
#define FOR(i,r,l) for(rint i=r;i>=l;--i)
#define MOD 1000003
#define mod 1000000007
using namespace std;
inline int read() {
rint x=0,f=1;char ch=getchar();
while(ch<'0'||ch>'9'){if (ch=='-') f=-1;ch=getchar();}
while(ch>='0'&&ch<='9'){x=(x<<1)+(x<<3)+(ch^48);ch=getchar();}
return x*f;
}
void print(int x){
if(x<0){putchar('-');x=-x;}
if(x>9){print(x/10);putchar(x%10+'0');}
else putchar(x+'0');
return;
}
const int N = 3e4 + 10, M = 205;
int n, L, S;
ull pre[N][M], nxt[N][M], p[N], ans;
char s[N][M];
pair<ull, ull> k[N];
signed main() {
n = read(), L = read(), S = read();
p[0] = 1;
For(i,1,L) p[i] = p[i - 1] * H;
For(i,1,n) {
For(j,1,L) cin >> s[i][j];
For(j,1,L) pre[i][j] = pre[i][j - 1] * H + s[i][j];
FOR(j,L,1) nxt[i][j] = nxt[i][j + 1] * H + s[i][j];
}
For(i,1,L) {
For(j,1,n) {
k[j].first = pre[j][i-1];
k[j].second = nxt[j][i+1];
}
sort(k + 1, k + n + 1);
int l = 1, r = 1;
while(r <= n) {
while(k[l] == k[r] && r <= n) r++;
r--;
ans += (((r - l + 1) * (r - l)) >> 1);
l = r + 1, r++;
}
}
cout << ans << '\n';
return 0;
}
D. P7469 [NOI Online 2021 提高组] 积木小赛#
题面#
给定两个长度为
题解#
枚举
时间复杂度
代码#
#include <bits/stdc++.h>
#define int long long
#define H 37
#define rint register int
#define For(i,l,r) for(rint i=l;i<=r;++i)
#define FOR(i,r,l) for(rint i=r;i>=l;--i)
using namespace std;
inline int read() {
rint x=0,f=1;char ch=getchar();
while(ch<'0'||ch>'9'){if (ch=='-') f=-1;ch=getchar();}
while(ch>='0'&&ch<='9'){x=(x<<1)+(x<<3)+(ch^48);ch=getchar();}
return x*f;
}
void print(int x){
if(x<0){putchar('-');x=-x;}
if(x>9){print(x/10);putchar(x%10+'0');}
else putchar(x+'0');
return;
}
const int N = 3e3 + 10;
const int M = 9e6 + 10;
int n, hs, nxt[N][156], res[M], tot;
char s[N], t[N];
signed main() {
n = read();
For(i,1,n) cin >> s[i];
For(i,1,n) cin >> t[i];
For(i,1,n) {
For(j,i,n) {
if(!nxt[i][s[j]]) nxt[i][s[j]] = j;
}
}
For(i,1,n) {
hs = 0;
int k = 1;
For(j,i,n) {
k = nxt[k][t[j]];
if(!k) break;
hs = 1ll * (hs * H) + (t[j] - 'a' + 1);
res[++tot] = hs;
k++;
}
}
sort(res + 1, res + 1 + tot);
cout << ((unique(res + 1, res + 1 + tot)) - res - 1) << '\n';
return 0;
}
作者:Daniel-yao
出处:https://www.cnblogs.com/Daniel-yao/p/17178282.html
版权:本作品采用「署名-非商业性使用-相同方式共享 4.0 国际」许可协议进行许可。

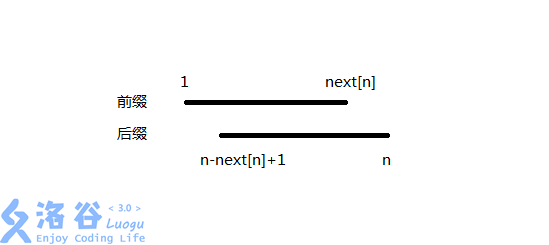




【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 地球OL攻略 —— 某应届生求职总结
· 周边上新:园子的第一款马克杯温暖上架
· Open-Sora 2.0 重磅开源!
· 提示词工程——AI应用必不可少的技术
· .NET周刊【3月第1期 2025-03-02】