【算法】单调栈 & 单调队列
1. 单调栈简介#
1.1 前言#
今天是 2023/1/15,一中寒假集训阶段性的结束了。集训的学习笔记可以在本人 blogs 的【算法】标签栏中找。
马上就要过年了,提前祝大家新年快乐!
1.2 什么是单调栈#
单调栈(monotone-stack)是一种基于栈进行的算法,且栈内元素(栈底到栈顶)都是(严格)单调递增或者单调递减的。
定义很抽象,不如拿一道题来直观的理解单调栈。
1.3 算法流程#
1.3.1 [luoguP5788]【模板】单调栈#
给出项数为
定义函数
试求出
对于
1.3.2 Solve#
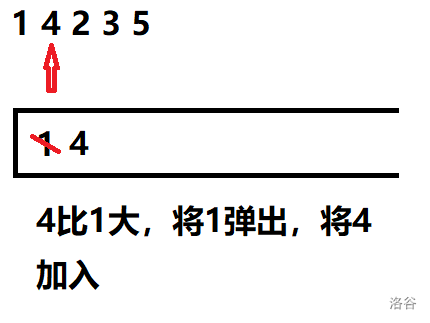
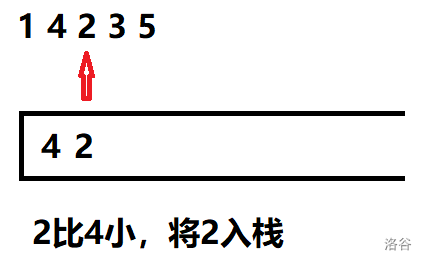
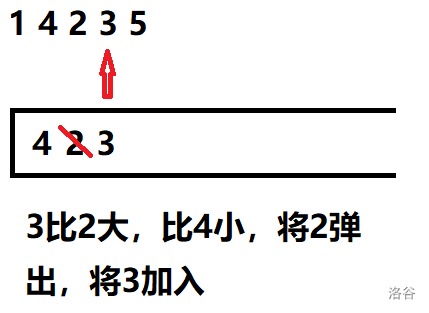
建一个单调不减栈。
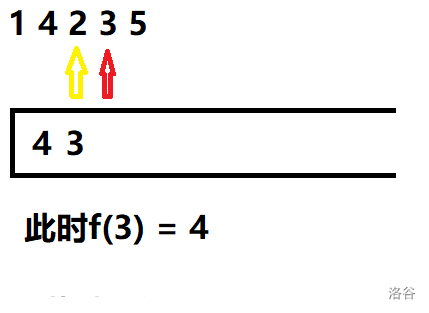
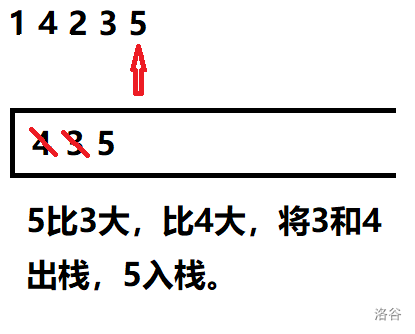
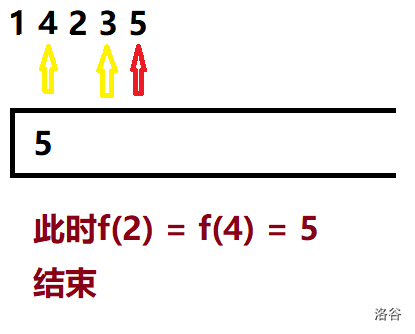
先来看一下单调栈的算法流程:
看完流程,是不是对单调栈的原理有了一定的认知了呢。
每一次加入新元素,都会从栈中弹出一些元素使得栈保持单调。通过观察发现,设栈中的一个元素在原序列中的编号为
所以每一次就在弹栈时更新答案即可。
怎么样?是不是豁然开朗。
1.4 Code & 单调栈的实现#
以上一道题为例:
#include <bits/stdc++.h>
#define ll long long
#define H 19260817
#define rint register int
#define For(i,l,r) for(rint i=l;i<=r;++i)
#define FOR(i,r,l) for(rint i=r;i>=l;--i)
#define MOD 1000003
#define mod 1000000007
using namespace std;
inline int read() {
rint x=0,f=1;char ch=getchar();
while(ch<'0'||ch>'9'){if (ch=='-') f=-1;ch=getchar();}
while(ch>='0'&&ch<='9'){x=(x<<1)+(x<<3)+(ch^48);ch=getchar();}
return x*f;
}
void print(int x){
if(x<0){putchar('-');x=-x;}
if(x>9){print(x/10);putchar(x%10+'0');}
else putchar(x+'0');
return;
}
const int N = 3e6 + 10;
int n, a[N], f[N], stk[N], tot;
signed main(){
n = read();
For(i,1,n) {
a[i] = read();
while(tot && a[stk[tot]] < a[i]){//栈顶元素比新元素小,弹栈
f[stk[tot]] = i;
--tot;
}
stk[++tot] = i;//将新元素加入单调栈中
}
For(i,1,n) {
cout << f[i] << ' ';
}
return 0;
}
1.5 单调栈时间复杂度分析#
有人会问了:上面的程序不是用了两个循环吗?两个循环不就是
并非如此,我们发现,对于一个栈来说,在最坏的情况下,一个元素会进一次栈,出一次栈。
因此我们可以看到,单调栈的时间复杂度是很优秀的。
2. 单调栈进阶#
2.1 悬线法#
我们来看一道经典的例题:
2.1.1 [luoguP1387] 最大正方形#
在一个
2.1.2 Solve#
题意就是要找到一个最大全
一眼暴力,枚举对顶点,
这一题还有别的做法吗?,肯定有,它就是——悬线法+单调栈!
把样例搬过来:
由于它是一个矩阵,所以朴素版的单调栈已经对此“无能为力”。
既然单调栈不能变成二维,那么,我们就把矩阵转化成一维。即可用悬线法转化。
我们可以枚举每一行,然后用一个
然后用单调栈维护
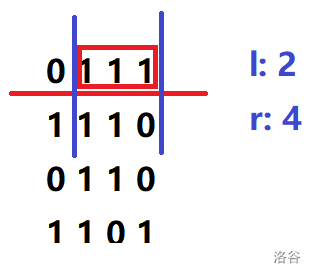
算法流程如下:
No.1
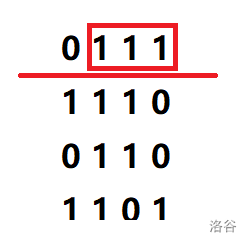
统计第一层向上连续的
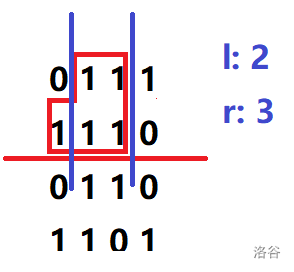
No.2
用单调栈维护
此时答案更新为
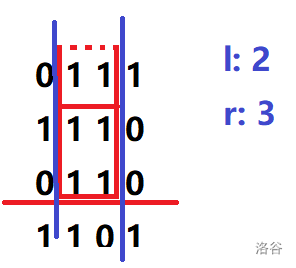
No.3
第二行亦是如此,答案更新为
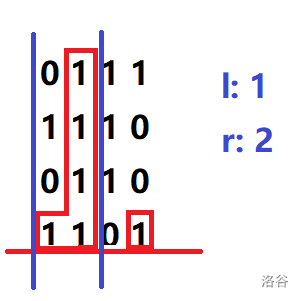
No.4
第三行,答案不做更新。
注:虚线部分表示实际答案统计的范围,已在上文中解释,不在此过多赘述。
No.5
第四行,答案不做更新。
结束,答案为
2.1.3 Code#
#include <bits/stdc++.h>
#define ll long long
#define H 19260817
#define rint register int
#define For(i,l,r) for(rint i=l;i<=r;++i)
#define FOR(i,r,l) for(rint i=r;i>=l;--i)
#define MOD 1000003
#define mod 1000000007
using namespace std;
inline int read() {
rint x=0,f=1;char ch=getchar();
while(ch<'0'||ch>'9'){if (ch=='-') f=-1;ch=getchar();}
while(ch>='0'&&ch<='9'){x=(x<<1)+(x<<3)+(ch^48);ch=getchar();}
return x*f;
}
void print(int x){
if(x<0){putchar('-');x=-x;}
if(x>9){print(x/10);putchar(x%10+'0');}
else putchar(x+'0');
return;
}
const int N = 1e2 + 10;
int n, m, h[N], a[N][N], l[N], r[N], ans, top, stk[N];
void work1() {
top = 0;
FOR(i,m,1) {
while(top && h[stk[top]] > h[i]) {
l[stk[top]] = i + 1;
top--;
}
stk[++top] = i;
}
while(top) {
l[stk[top]] = 1;
top--;
}
}
void work2() {
top = 0;
For(i,1,m) {
while(top && h[stk[top]] > h[i]) {
r[stk[top]] = i - 1;
top--;
}
stk[++top] = i;
}
while(top) {
r[stk[top]] = m;
top--;
}
}
signed main() {
n = read(), m = read();
For(i,1,n) {
For(j,1,m) {
a[i][j] = read();
h[j] = (a[i][j] == 0 ? 0 : h[j] + 1);
}
work1();
work2();
For(j,1,m) {
ans = max(ans, min(h[j], r[j] - l[j] + 1));
}
}
cout << ans << '\n';
return 0;
}
3. 单调栈例题#
3.1 P2659 美丽的序列#
Problem#
给定一个长度为
Solve#
枚举所有可能的区间最小值(即每一个数),再向外扩展区间。
我们发现最终答案肯定是按区间长度单调递增,所以我们要尽可能的把区间扩大。
扩大的极限就为每一个数左边第一个小于它的数的后一个数的位置与右边第一个小于它的数的前一个数的位置。
用单调栈解决即可。
Code#
#include <bits/stdc++.h>
#define int long long
#define H 19260817
#define rint register int
#define For(i,l,r) for(rint i=l;i<=r;++i)
#define FOR(i,r,l) for(rint i=r;i>=l;--i)
#define MOD 1000003
#define mod 1000000007
using namespace std;
inline int read() {
rint x=0,f=1;char ch=getchar();
while(ch<'0'||ch>'9'){if (ch=='-') f=-1;ch=getchar();}
while(ch>='0'&&ch<='9'){x=(x<<1)+(x<<3)+(ch^48);ch=getchar();}
return x*f;
}
void print(int x){
if(x<0){putchar('-');x=-x;}
if(x>9){print(x/10);putchar(x%10+'0');}
else putchar(x+'0');
return;
}
const int N = 2e6 + 10;
int n, a[N], ans, l[N], r[N], stk[N], top;
void work1() {
top = 0;
FOR(i,n,1) {
while(top && a[stk[top]] > a[i]) {
l[stk[top]] = i + 1;
top--;
}
stk[++top] = i;
}
while(top) {
l[stk[top]] = 1;
top--;
}
}
void work2() {
top = 0;
For(i,1,n) {
while(top && a[stk[top]] > a[i]) {
r[stk[top]] = i - 1;
top--;
}
stk[++top] = i;
}
while(top) {
r[stk[top]] = n;
top--;
}
}
signed main() {
n = read();
For(i,1,n) a[i] = read();
work1();
work2();
For(i,1,n) {
ans = max(ans, 1ll * a[i] * (r[i] - l[i] + 1));
}
cout << ans << '\n';
return 0;
}
3.2 P1901 发射站#
Problem#
给定
Solve#
一眼单调栈。
建一个单调递减的栈,分别从左往右扫,从右往左扫找到每一个能量站向左/右看第一个大于此能量站高度的能量站,并把大于此能量站高度的能量站的能量加到此能量站里去。
时间复杂度
Code#
#include <bits/stdc++.h>
#define ll long long
#define H 19260817
#define rint register int
#define For(i,l,r) for(rint i=l;i<=r;++i)
#define FOR(i,r,l) for(rint i=r;i>=l;--i)
#define MOD 1000003
#define mod 1000000007
using namespace std;
inline int read() {
rint x=0,f=1;char ch=getchar();
while(ch<'0'||ch>'9'){if (ch=='-') f=-1;ch=getchar();}
while(ch>='0'&&ch<='9'){x=(x<<1)+(x<<3)+(ch^48);ch=getchar();}
return x*f;
}
void print(int x){
if(x<0){putchar('-');x=-x;}
if(x>9){print(x/10);putchar(x%10+'0');}
else putchar(x+'0');
return;
}
const int N = 1e6 + 10;
int n, l[N], r[N], ans, h[N], v[N], stk[N], top;
signed main() {
n = read();
For(i,1,n) h[i] = read(), v[i] = read();
top = 0;
For(i,1,n) {
while(top && h[stk[top]] < h[i]) {
r[i] += v[stk[top]];
--top;
}
stk[++top] = i;
}
top = 0;
FOR(i,n,1) {
while(top && h[stk[top]] < h[i]) {
l[i] += v[stk[top]];
--top;
}
stk[++top] = i;
}
For(i,1,n) ans = max(ans, l[i] + r[i]);
cout << ans << '\n';
return 0;
}
3.3 P1950 长方形#
Problem#
给定一个
问有多少个不同的由‘.’组成的矩形(“不同”当且仅当矩形的大小与位置均不相同)
Solve#
暴力很难做,需要用到降为技巧。
类比于 2.1.1 最大正方形 那道题,这道题与之类似,都可以用到悬线法。
分别建一个单调递增和单调不递减的栈,然后遍历每一行,记录从这一行向上看‘.’的个数。然后做与 2.1.1 最大正方形 同样的操作即可。
注意这里记录
Code#
#include <bits/stdc++.h>
#define int long long
#define H 19260817
#define rint register int
#define For(i,l,r) for(rint i=l;i<=r;++i)
#define FOR(i,r,l) for(rint i=r;i>=l;--i)
#define MOD 1000003
#define mod 1000000007
using namespace std;
inline int read() {
rint x=0,f=1;char ch=getchar();
while(ch<'0'||ch>'9'){if (ch=='-') f=-1;ch=getchar();}
while(ch>='0'&&ch<='9'){x=(x<<1)+(x<<3)+(ch^48);ch=getchar();}
return x*f;
}
void print(int x){
if(x<0){putchar('-');x=-x;}
if(x>9){print(x/10);putchar(x%10+'0');}
else putchar(x+'0');
return;
}
const int N = 1e3 + 10;
int n, m, h[N], stk[N], l[N], r[N], top, ans;
char c[N][N];
void stkl() {
top = 0;
FOR(i,m,1) {
while(top && h[stk[top]] >= h[i]) {
l[stk[top]] = i+1;
top--;
}
stk[++top] = i;
}
while(top) {
l[stk[top]] = 1;
top--;
}
}
void stkr() {
top = 0;
For(i,1,m) {
while(top && h[stk[top]] > h[i]) {
r[stk[top]] = i-1;
top--;
}
stk[++top] = i;
}
while(top) {
r[stk[top]] = m;
top--;
}
}
signed main() {
n = read(), m = read();
For(i,1,n) For(j,1,m) cin >> c[i][j];
For(i,1,n) {
For(j,1,m) {
if(c[i][j] == '.') h[j]++;
else h[j] = 0;
}
stkl();
stkr();
For(j,1,m) {
ans += (j - l[j] + 1) * (r[j] - j + 1) * h[j];
}
}
cout << ans << '\n';
return 0;
}
3.4 P3467 [POI2008] PLA-Postering#
Problem#
给定
Solve#
容易发现,由于覆盖的矩形长宽任意,所以被覆盖的矩形的宽是没有用的。
对于
所以建一个单调递增的栈,遇到于栈顶相同的元素,就记录一下。
时间复杂度
Code#
#include <bits/stdc++.h>
#define ll long long
#define H 19260817
#define rint register int
#define For(i,l,r) for(rint i=l;i<=r;++i)
#define FOR(i,r,l) for(rint i=r;i>=l;--i)
#define MOD 1000003
#define mod 1000000007
using namespace std;
inline int read() {
rint x=0,f=1;char ch=getchar();
while(ch<'0'||ch>'9'){if (ch=='-') f=-1;ch=getchar();}
while(ch>='0'&&ch<='9'){x=(x<<1)+(x<<3)+(ch^48);ch=getchar();}
return x*f;
}
void print(int x){
if(x<0){putchar('-');x=-x;}
if(x>9){print(x/10);putchar(x%10+'0');}
else putchar(x+'0');
return;
}
const int N = 2e6 + 5e5 + 10;
int n, h[N], stk[N], top, ans, x;
signed main() {
n = read();
For(i,1,n) x = read(), h[i] = read();
For(i,1,n) {
while(top && h[stk[top]] >= h[i]) {
if(h[i] == h[stk[top]]) ans++;
top--;
}
stk[++top] = i;
}
cout << n - ans << '\n';
return 0;
}
3.5 CF1691D Max GEQ Sum#
Problem#
给定一个长度为
Solve#
转换一下角度:要求
暴力可以做到了
换一种思路,枚举每个数作为最大值的区间,把区间分成左右两段,分别进行单调栈即可。
设
要是命题成立,则要满足:
时间复杂度
Code#
#include <bits/stdc++.h>
#define int long long
#define H 19260817
#define rint register int
#define For(i,l,r) for(rint i=l;i<=r;++i)
#define FOR(i,r,l) for(rint i=r;i>=l;--i)
#define MOD 1000003
#define mod 1000000007
using namespace std;
inline int read() {
rint x=0,f=1;char ch=getchar();
while(ch<'0'||ch>'9'){if (ch=='-') f=-1;ch=getchar();}
while(ch>='0'&&ch<='9'){x=(x<<1)+(x<<3)+(ch^48);ch=getchar();}
return x*f;
}
void print(int x){
if(x<0){putchar('-');x=-x;}
if(x>9){print(x/10);putchar(x%10+'0');}
else putchar(x+'0');
return;
}
const int N = 2e5 + 10;
int T, n, a[N], sum[N], pre[N], stk[N], top, f;
signed main() {
T = read();
while(T--) {
n = read();
For(i,1,n) a[i] = read();
// cout << "Tes" << '\n';
For(i,1,n) sum[i] = sum[i - 1] + a[i];
FOR(i,n,1) pre[i] = pre[i + 1] + a[i];
top = 0;
f = 0;
For(i,1,n) {
int maxi = 0;
while(top && a[stk[top]] <= a[i]) {
maxi = max(maxi, sum[i-1] - sum[stk[top]-1]);
top--;
}
if (maxi > 0) {
f = 1; break;
}
stk[++top] = i;
}
top = 0;
FOR(i,n,1) {
int maxi = 0;
while(top && a[stk[top]] <= a[i]) {
maxi = max(maxi, pre[i+1] - pre[stk[top]+1]);
top--;
}
if (maxi > 0) {
f = 1; break;
}
stk[++top] = i;
}
if(f) puts("NO");
else puts("YES");
}
return 0;
}
4. 单调队列#
4.1 什么是单调队列#
单调队列又称滑动窗口算法,它可以在
同样可以理解为有 淘汰性质 的单调栈。(本质就是单调栈 + 时间戳)。
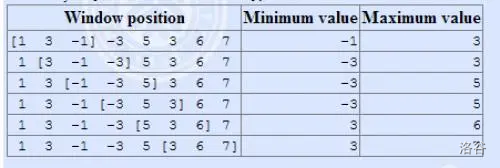
什么是固定长度的所有区间最大/最小值呢?
请看下图:
4.2 算法流程#
4.2.1 luoguP1886 滑动窗口 /【模板】单调队列#
有一个长为
【数据范围】
对于
对于
4.2.2 Solve#
把样例贺过来,以最大值为例,建一个单调递减的单调队列。
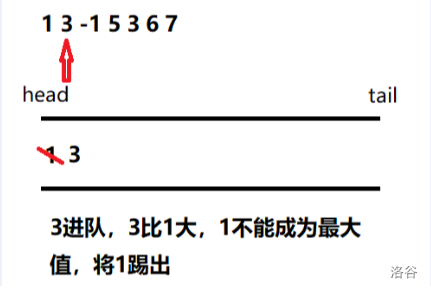
No.1
No.2
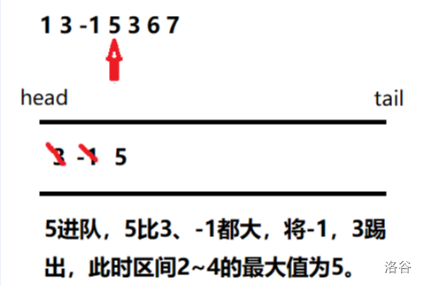
No.3
No.4
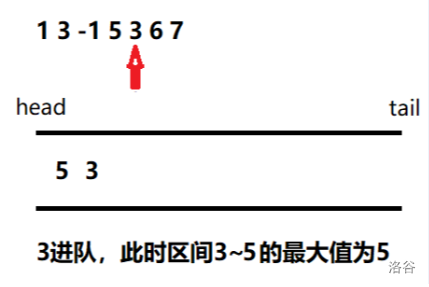
No.5
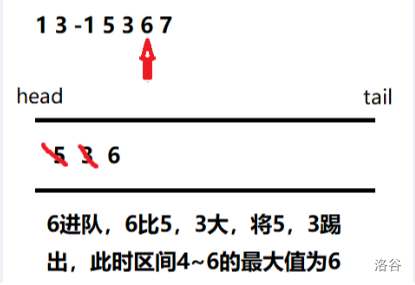
No.6
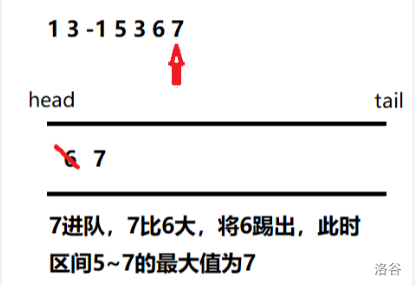
No.7
值得注意的是,要是某个元素过期了(过了所求区间),就要将其从 head 弹出。
4.2.3 Code#
#include <bits/stdc++.h>
#define ll long long
#define H 19260817
#define rint register int
#define For(i,l,r) for(rint i=l;i<=r;++i)
#define FOR(i,r,l) for(rint i=r;i>=l;--i)
#define MOD 1000003
#define mod 1000000007
using namespace std;
inline int read() {
rint x=0,f=1;char ch=getchar();
while(ch<'0'||ch>'9'){if (ch=='-') f=-1;ch=getchar();}
while(ch>='0'&&ch<='9'){x=(x<<1)+(x<<3)+(ch^48);ch=getchar();}
return x*f;
}
void print(int x){
if(x<0){putchar('-');x=-x;}
if(x>9){print(x/10);putchar(x%10+'0');}
else putchar(x+'0');
return;
}
const int N = 1000100;
int n, k, a[N], q[N], h = 1, t = 0;
signed main() {
n = read(), k = read();
For(i,1,n) a[i] = read();
For(i,1,n) {
while(h <= t && i - q[h] + 1 > k) h++;
while(h <= t && a[q[t]] > a[i]) t--;
q[++t] = i;
if(i >= k) cout << a[q[h]] << ' ';
}
h = 1, t = 0;
cout << '\n';
For(i,1,n) {
while(h <= t && i - q[h] + 1 > k) h++;
while(h <= t && a[q[t]] < a[i]) t--;
q[++t] = i;
if(i >= k) cout << a[q[h]] << ' ';
}
return 0;
}
4.3 单调队列时间复杂度分析#
和单调栈一样,每个元素最多会进队出队一次。所以时间复杂度为
5. 单调队列例题#
5.1 P2698 [USACO12MAR] Flowerpot S#
Problem#
给定
每滴水以每秒
求最小的花盆的宽度
Solve#
考虑二分答案,由于花盆的宽度与合法的概率有单调性,所以直接二分花盆宽度
check 的时候用一个单调队列记录窗口长度为
Code#
#include <bits/stdc++.h>
#define ll long long
#define H 19260817
#define rint register int
#define For(i,l,r) for(rint i=l;i<=r;++i)
#define FOR(i,r,l) for(rint i=r;i>=l;--i)
#define MOD 1000003
#define mod 1000000007
using namespace std;
inline int read() {
rint x=0,f=1;char ch=getchar();
while(ch<'0'||ch>'9'){if (ch=='-') f=-1;ch=getchar();}
while(ch>='0'&&ch<='9'){x=(x<<1)+(x<<3)+(ch^48);ch=getchar();}
return x*f;
}
void print(int x){
if(x<0){putchar('-');x=-x;}
if(x>9){print(x/10);putchar(x%10+'0');}
else putchar(x+'0');
return;
}
const int N = 100100;
struct Node {
int x, y;
}a[N];
int n = read(), D = read(), w, l = 1, r = 1;
int q1[N], q2[N];
bool cmp(Node x, Node y) {
return x.x < y.x;
}
bool check(int k) {
int h1 = 1, t1 = 0, h2 = 1, t2 = 0;
For(i,1,n) {
while(h1 <= t1 && a[i].x - a[q1[h1]].x > k) h1++;
while(h2 <= t2 && a[i].x - a[q2[h2]].x > k) h2++;
while(h1 <= t1 && a[q1[t1]].y < a[i].y) t1--;
while(h2 <= t2 && a[q2[t2]].y > a[i].y) t2--;
q1[++t1] = q2[++t2] = i;
if(a[q1[h1]].y - a[q2[h2]].y >= D) return 1;
}
return 0;
}
signed main() {
For(i,1,n) {
int p;
a[i] = (Node){read(), p = read()};
r = max(r, p);
}
sort(a + 1, a + n + 1, cmp);
w = -1;
while(l <= r) {
int mid = l + r >> 1;
if(check(mid)) {
w = mid;
r = mid - 1;
} else {
l = mid + 1;
}
}
cout << w << '\n';
return 0;
}
5.2 P2216 [HAOI2007] 理想的正方形#
Problem#
给定一个
Solve#
这道题是二维单调队列模板,但是很考察代码实现能力。
先对每一行求一边窗口长度为
Code#
#include <bits/stdc++.h>
#define int long long
#define H 19260817
#define rint register int
#define For(i,l,r) for(rint i=l;i<=r;++i)
#define FOR(i,r,l) for(rint i=r;i>=l;--i)
#define MOD 1000003
#define mod 1000000007
using namespace std;
inline int read() {
rint x=0,f=1;char ch=getchar();
while(ch<'0'||ch>'9'){if (ch=='-') f=-1;ch=getchar();}
while(ch>='0'&&ch<='9'){x=(x<<1)+(x<<3)+(ch^48);ch=getchar();}
return x*f;
}
void print(int x){
if(x<0){putchar('-');x=-x;}
if(x>9){print(x/10);putchar(x%10+'0');}
else putchar(x+'0');
return;
}
const int N = 1e3 + 10;
int a, b, n, q[N], mp[N][N], lineMAX[N][N], lineMIN[N][N], zongMAX[N][N], zongMIN[N][N], ans = LLONG_MAX;
signed main() {
a = read(), b = read(), n = read();
For(i,1,a) For(j,1,b) mp[i][j] = read();
For(i,1,a) {
int h = 1, t = 0;
For(j,1,b) {
while(h <= t && j - q[h] + 1 > n) h++;
while(h <= t && mp[i][q[t]] < mp[i][j]) t--;
q[++t] = j;
if(j >= n) lineMAX[i][j] = mp[i][q[h]];
}
h = 1, t = 0;
For(j,1,b) {
while(h <= t && j - q[h] + 1 > n) h++;
while(h <= t && mp[i][q[t]] > mp[i][j]) t--;
q[++t] = j;
if(j >= n) lineMIN[i][j] = mp[i][q[h]];
}
}
For(j,n,b) {
int h = 1, t = 0;
For(i,1,a) {
while(h <= t && i - q[h] + 1 > n) h++;
while(h <= t && lineMAX[q[t]][j] < lineMAX[i][j]) t--;
q[++t] = i;
if(i >= n) zongMAX[i][j] = lineMAX[q[h]][j];
}
h = 1, t = 0;
For(i,1,a) {
while(h <= t && i - q[h] + 1 > n) h++;
while(h <= t && lineMIN[q[t]][j] > lineMIN[i][j]) t--;
q[++t] = i;
if(i >= n) zongMIN[i][j] = lineMIN[q[h]][j];
}
}
For(i,n,a) {
For(j,n,b) ans = min(ans, zongMAX[i][j] - zongMIN[i][j]);
}
cout << ans << '\n';
return 0;
}
作者:Daniel-yao
出处:https://www.cnblogs.com/Daniel-yao/p/17053656.html
版权:本作品采用「署名-非商业性使用-相同方式共享 4.0 国际」许可协议进行许可。


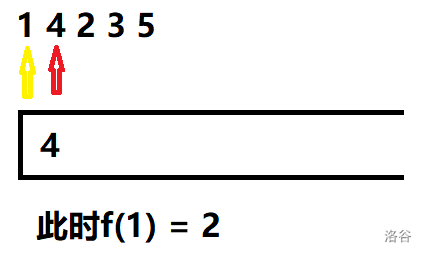






【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 地球OL攻略 —— 某应届生求职总结
· 周边上新:园子的第一款马克杯温暖上架
· Open-Sora 2.0 重磅开源!
· 提示词工程——AI应用必不可少的技术
· .NET周刊【3月第1期 2025-03-02】