【算法】线段树
1. 线段树简介
1.1 前言
线段树是一个很重要的数据结构，线段树主要用于优化时间复杂度或处理一些较灵活的问题。本文会注重介绍线段树的基础用法。
1.2 什么是线段树？
线段树是一种特殊的二叉树，其特殊在于每个节点都管辖着一个区间。线段树可以将一段区间划分成一些单元区间，每个单元区间对应线段树中的一个叶结点。
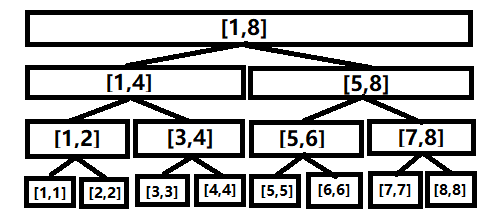
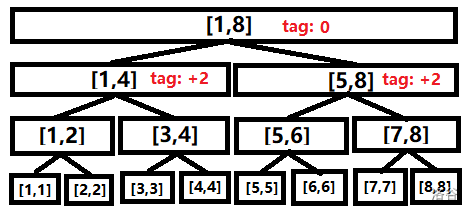
下图就是一个典型的线段树：
（请记住这张图，讲线段树的基本操作的时候会用到！）
我们可以利用线段树进行一些区间操作。
住：以下内容均以区间和为例。
1.3 建树
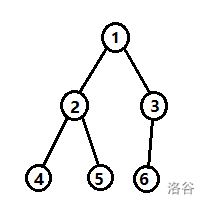
学过二叉树的同学都知道，有一种二叉树的存储方法就是【顺序存储】。
如下图
\(1\) 号节点有两个儿子，编号为 \(2\)、\(3\)。
\(2\) 号节点也有两个儿子，编号为 \(4\)、\(5\)。
\(3\) 号节点只有一个儿子，编号为 \(6\)。
根据分类，我们可以把一个节点的儿子分为左儿子和右儿子，设父节点的编号为 \(x\)，则左儿子的节点编号为 \(2x\)，右儿子的节点编号为 \(2x+1\)。线段树亦是如此。
在 1.2 中提到了"线段树可以将一段区间划分成一些单元区间"，观察发现，若父节点所管辖的区间为 \([l,r]\)，则左儿子所管辖的区间为 \([l,mid]\)，右儿子所管辖的区间为 \([mid+1,r]\)。
前置内容都讲完了，正式切入正题：如何建树？
用结构体存储节点的信息，包括节点管辖的区间 \([l,r]\)，节点信息，\(lazy\) 标记（用于区间修改，留个悬念）。
考虑递归建树，每次将区间分为两部分（即 \([l,mid]\) 和 \([mid+1,r]\)）。分配给左右儿子，再分别进入左右儿子。若递归到叶节点（即节点所管辖的区间 \(l = r\)），直接将叶节点的信息改为想要维护的信息，重复上述过程直至结束。
回溯时记得要把信息合并。
具体实现见代码：
struct Segment_Tree {
int l, r;
int num;
int tag;
}t[N << 2];
void pushup(int p) {
t[p].num = t[p << 1].num + t[p << 1 | 1].num;
}
void build(int p, int l, int r) {
t[p].l = l, t[p].r = r;
if(l == r) {
t[p].num = a[l]; return ;
}
int mid = l + r >> 1;
build(p << 1, l, mid);
build(p << 1 | 1, mid + 1, r);
pushup(p);
}
\(pushup\) 函数是将子节点的信息上传至父节点的过程（又称信息合并）。
建树时，build(1, 1, n) 就行了。
1.4 区间查询
运用了二分 + 分块的思想。
假设要查 \([3,7]\)，则可把其分为 \([3,4]\)、\([5,6]\) 和 \([7,7]\) 来求解。
如下图：
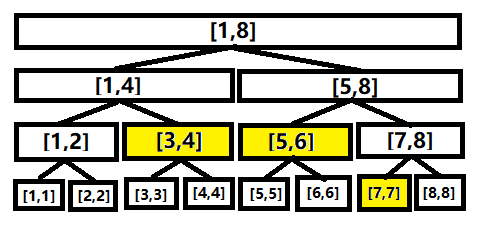
ps：黄颜色的点即是被查询的点
这样，我们便可以用 \(O(\log_2n)\) 的时间复杂度来解决区间查询问题。
具体实现见代码：
int query(int p, int l, int r) {
if(l <= t[p].l && t[p].r <= r) {
return t[p].num;
}
int ans = 0, mid = t[p].l + t[p].r >> 1;
if(l <= mid) {
ans += query(p << 1, l, r);
}
if(r > mid) {
ans += query(p << 1 | 1, l, r);
}
return ans;
}
单点查询其实就是区间查询的子集，当查询单点 \(l\) 时，查询区间 \([l,l]\) 即可。
1.5 区间修改
注意！难点来了！（敲黑板
类比区间查询，我们发现区间修改需要修改叶子结点的值，也就是每次都需要跑到树的底部修改值，这样时间复杂度会退化到 \(O(n\log_2n)\)（因为当修改区间 \([1,n]\) 时，需要到 \(n\) 个叶子节点去修改值，每一次修改要花费 \(O(\log_2n)\) 的时间复杂度，总时间复杂度 \(O(n\log_2n)\)）。
那这样线段树岂不是没优势了？其实不然，只是方法没用对！
让我们集中注意力，再次类比区间查询。不难发现区间查询并非全部都停留在叶节点做查询。而是在非叶子节点。那区间修改是否能做到在非叶子节点修改呢？
为了解决此问题，这里我们就要引用 \(lazy\) 标记（也叫延迟标记） 这个东西。
每次进行区间修改时，在被修改区间所包含的节点上打一个标记，标记的内容就是"这个区间所修改的内容"，等此节点的儿子节点被查询时，再将标记下传至子节点，计算答案。
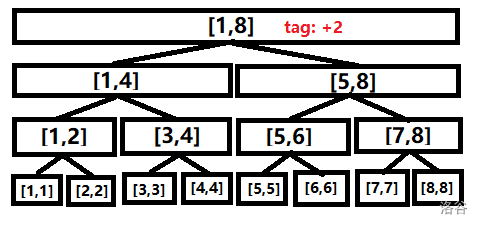
比如：将 \([1,8]\) 这段区间的值加 \(2\)，再查询区间 \([1,4]\) 便有以下过程：
1.标记"区间+2"。
2.查询时，标记下传，计算答案。
具体实现见代码：
int len(int p) {
return t[p].r - t[p].l + 1;
}
void brush(int p, int k) {
t[p].tag += k;
t[p].num += len(p) * k;
}
void pushdown(int p) {
brush(p << 1, t[p].tag);
brush(p << 1 | 1, t[p].tag);
t[p].tag = 0;
}
void add(int p, int l, int r, int k) {
if(l <= t[p].l && t[p].r <= r) {
brush(p, k);
return ;
}
pushdown(p);
int mid = t[p].l + t[p].r >> 1;
if(l <= mid) {
add(p << 1, l, r, k);
}
if(r > mid) {
add(p << 1 | 1, l, r, k);
}
pushup(p);
}
\(pushdown\) 函数是将标记下传的过程。
\(brush\)（奇怪的名字）函数是将节点打上标记的过程。
\(len\) 函数计算节点所管辖的区间的长度。
单点修改其实就是区间修改的子集，当单点修改 \(l\) 时，修改区间 \([l,l]\) 即可。
2.线段树杂项
2.1 线段树时间复杂度分析
| 操作 | 最优时间复杂度 | 最劣时间复杂度 | 常数 |
|---|---|---|---|
| 建树 | \(O(n)\) | \(O(n)\) | 大 |
| 单点修改 | \(O(\log_2 n)\) | \(O(\log_2 n)\) | 小 |
| 单点查询 | \(O(\log_2 n)\) | \(O(\log_2 n)\) | 较小 |
| 区间修改 | \(O(\log_2 n)\) | \(O(\log_2 n)\) | 大 |
| 区间查询 | \(O(\log_2 n)\) | \(O(\log_2 n)\) | 较大 |
总结：线段树固然好用，但常数异常的大，请谨慎使用！
2.2 线段树的空间
一般来讲，线段树的空间大小是数组长度的 \(4\) 倍。（一般是这样，但也有特例）
万一数组长度达到了 \(5e6\) 甚至更长，而此时又需要使用线段树时，最好的方法是：动态开点。
动态开点的精髓就在于其没有用过的点是不会占用线段树的空间的（与 vector 有异曲同工之妙），但代价就是写起来麻烦，出错了又很难调。所以不到迫不得已，不要轻易使用动态开点。
2.3 线段树的注意事项
-
很多人写线段树都没有存每一个节点所管辖的区间的习惯，而是在每一次操作时重新计算。这样既浪费时间又容易出错。建议在建树时就预处理出每一个节点所管辖的区间，并存起来。操作的时候便可以快速使用；
-
在使用线段树前记得要建树（应该不会有人忘记，毕竟建树是一个很重要也很关键的操作）；
-
有区间修改时，每一次操作（除了建树）都需要 \(pushdown\)，这样才能保证所求的区间的值是正确的；
-
\(pushdown\) 的顺序也很重要，例如：当修改、乘法和加法标记同时存在时，下传的顺序应为：先传修改，再传乘法，最后传加法。（加法和乘法之间也有一定的联系，可以参考这道题；
-
线段树的空间一定要开 4 倍！线段树的空间一定要开 4 倍！线段树的空间一定要开 4 倍！ (重要的事情说三遍)！
2.4 线段树的blogs
如果您觉得本篇 blogs 晦涩难懂，以下的几篇 blogs 是您最好的选择！！
以下是我的朋友们写的：
-
【算法】线段树 from \(Arcka\)
-
线段树学习笔记（入门） from \(sheeplittlecloud\)
(爆推！！！两位博主的其他算法总结也写得非常好！)
以下是我觉得写得不错的
3. 线段树例题
3.1 [luogu]P3372 【模板】线段树 1
Problem
已知一个数列，你需要进行下面两种操作：
- 将某区间每一个数加上 \(k\)。
- 求出某区间每一个数的和。
Solve
标准的线段树模板题
线段树的区间修改和区间查询
Code
#include <iostream>
#include <algorithm>
#include <cstring>
#include <vector>
#include <climits>
#include <map>
#include <queue>
#include <set>
#include <cmath>
#include <string>
#define int long long
#define rint register int
#define For(i,l,r) for(int i=l;i<=r;i++)
#define FOR(i,r,l) for(int i=r;i>=l;i--)
#define mod 1000000007
using namespace std;
inline int read() {
rint x=0,f=1;char ch=getchar();
while(ch<'0'||ch>'9'){if (ch=='-') f=-1;ch=getchar();}
while(ch>='0'&&ch<='9'){x=(x<<1)+(x<<3)+(ch^48);ch=getchar();}
return x*f;
}
void print(int x){
if(x<0){putchar('-');x=-x;}
if(x>9){print(x/10);putchar(x%10+'0');}
else putchar(x+'0');
return;
}
const int N = 100010;
struct Node {
int l, r;
int num;
int tag;
}t[N << 2];
int n = read(), m = read(), a[N], x, y;
int len(int p) {
return t[p].r - t[p].l + 1;
}
void brush(int p, int k) {
t[p].tag += k;
t[p].num += len(p) * k;
}
void pushdown(int p) {
brush(p << 1, t[p].tag);
brush(p << 1 | 1, t[p].tag);
t[p].tag = 0;
}
void pushup(int p) {
t[p].num = t[p << 1].num + t[p << 1 | 1].num;
}
void build(int p, int l, int r) {
t[p].l = l, t[p].r = r;
if(l == r) {
t[p].num = a[l]; return ;
}
int mid = l + r >> 1;
build(p << 1, l, mid);
build(p << 1 | 1, mid + 1, r);
pushup(p);
}
void add(int p, int l, int r, int k) {
if(l <= t[p].l && t[p].r <= r) {
brush(p, k);
return ;
}
pushdown(p);
int mid = t[p].l + t[p].r >> 1;
if(l <= mid) {
add(p << 1, l, r, k);
}
if(r > mid) {
add(p << 1 | 1, l, r, k);
}
pushup(p);
}
int query(int p, int l, int r) {
if(l <= t[p].l && t[p].r <= r) {
return t[p].num;
}
pushdown(p);
int ans = 0, mid = t[p].l + t[p].r >> 1;
if(l <= mid) {
ans += query(p << 1, l, r);
}
if(r > mid) {
ans += query(p << 1 | 1, l, r);
}
return ans;
}
signed main() {
For(i,1,n) a[i] = read();
build(1, 1, n);
For(i,1,m) {
int op, k;
op = read(), x = read(), y = read();
if(op == 1) {
k = read();
add(1, x, y, k);
} else {
print(query(1, x, y));puts("");
}
}
return 0;
}
