<leetcode c++>42.接雨水

给定 n 个非负整数表示每个宽度为 1 的柱子的高度图，计算按此排列的柱子，下雨之后能接多少雨水。

上面是由数组 [0,1,0,2,1,0,1,3,2,1,2,1] 表示的高度图，在这种情况下，可以接 6 个单位的雨水（蓝色部分表示雨水）。 感谢 Marcos 贡献此图。

示例:

输入: [0,1,0,2,1,0,1,3,2,1,2,1]
输出: 6

今天学习到了一个新的知识点，就是单调栈啦，这题保存高度单调递减的柱子下标

int trap(vector<int>& height) {
        int n=height.size();
        if(n==0)return 0;
        stack<int> idx;
        int res=0;
        for(int i=0;i<n;i++)
        {
            while(!idx.empty() && height[i] > height[idx.top()])
            {
                int cur_id = idx.top();
                idx.pop();
                while(!idx.empty() && height[cur_id]==height[idx.top()]){
                    idx.pop();
                }
                if(!idx.empty()){
                    int k=idx.top();
                    res+=(min(height[k],height[i])-height[cur_id])*(i-k-1);
                }
            }
            idx.push(i);
        }
        return res;
    }

类似的题目还有

84. 柱状图中最大的矩形

给定 n 个非负整数，用来表示柱状图中各个柱子的高度。每个柱子彼此相邻，且宽度为 1 。

求在该柱状图中，能够勾勒出来的矩形的最大面积。

 

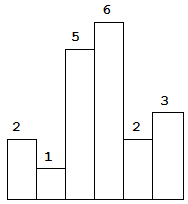
以上是柱状图的示例，其中每个柱子的宽度为 1，给定的高度为 [2,1,5,6,2,3]。

 

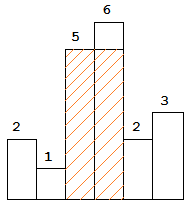
图中阴影部分为所能勾勒出的最大矩形面积，其面积为 10 个单位。

 

示例:

输入: [2,1,5,6,2,3]
输出: 10

 

保持栈内元素单调不减

int largestRectangleArea(vector<int>& heights) {
        heights.push_back(0);
        int n = heights.size();
        stack<int> idx; //保证栈内元素单调不减
        int res=0;
        for(int i=0;i<n;i++){
            while(!idx.empty() && heights[i]<=heights[idx.top()]){
                int cur_id=idx.top();idx.pop();
                res=max(res,heights[cur_id]*(idx.empty()?i:i-idx.top()-1));
            }
            idx.push(i);
        }
        return res;
    }

 

柱状图的最大矩形面积延伸到

85. 最大矩形

给定一个仅包含 0 和 1 的二维二进制矩阵，找出只包含 1 的最大矩形，并返回其面积。

示例:

输入:
[
  ["1","0","1","0","0"],
  ["1","0","1","1","1"],
  ["1","1","1","1","1"],
  ["1","0","0","1","0"]
]
输出: 6

先想到的是二分，以0划分上下左右四个矩阵，最好从中间开始找元素0，代码简洁也很好理解

int ans=0;
    void findmaxRect(vector<vector<char>>& matrix,int x,int y,int m, int n)
    {
        if(m*n<=ans)return;
        bool flag=true;
        for(int i=0;i<m;i++)
            for(int j=0;j<n;j++)
            {
                int a=(i+m/2)%m;
                int b=(j+n/2)%n;
                if(matrix[a+x][b+y]=='0')
                {
                    flag=false;
                    findmaxRect(matrix,x,y,a,n);
                    findmaxRect(matrix,x,y,m,b);
                    findmaxRect(matrix,a+x+1,y,m-a-1,n);
                    findmaxRect(matrix,x,b+y+1,m,n-b-1);
                    return;
                }
            }
        if(flag){
            ans=max(ans,m*n);
        }
    }
    int maximalRectangle(vector<vector<char>>& matrix) {
        int m=matrix.size();
        if(m==0)return 0;
        int n=matrix[0].size();
        findmaxRect(matrix,0,0,m,n);
        return ans;
    }

但是实际上可以将每列元素看作是柱状图的横向，然后求最大矩形，下面是leetcode官方题解的图：

 

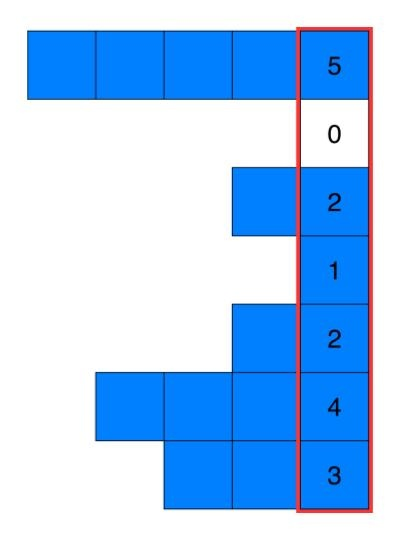
 在84题的基础上稍作修改：

int ans=0;

    void largestRectangleArea(vector<vector<char>>& matrix,int k,int m) {
        stack<int> idx; //保证栈内元素单调不减
        int res=0;
        for(int i=0;i<m;i++){
            while(!idx.empty() && matrix[i][k]<=matrix[idx.top()][k]){
                int cur_id=idx.top();idx.pop();
                res=max(res,(matrix[cur_id][k]-'0')*(idx.empty()?i:i-idx.top()-1));
            }
            idx.push(i);
        }
        ans=max(ans,res);
    }

    int maximalRectangle(vector<vector<char>>& matrix) {
        int m=matrix.size();
        if(m==0)return 0;
        int n=matrix[0].size();
        for(int i=0;i<m;i++)
            for(int j=1;j<n;j++)
            {
                if(matrix[i][j]!='0')
                    matrix[i][j]=matrix[i][j-1]+1;
            }
        vector<char> tmp(n,'0');
        matrix.push_back(tmp);
        for(int i=0;i<n;i++)
            largestRectangleArea(matrix,i,m+1);
        return ans;
    }