【Cf Edu #47 G】Allowed Letters

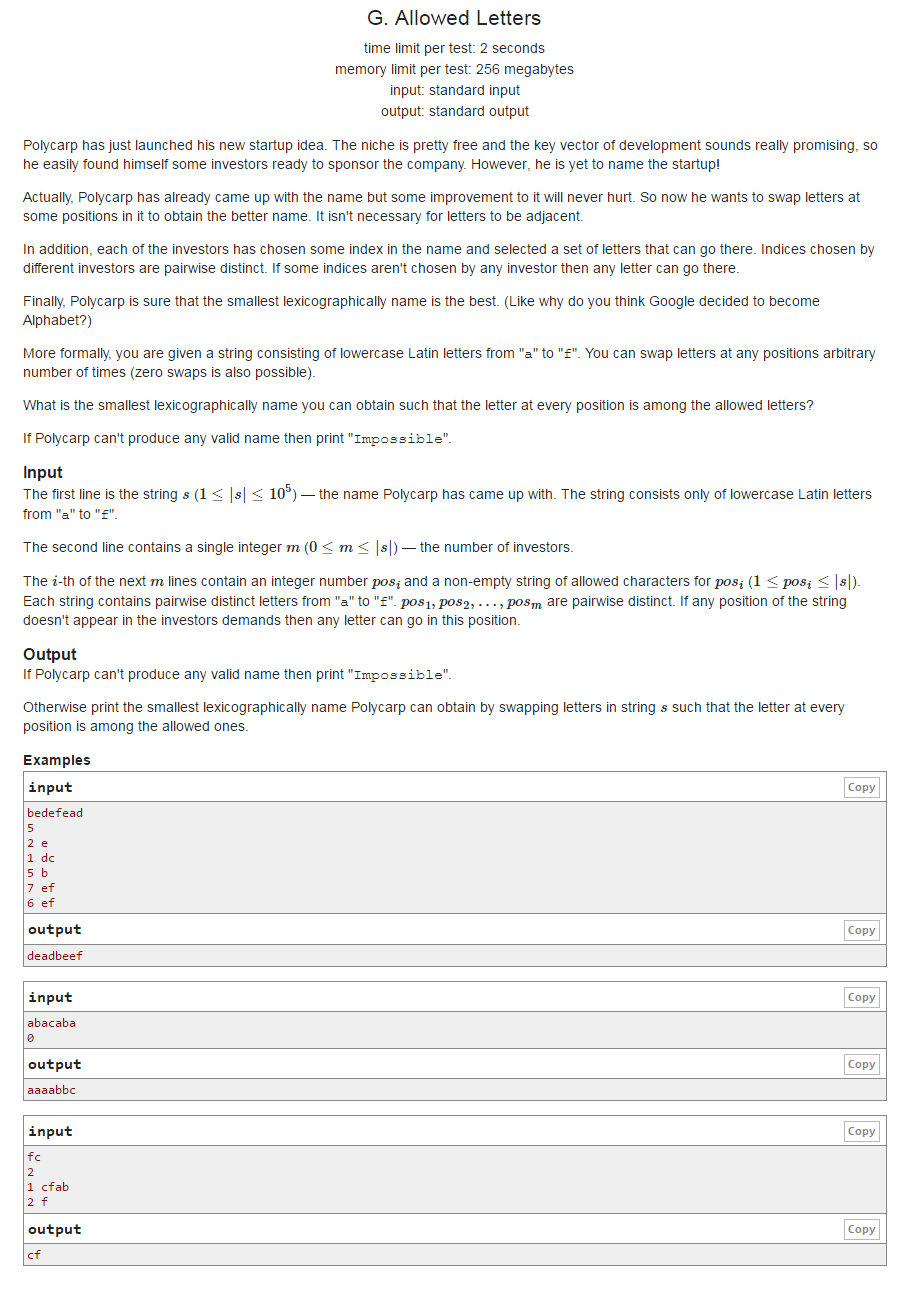
这个题大概就是每一个位置都有一个能填字符的限制（一个点集），给出已有的$n$个字符，问能填出的最小字典序的字符串。

总体思路是贪心，每一位尽量选最小的字符。

关键在于判断在某位选了一个字符后，接下来的位置能否满足限制。

考虑怎么判断有解，这里有一种网络流的思路：

1. 有$6$个点，代表了$a - f$$6$个字符，有源点向这些点连边，流量为该字符的个数。
2. 另有$2^{6}$个点，代表了各个点集，这些点向汇点连边，流量为该点集在所有限制中出现的次数。
3. 如果某个点在一个点集中，则由该点向该点集连流量为$INF$的边。

易得，当流量满流时，有合法解。

当然，用网络流这个模型虽然很容易理解，但如果每一次检验都跑一边的话效率不行，出题人有一种基于调整法的网络流做法，在已知流网络上进行修改，但是我不是很懂，代码也较长，在此不做累述。

此处所用的做法十分简洁。有以下结论：

1. 接下来仅考虑某位置选了某个字符后，判断剩下的一个后缀是否有解。
2. 定义$cnt_{i}$表示字符$i$的剩余数量，$num_{s}$表示与集合$s$有交的位置（该位置上限制的字符集与$s$有交）。
3. 枚举$2^{6}$个集合，当所有的集合都准合法时才有解。
4. 准合法的定义是：$\sum_{i = a}^{f} (其中 i \in s) <= num_{s}$。

显然，如果$|s|=1$，即$s$中只有一个字符，那$s$准合法就是$s$合法（存在合法解）。

这里用于说明$s$是合法的当且仅当所有$s$的子集是合法的，且$s$是准合法的。

由于我们从小到大枚举所有集合，可以保证所有之前已经枚举过的集合已经合法了，即它的子集都合法，故只要判断该集合是否准合法。

关于这个条件的必要性：

1. 如果$s$不是准合法的，显然$s$不会是合法的，因为没有足够位置放。
2. 如果$s$的某一个子集$s_{i}$不合法，也就是$s_{i}$的有关位置$num_{s_{i}}$不够调计，那在$s$的有关位置$num_{s}$中并不会有更多的供$s_{i}$中的字符放置的位置，那$s$也将是不合法的。

关于这个条件的充分性：

1. 如果所有它的子集都合法了，并且$s$准合法，就不会存在某一个集合中的元素占用了过多的公共位置，因为那样会导致另一个子集不合法，即产生矛盾。

这样的话就能在$O(nA2^{A})$解决问题了，其中$A$是字符集大小。

 

$\bigodot$技巧与套路：

• 利用网络流的模型
• 集合的枚举以及使用

• #include <cstdio>
  #include <cstring>
  #include <algorithm>
  
  const int N = 100005, ST = 63;
  
  int n, m, bit[N], ans[N], cnt[7], num[ST + 2][N];
  char s[N], ssr[9];
  
  inline int Check(int x) {
      for (int st = 0; st <= ST; ++st) {
          int cnum = 0;
          for (int i = 0; i < 6; ++i) {
              if ((st >> i) & 1) cnum += cnt[i];
          }
          if (num[st][n] - num[st][x] < cnum) return 0;
      }
      return 1;
  }
  
  int main() {
      scanf("%s%d", s + 1, &m);
      n = strlen(s + 1);
      for (int i = 1; i <= n; ++i) {
          bit[i] = ST; ans[i] = -1;
          ++cnt[s[i] - 'a'];
      }
      for (int i = 1, x; i <= m; ++i) {
          scanf("%d%s", &x, ssr);
          int le = strlen(ssr), st = 0;
          for (int j = 0; j < le; ++j) {
              st |= 1 << (ssr[j] - 'a');
          }
          bit[x] &= st;
      }
      
      for (int st = 0; st <= ST; ++st) {
          for (int i = 1; i <= n; ++i) {
              num[st][i] = num[st][i - 1] + (bool)(bit[i] & st);
          }
      }
      
      for (int i = 1; i <= n; ++i) {
          for (int j = 0; j < 6; ++j) {
              --cnt[j];
              if (((bit[i] >> j) & 1) && Check(i)) {
                  ans[i] = j; break;
              }
              ++cnt[j];
          }
          if (ans[i] == -1) {
              puts("Impossible");
              return 0;
          }
      }
      for (int i = 1; i <= n; ++i) {
          putchar(ans[i] + 'a');
      }
      
      return 0;
  }