【科技】高斯消元简析

想必大家都可以非常迅速的解出一个二元一次方程组，

那么三元呢（这也还好），那么再多一些未知数？

于是这里就要介绍到高斯消元的方法了...

本人蒟蒻到现在才学高斯消元，请不要介意方法过于垃圾

 --------------------------------------------------------------------------------------------------

首先假设你拿到了一个n元方程组，那么它应该有n个方程，每个方程有n+1个系数，

好于是我们把他们全部弄到一个n*(n+1)的矩阵中，这里简称为系数矩阵

第一步：我们先把每一行的系数都除以这一行的第一个数

第二步：从第一行到第n行分别控制x1...xn的解，因此你需要把第i行的第i列的系数化为1以此来求解方程，

第三步：在处理第i行的时候，把第i+1行到第n行的数通过加减消元法处理

   

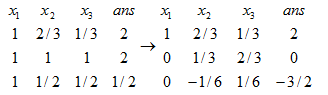
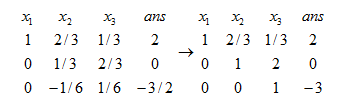
第四步：那么求出这个答案就是最后的答案数组了，

求答案是xn的值是a[n][n+1]，然后如果求x(n-1)的值就是将xn的值代入a[n-1][n]，然后求出x(n-1)的值

于是乎 x1=-1，x2=3，x3=-6

以上就是关于高斯消元简要的介绍.

 

以下是高斯消元实数的模板，在无解时返回1。

bool Gauss(){
    for (int i=0;i<n;++i){
        int k=i;
        for (int j=i+1;j<n;++j) if (a[j][i] > a[k][i]) k=j;
        now=a[k][i];
        if (now==0) return 1;
        for (int j=i;j<=n;++j) swap(a[i][j],a[k][j]);
        for (int j=i;j<=n;++j) a[i][j]=Mul(a[i][j],Inv(now));
        for (k=0;k<n;++k) if (k!=i){
            now=a[k][i];
            for (int j=i;j<=n;++j) MO(a[k][j]-=Mul(a[i][j],now));
        }
    }return 0;
}