【CF edu 30 D. Merge Sort】
time limit per test 2 seconds
memory limit per test 256 megabytes
input standard input
output standard output
Merge sort is a well-known sorting algorithm. The main function that sorts the elements of array a with indices from [l, r) can be implemented as follows:
- If the segment [l, r) is already sorted in non-descending order (that is, for any i such that l ≤ i < r - 1 a[i] ≤ a[i + 1]), then end the function call;
- Let
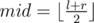 ;
; - Call mergesort(a, l, mid);
- Call mergesort(a, mid, r);
- Merge segments [l, mid) and [mid, r), making the segment [l, r) sorted in non-descending order. The merge algorithm doesn't call any other functions.
The array in this problem is 0-indexed, so to sort the whole array, you need to call mergesort(a, 0, n).
The number of calls of function mergesort is very important, so Ivan has decided to calculate it while sorting the array. For example, ifa = {1, 2, 3, 4}, then there will be 1 call of mergesort — mergesort(0, 4), which will check that the array is sorted and then end. Ifa = {2, 1, 3}, then the number of calls is 3: first of all, you call mergesort(0, 3), which then sets mid = 1 and calls mergesort(0, 1)and mergesort(1, 3), which do not perform any recursive calls because segments (0, 1) and (1, 3) are sorted.
Ivan has implemented the program that counts the number of mergesort calls, but now he needs to test it. To do this, he needs to find an array a such that a is a permutation of size n (that is, the number of elements in a is n, and every integer number from [1, n] can be found in this array), and the number of mergesort calls when sorting the array is exactly k.
Help Ivan to find an array he wants!
Input
The first line contains two numbers n and k (1 ≤ n ≤ 100000, 1 ≤ k ≤ 200000) — the size of a desired permutation and the number ofmergesort calls required to sort it.
Output
If a permutation of size n such that there will be exactly k calls of mergesort while sorting it doesn't exist, output - 1. Otherwise output ninteger numbers a[0], a[1], ..., a[n - 1] — the elements of a permutation that would meet the required conditions. If there are multiple answers, print any of them.
Examples
input
3 3
output
2 1 3
input
4 1
output
1 2 3 4
input
5 6
output
-1
【翻译】将一个数组进行归并排序(升序),递归区间左闭右开,总区间为[0,n),M=l+r>>1。如果地柜的时候当前的区间已经有序(升序),则不能继续调用函数MergeSort(l,M)和MergeSort(M,r)。输入一个k,要求构造一个序列,满足将其归并排序的函数调用次数恰好为n,输出这个序列。
题解:
①如果一个区间没有排好序,那么会调用左右两个区间,操作数+2
②因此如果能够构成k,那么首先k一定为奇数(2*x+1,1表示调用MergeSort(0,n))
③由于每次会加+2,因此直接递归并且交换当前的a[M-1],a[M]。
④每次人为地让区间无序,并且cnt+=2。
⑤如果能够满足cnt>=k,那么一定存在解。否则输出-1.
#include<stdio.h>
#include<algorithm>
#define go(i,a,b) for(int i=a;i<=b;i++)
const int N=200003;
int n,k,a[N],tot;
void Divide_And_Conquer(int l,int r)
{
if(l+1==r||tot==k)return;
int M=l+r>>1;tot+=2;
a[M-1]^=a[M]^=a[M-1]^=a[M];
Divide_And_Conquer(l,M);
Divide_And_Conquer(M,r);
}
int main()
{
scanf("%d%d",&n,&k);k--;
if(k&1){puts("-1");return 0;}
go(i,0,n-1)a[i]=i+1;Divide_And_Conquer(0,n);
if(tot<k){puts("-1");return 0;};
go(i,0,n-1)printf("%d ",a[i]);return 0;
}//Paul_Guderian
.


