【CF Round 439 E. The Untended Antiquity】

 

time limit per test 2 seconds

memory limit per test 512 megabytes

input standard input

output standard output

Adieu l'ami.

Koyomi is helping Oshino, an acquaintance of his, to take care of an open space around the abandoned Eikou Cram School building, Oshino's makeshift residence.

The space is represented by a rectangular grid of n × m cells, arranged into n rows and m columns. The c-th cell in the r-th row is denoted by (r, c).

Oshino places and removes barriers around rectangular areas of cells. Specifically, an action denoted by "1 r₁ c₁ r₂ c₂" means Oshino's placing barriers around a rectangle with two corners being (r₁, c₁) and (r₂, c₂) and sides parallel to squares sides. Similarly, "2 r₁ c₁ r₂ c₂" means Oshino's removing barriers around the rectangle. Oshino ensures that no barriers staying on the ground share any common points, nor do they intersect with boundaries of the n × m area.

Sometimes Koyomi tries to walk from one cell to another carefully without striding over barriers, in order to avoid damaging various items on the ground. "3 r₁ c₁ r₂ c₂" means that Koyomi tries to walk from (r₁, c₁) to (r₂, c₂) without crossing barriers.

And you're here to tell Koyomi the feasibility of each of his attempts.

Input

The first line of input contains three space-separated integers n, m and q (1 ≤ n, m ≤ 2 500, 1 ≤ q ≤ 100 000) — the number of rows and columns in the grid, and the total number of Oshino and Koyomi's actions, respectively.

The following q lines each describes an action, containing five space-separated integers t, r₁, c₁, r₂, c₂ (1 ≤ t ≤ 3, 1 ≤ r₁, r₂ ≤ n, 1 ≤ c₁, c₂ ≤ m) — the type and two coordinates of an action. Additionally, the following holds depending on the value of t:

• If t = 1: 2 ≤ r₁ ≤ r₂ ≤ n - 1, 2 ≤ c₁ ≤ c₂ ≤ m - 1;
• If t = 2: 2 ≤ r₁ ≤ r₂ ≤ n - 1, 2 ≤ c₁ ≤ c₂ ≤ m - 1, the specified group of barriers exist on the ground before the removal.
• If t = 3: no extra restrictions.

Output

For each of Koyomi's attempts (actions with t = 3), output one line — containing "Yes" (without quotes) if it's feasible, and "No" (without quotes) otherwise.

Examples

input

5 6 5
1 2 2 4 5
1 3 3 3 3
3 4 4 1 1
2 2 2 4 5
3 1 1 4 4

output

No
Yes

input

2500 2500 8
1 549 1279 1263 2189
1 303 795 1888 2432
1 2227 622 2418 1161
3 771 2492 1335 1433
1 2017 2100 2408 2160
3 48 60 798 729
1 347 708 1868 792
3 1940 2080 377 1546

output

No
Yes
No

Note

For the first example, the situations of Koyomi's actions are illustrated below.

 

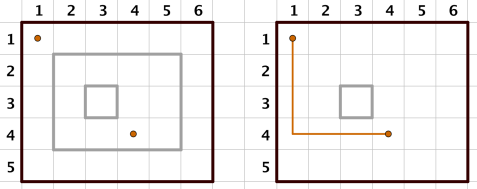
【翻译】给出n*m的方格纸，现在q个操作，1表示将给定矩形加上一圈墙，2表示删除给定矩形的墙(保证之前有墙),3表示询问两点是否能够到达。

 

题解：

   ①题目说，围墙不会重合，所以只要两个点在同一个墙内或者不在任何墙内，就可以通达。

   ②因此可以标记墙内所有点，给它们涂上一个颜色，然后维护一个差分，可以计算是否在墙内。

   ③颜色可以使用哈希值表示，对于查分使用二维树状数组维护。

#include<stdio.h>
#define base 4050
#define M 10000007
#define go(i,a,b) for(int i=a;i<=b;i++)
int n,m,q,x1,y1,x2,y2,t,c[2503][2503];
int Get_Hash()
{
	long long a=0;
	a=(a*base+x1)%M;a=(a*base+y1)%M;
	a=(a*base+x2)%M;a=(a*base+y2)%M;
	return (int)(a%M+M)%M;
}
void Add(int x,int y,int d)
{
	int i=x;while(i<=n){
	int j=y;while(j<=m)c[i][j]+=d,j+=j&-j;i+=i&-i;}
}
int Sum(int x,int y,int R=0)
{
	int i=x;while(i){
	int j=y;while(j)R+=c[i][j],j-=j&-j;i-=i&-i;}return R;
}
void Update(int val)
{
	Add(x1,y1,val);
	Add(x1,y2+1,-val);
	Add(x2+1,y1,-val);	
	Add(x2+1,y2+1,val);
}
int main()
{	
	scanf("%d%d%d",&n,&m,&q);
	while(q--&&scanf("%d%d%d%d%d",&t,&x1,&y1,&x2,&y2))
	{
		if(t==1)Update(+Get_Hash());
		if(t==2)Update(-Get_Hash());		
		if(t==3)puts(Sum(x1,y1)==Sum(x2,y2)?"Yes":"No");
	}
	return 0;
}//Paul_Guderian

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

我听到无声的悲泣，回荡在心碎的恩赐之地，

闪烁的灯映着那忧伤的少年。——————汪峰《恩赐之地》