PKUSC2024 题解
\(\text{By DaiRuiChen007}\)
D1T1. 回文路径
给定 \(2\times n\) 网格,每个格子上有一个字符,考虑一条只能向下和向右走的路径,如果路径上每个字符连成的字符串是回文串,称这条路径是好的,求最长好路径。
数据范围:\(n\le 10^5\)
枚举回文中心,不妨设其在第一行,那么二分出在只在第一行能走到的最长距离,然后在右端点向下走一步,再二分在第二行能移动到最长距离。
可以用哈希快速判断路径是否回文。
时间复杂度 \(\mathcal O(n)\)。
D1T2. 正方形计数
给定凸 \(n\) 边形 \((x_1,y_1)\sim(x_n,y_n)\),求有多少正方形(可以是斜正方形)在该多边形内。
数据范围:\(n\le 8,x_i,y_i\le 2000\)。
考虑枚举正方形的一条边向量 \((\Delta x,\Delta y)\),然后对起点坐标有若干限制,可以写成半平面交的形式。
相当于数某个多边形内部整点数,可以拆成对 \(\mathcal O(n)\) 条线段下方的区域内数点个数,类欧几里得算法解决。
时间复杂度 \(\mathcal O(nV^2\log V)\)。
暴力能过,没写正解。
D1T3. 独立
给定 \(n\) 个点的树,每个点点权在 \([1,m]\) 中随机,求所有方案下树上最大权独立集的和。
数据范围:\(n\le 2000,m\le 10^{8}\)。
考虑求最大权独立集的 dp 算法:\(dp_{u,0/1}\) 表示 \(u\) 没选 / 选时的最大独立集,转移如下:
其中 \(w\) 表示权值,记 \(a_u=\max(dp_{u,0},dp_{u,1})-dp_{u,0}\),带入可得 \(a_u=\max(0,w_u-\sum_{v\in\mathrm{son}(u)}g_v)\)。
并且整棵树的最大权独立集就等于 \(\sum a_u\),因此可以根据 \(a_u\) 设计 dp 套 dp 算法。
设 \(f_{u,i}\) 表示 \(a_u=i\) 的方案数,那么转移时先求 \(g\) 为 \(f_v\) 的卷积,然后 \(f_{u,\max(j-i,0)}\gets g_i\),其中 \(j\in[1,m]\) 表示 \(w_u\)。
答案就是 \(\sum_u\sum_im^{n-siz(u)}\times i\times f_{u,i}\)。
可以写出如下 48 分暴力:Submission Link。
注意到我们要对 \(f_{u,0}\) 特殊处理,用 \(m^{siz(u)}-\sum_{i>0} f_{u,i}\) 更新,此时 \(f_{u,i}=\sum_{j=1}^{m-i} g_{j}\)。
可以用归纳法证明,对于每个 \(u\),\(f_{u,1}\sim f_{u,m}\) 是某个 \(\mathcal O(n)\) 次多项式在 \(x=1\sim m\) 处的点值。
不妨设 \(k=n+\mathcal O(1)\) 表示多项式最高次数,我们只要维护 \(f_{u,1}\sim f_{u,k}\) 即可插值出整个 \(f_u\)。
考虑如何转移,首先我们发现 \(f_{u,m-k}\sim f_{u,m}\) 是容易求的,只要求 \(g_0\sim g_k\) 即可,这个可以用 NTT 快速求出。
然后我们要考虑 \(f_{u,m-k}\sim f_{u,m}\) 通过拉格朗日插值求出 \(f_{u,1}\sim f_{u,k}\),这个也可以求出式子后用 NTT 加速。
最后我们要求 \(\sum_{i=1}^m f_{u,i}\) 来更新 \(f_{u,0}\),求 \(\sum_{i=1}^m i\times f_{u,i}\) 来更新答案,显然这两个值也是关于 \(m\) 的 \(\mathcal O(n)\) 次多项式,通过 \(f_{u,1}\sim f_{u,k}\) 来插值求答案即可。
时间复杂度 \(\mathcal O(n^2\log n)\)。
D2T1. 分流器
在一张 \(n+1\) 个点的图上,\(1\sim n\) 出度都为 \(2\),在这个图上做一个类似 Shannon 投球游戏的过程,求最小周期。
数据范围:\(n\le 50000\)。
考虑维护 \(1\sim i\) 的最小周期,并且求出此时每个点被经过的次数 \(f_{i}\)。
可以据此计算出 \(f_{i+1}=\sum_{i+1\in \mathrm{out}(u)} \dfrac{f_u}2\),如果 \(2\nmid f_{i+1}\) 那么最小周期要翻倍,每个 \(f_i\) 也 \(\times 2\)。
一个较好的实现是令 \(f_{1}=2^n\),答案就是 \(\min_{i=1}^n \mathrm{lowbit}(f_i)\),压位高精度维护。
时间复杂度 \(\mathcal O\left(\dfrac {n^2}{\omega}\right)\)。
D2T2. 排队
给定 \(n\) 个区间 \([l_i,r_i]\),定义 \(f_i(x)=x+[l_i\le x\le r_i]\),\(q\) 次询问 \(L,R\),求 \(f_R(f_{R-1}(\cdots f_{L}(0)))\)。
数据范围:\(n,q\le 10^6\)。
考虑扫描线,枚举 \(R\) 对每个 \(L\) 维护答案 \(x_L\),显然 \(x_L\) 单调不增,证明如下:
考虑 \(x_i,x_{i+1}\),若某个时刻 \(x_i=x_{i+1}\),此后所有时刻都有 \(x_i=x_{i+1}\),由于初始 \(R=i+1\) 时 \(x_i\ge x_{i+1}\),因此 \(x_{i+1}\) 不可能反超 \(x_i\)。
线段树维护所有 \(x_i\),二分出 \(x_L\in[l_i,r_i]\) 的 \(L\) 区间,区间加即可。
时间复杂度 \(\mathcal O((n+q)\log n)\)。
D2T3. 最短路径
给定纯随机的 \(n\) 个点 \(m\) 条边的带权有向图,\(q\) 次随机询问某对点 \(S\to T\) 的最短路。
数据范围:\(n\le 2\times 10^5,m\le 3\times 10^6,q\le 10^4\)。
很显然只能用一些魔改的最短路算法解决。
单向 Dijkstra 显然不太靠谱,不妨考虑双向 Dijkstra,即从起点和终点分别开始,在原图和反图上增广最短路。
设 \(S\to u\) 最短路 \(f_u\),\(u\to T\) 最短路 \(g_u\)。
两棵最短路树考虑第一次相遇的时刻,设相遇在 \(x\) 上:
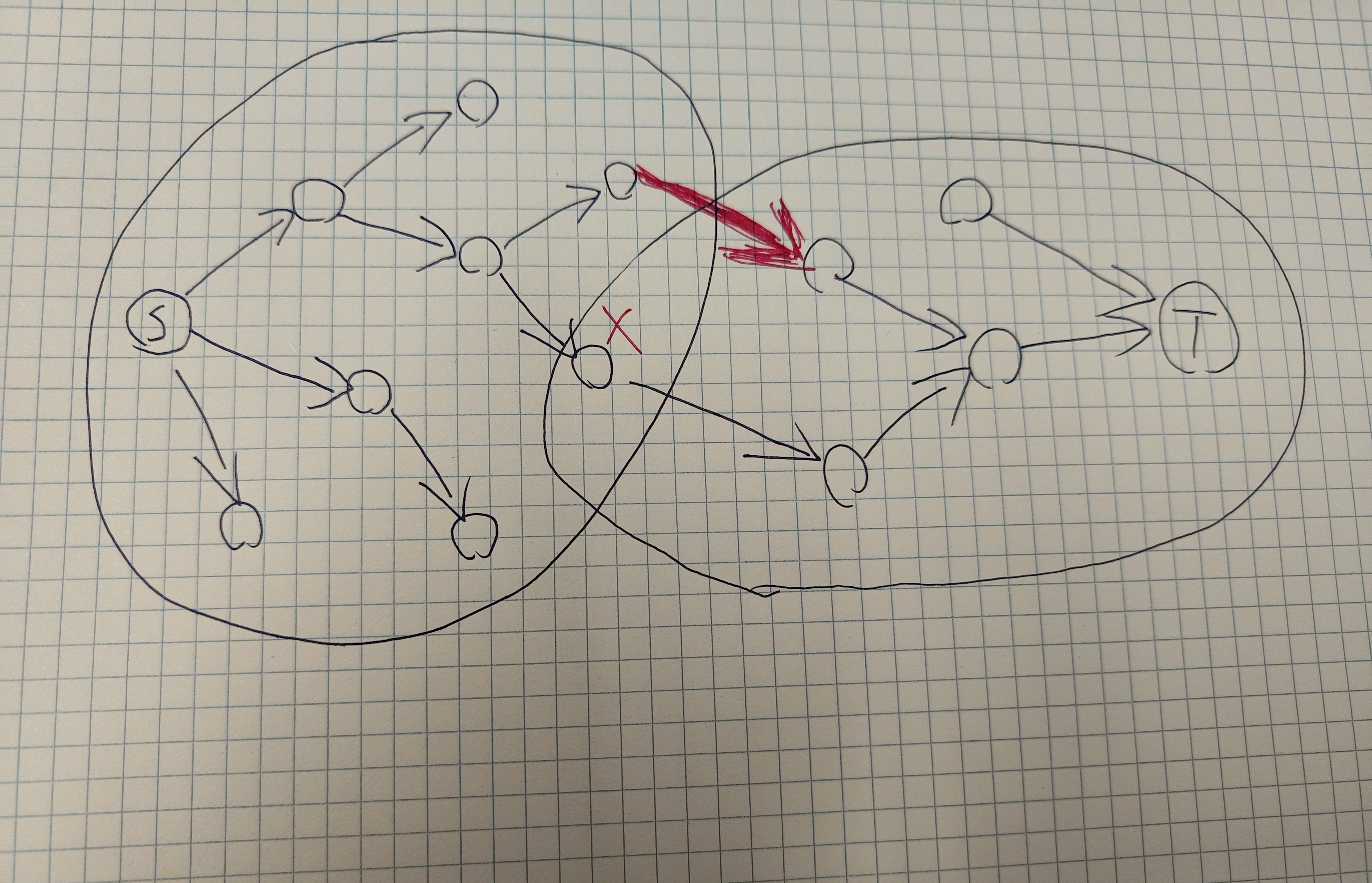
那么考虑答案的形态,首先全部经过最短路树的路径 \(f_x+g_x\) 先考虑贡献。
对于一个不全在最短路树的路径,如果这条路径经过一个最短路树外的节点 \(y\),那么 \(f_y\ge f_x,g_y\ge g_x\),这条路径肯定不优。
因此不在最短路树内的部分只可能是一条边。
然后我们分析一下最短路树的期望大小,注意到 Dijkstra 的过程中每次弹出堆顶相当于取出当前权值最小的一条边,而这条边的权值和这条边的终点没有关系,因此每次 Dijkstra 拓展到的点可以被认为是 \([1,n]\) 内均匀随机的。
所以我们每次拓展较小的一棵增广路树,根据生日悖论,期望 \(\mathcal O(\sqrt n)\) 次增广就能相遇。
但是这个复杂度并不对,因为每个点度数可能很大,增广到这个点的时候就会向堆中加入大量边。
因此我们考虑 \(k\) 短路的常用技巧,用左兄弟右儿子表示法维护这个图。
即堆中存储每一条边,增广的时候只将新节点的第一条出边入队,并且把当前边同一起点的后继边也入队。
那么这样每次增广只会加入 \(\mathcal O(1)\) 条边,入队次数和增广次数成线性。
然后考虑如何算答案,即怎样枚举所有可能的增广路树外的一条边。
对于某条边 \((u,v,w)\),其贡献为 \(f_u+g_v+w\),对答案有影响显然要求 \(f_u+g_v+w<f_x+g_x\)。
因此 \(w<(f_x-f_u)+(g_x-g_v)\le 2\max(f_x-f_u,g_x-g_v)\),我们在取到较大的一边考虑。
不妨设 \(f_x-f_u\) 较大,那么我们只关心 \(u\) 的出边中 \(<2(f_x-f_u)\) 的边,同理只关心 \(v\) 的反图出边中 \(<2(g_x-g_v)\) 的边。
对每个点出边排序后即可做到只处理合法边。
考虑分析其边数,如果 \(w< f_x-f_u\),那么这条边在 Dijkstra 过程中一定被访问过,这样的边总数是期望 \(\mathcal O(\sqrt n)\) 的。
同理,我们可以猜测 \(w<2(f_x-f_u)\) 的边也大约是 \(\mathcal O(\sqrt n)\) 量级,实际能分析出是 \(\mathcal O(\sqrt n\log n)\) 级别的。
时间复杂度 \(\mathcal O(m\log m+q\sqrt n\log n)\)。

