网络流二十四题解题报告
网络流二十四题解题报告
\(\text{By DaiRuiChen007}\)
机器人路径规划问题数据有误，不计入解题报告中
1. 飞行员配对方案问题
构造二分图，把每个正驾驶员当成左部点，副驾驶员当成右部点
若正驾驶员 \(a\) 和副驾驶员 \(b\) 可以同机飞行就在二分图中连边 \((a,b)\)
答案即为二分图最大匹配的大小
2. 太空飞行计划问题
考虑最大权权闭合子图，对于每个实验 \(j\) ，设点权为 \(p_j\)，对于每个器材 \(i\)，设其点权为 \(-c_i\)，并且从 \(j\) 向所有 \(i\in\mathbf R_j\) 的 \(i\) 连有向边
此时我们在闭合子图中选取实验 \(j\) 其对子图权值的贡献为 \(p_j\)，那么所有 \(\mathbf R_j\) 中的实验 \(i\) 也一定要在闭合子图中，其对子图权值的贡献为 \(-c_i\)，因此这个闭合子图的权值就是对应方案的实际收益
因此求这张图的最大权闭合子图，子图中选择的实验和器材就是最终方案里的实验和方案
3. 最小路径覆盖问题
二分图匹配解最小路径覆盖模板题，对于每条边 \(u\to v\) 在二分图中连接 \(L_u\to R_v\)，求出最大匹配 \(\mathbf M\)
每条匹配边 \(L_x\to R_y\) 相当于合并 \(x\) 所在的链和 \(y\) 所在的链，最终答案为 \(n-|\mathbf M|\)
4. 魔术球问题
首先考虑判定 \(k\) 个球能否放入 \(n\) 个柱子上，把 \(1\sim k\) 中所有和为平方数的 \((i,j)\) 求出来，设 \(i>j\)，连边 \(i\to j\)，表示 \(i\) 能放在 \(j\) 后面，求出这个图的最小路径覆盖的大小，若超过 \(n\) 就不行
我们不需要考虑二分，考虑增量算法，每次新加入一个点，然后连边判断即可，如果加入某个 \(x\) 之后不符合题意就直接 break 掉并返回 \(x-1\) 即可
注意最后输出方案的时候由于连边是从大到小的，而输出路径要求是从小到大，因此要反过来输出
5. 圆桌问题
考虑网络流做一个类似二分图匹配的过程，对国家建立节点 \(i\in[1,m]\)，餐桌建立节点 \(j\in[1,n]\)：
- 连接 \(S\to i\)，容量为 \(r_i\)，表示一个国家有 \(r_i\) 个要匹配
- 连接 \(j\to T\)，容量为 \(c_i\)，表示一个餐桌至多坐 \(c_i\) 个人
- 对于所有 \(i,j\)，连接 \(i\to j\)，容量为 \(1\)，表示 \(i\) 国家有没有一个人坐 \(j\) 号桌子
求出网络上的最大流，如果与 \(\sum r_i\) 相等则有解，输出方案时判断 \(i\to j\) 是否满流，如果满流则说明有一个人坐了桌子 \(j\)
6. 最长不下降子序列问题
第一问先 dp 求出最大长度 \(L\) 和以每个点为结尾的 LIS 长度 \(dp_i\)
因为每个点至多被选一次，因此考虑拆点，把每个点 \(i\) 拆成 \(i,i'\) 表示入和出：
- 连接 \(i\to i'\)，容量为 \(1\)，表示 \(i\) 至多使用一次
- 对于所有 \(dp_i=1\) 的 \(i\)，连接 \(S\to i\)，容量为 \(1\)，表示可以从 \(i\) 这个位置开始
- 对于所有 \(dp_i=L\) 的 \(i\)，连接 \(i'\to T\)，容量为 \(1\)，表示可以从 \(i\) 这个位置结束
- 对于所有在 dp 过程中能从 \(j\) 转移到 \(i\) 的 \((j,i)\)，连接 \(j'\to i\)，容量为 \(1\)，表示 \(i\) 在子序列中可以接在 \(j\) 的后面
第三问复制第二问的图，如果 \(1\) 能做起点就连接 \(S\to 1,1\to 1'\)，容量为 \(\infty\)，如果 \(n\) 能做终点就连接 \(n\to n',n'\to T\)，容量为 \(\infty\)
注意特判 \(L=1\) 的情况，此时二三问答案均为 \(n\)
7. 试题库问题
拆点，设类型 \(i\) 需要 \(f_i\) 道题目，那么我们把 \(i\) 拆成 \((i,1)\sim (i\sim f_i)\)，每个试题向其所有类型的所有点连边
求这个二分图上的最大匹配，判断其大小是否为 \(\sum f_i\) 即可
8. 方格取数问题
对网格黑白染色，在相邻的位置之间连边，能够得到一张二分图，答案转化为求这张二分图的最大权独立集
将最大权独立集对偶成点权和减去最小权覆盖集
对于最小权覆盖集，我们可以通过如下方式解决：
- 对于某个左部点 \(x\)，连接 \(S\to x\)，容量为 \(a_x\)
- 对于某个右部点 \(y\)，连接 \(y\to T\)，容量为 \(a_y\)
- 对于某条原本在二分图的边 \((x,y)\)，连接 \(x\to y\)，容量为 \(\infty\)
此时对于原本在二分图中的一条边 \(x\to y\)，在这里被拆成了 \(S\to x\to y\to T\)，我们求出网络上的最小割，那么此时每个 \(S\to x \to y\to T\) 的路径，\(S\to x\) 和 \(y\to T\) 至少有一个在割中，符合覆盖集的定义，因此最小权覆盖集的大小即为网络上最小割的大小
根据最小权点覆盖计算出最大权独立集的大小即可
9. 餐巾计划问题
考虑对于每个日期 \(i\) 建立两个节点分别保存当天的干净毛巾和脏毛巾，记为节点 \(i\) 和节点 \(i'\)，构图方式如下：
- 连接 \(i\to T\)，容量为 \(r_i\)，费用为 \(0\)，表示第 \(i\) 天要供应 \(r_i\) 条毛巾
- 连接 \(S\to i'\)，容量为 \(r_i\)，费用为 \(0\)，表示第 \(i\) 天结束时可以得到 \(r_i\) 条脏毛巾
- 连接 \(i'\to(i+1)'\)，容量为 \(\infty\)，费用为 \(0\)，表示第 \(i\) 天可以留下任意多条脏毛巾到下一天清洗
- 连接 \(i\to(i+1)\)，容量为 \(\infty\)，费用为 \(0\)，表示第 \(i\) 天可以留下任意多条干净毛巾到下一天使用
- 连接 \(S\to i\)，容量为 \(\infty\)，费用为 \(p\)，表示第 \(i\) 天可以 \(p\) 的单价购买任意多的干净毛巾，当天立即获得
- 连接 \(i'\to (i+m)\)，容量为 \(\infty\)，费用为 \(f\)，表示第 \(i\) 天可以以 \(f\) 的单价将任意多条毛巾送去快洗，\(i+m\) 天时获得
- 连接 \(i'\to (i+n)\)，容量为 \(\infty\)，费用为 \(s\)，表示第 \(i\) 天可以以 \(s\) 的单价将任意多条毛巾送去快洗，\(i+n\) 天时获得
我们只需要求出这个网络上的最小费用最大流，其费用即为答案
10. 软件补丁问题
对错误状态状压，把每个补丁看成一条边，求最短路即可
11. 数字梯形问题
对于问题一：
先对每个位置 \((i,j)\) 拆两个点 \((i,j),(i,j)'\)，然后按如下方式构图：
- 连接 \(S\to (1,i)\)，容量为 \(1\)，费用为 \(a_{1,i}\)，表示需要恰好一条从 \((1,i)\) 出发的路径，走到 \((1,i)\) 后获得价值 \(a_{1,i}\)
- 连接 \((i,j)\to(i,j)'\)，容量为 \(1\)，费用为 \(0\)，表示每个点至多被访问一次
- 连接 \((i,j)'\to (i+1,j)，(i,j)\to (i+1,j+1)'\) ，容量均为 \(1\)，费用分别为 \(a_{i+1,j},a_{i+1,j+1}\)，表示走到下一层的两个位置获得相应的价值
- 连接 \((n,i)'\to T\)，容量为 \(1\)，费用为 \(0\)，表示至多一条路径以 \((n,i)\) 结尾
对于问题二：
不需要拆点，按如下方式构图：
- 连接 \(S\to (1,i)\)，容量为 \(1\)，费用为 \(a_{1,i}\)，表示需要恰好一条从 \((1,i)\) 出发的路径，走到 \((1,i)\) 后获得价值 \(a_{1,i}\)
- 连接 \((i,j)'\to (i+1,j)，(i,j)\to (i+1,j+1)'\) ，容量均为 \(1\)，费用分别为 \(a_{i+1,j},a_{i+1,j+1}\)，表示每条边至多被走一次，走到下一层的两个位置获得相应的价值
- 连接 \((n,i)\to T\)，容量为 \(\infty\)，费用为 \(0\)，表示任意条路径以 \((n,i)\) 结尾
对于问题三：
不需要拆点，按如下方式构图：
- 连接 \(S\to (1,i)\)，容量为 \(1\)，费用为 \(a_{1,i}\)，表示需要恰好一条从 \((1,i)\) 出发的路径，走到 \((1,i)\) 后获得价值 \(a_{1,i}\)
- 连接 \((i,j)'\to (i+1,j)，(i,j)\to (i+1,j+1)'\) ，容量均为 \(\infty\)，费用分别为 \(a_{i+1,j},a_{i+1,j+1}\)，表示每条边可以走任意次，走到下一层的两个位置获得相应的价值
- 连接 \((n,i)\to T\)，容量为 \(\infty\)，费用为 \(0\)，表示任意条路径以 \((n,i)\) 结尾
三个问题的答案分别为这三个网络上的最大费用最大流的费用
12. 运输问题
按如下方式构图：
- 对于每个仓库 \(i\)，连接 \(S\to i\)，容量为 \(a_i\)，费用为 \(0\)，表示第 \(i\) 个仓库里有 \(a_i\) 件货物
- 对于每个商店 \(j\)，连接 \(j\to T\)，容量为 \(b_i\)，费用为 \(0\)，表示第 \(j\) 个商店需要 \(b_i\) 件货物
- 对于每个仓库 \(i\) 和商店 \(j\)，连接 \(i\to j\)，容量为 \(\infty\)，费用为 \(c_{i,j}\)，表示从第 \(i\) 个仓库到第 \(j\) 个商店可以以 \(c_{i,j}\) 的单价运输任意数量的货物
两个问题的答案即分别为这个网络上的最小费用最大流和最大费用最大流
13. 分配问题
人看成左部点，任务看成右部点，最大价值直接求二分图最大权完美匹配即可
最小价值可以选取一个足够大的值 \(A\)，把每条边的边权看成 \(A-c_{i,j}\) 满足 \(A-c_{i,j}\ge 0\) 求出最大权完美匹配的大小 \(x\)，答案即为 \(n\times A-x\)
14. 负载平衡问题
先求出 \(\{a_i\}\) 的平均值 \(\bar a\)，然后按如下方式构图
- 对于每个 \(a_i>\bar a\) 的 \(i\) 连接 \(S\to i\)，容量为 \(a_i-\bar a\)，费用为 \(0\)，表示 \(a_i\) 变成 \(\bar a\) 需要有 \(a_i-\bar a\) 件货物被运出
- 对于每个 \(a_i<\bar a\) 的 \(i\) 连接 \(i\to T\)，容量为 \(\bar a-a_i\)，费用为 \(0\)，表示 \(a_i\) 变成 \(\bar a\) 需要有 \(\bar a-a_i\) 件货物被运入
- 连接 \(i\to i+1,i\to i-1\)，容量为 \(\infty\)，费用为 \(1\)，表示可以以 \(1\) 的单价将任意多件 \(i\) 中的货品运到 \(i-1\) 或 \(i+1\) 上
答案即为这个网络上的最小费用最大流
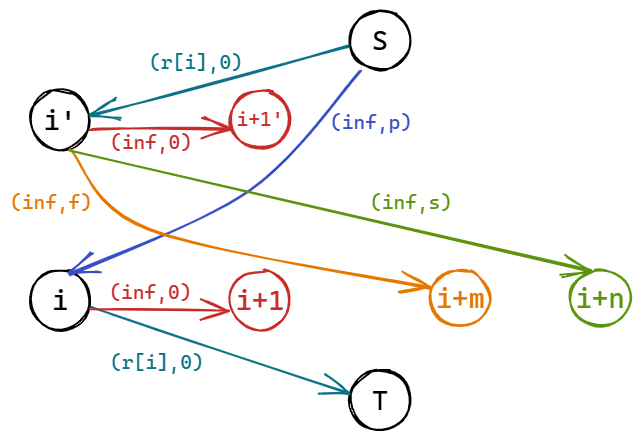
15. 最长 k 可重区间集问题
考虑对于一个 \(k\) 可重区间集，将其拆分成 \(k\) 个互不相交的区间集，可以证明这两个之间存在双射
对于一个互不相交的区间构成的集合，我们把区间从左至右排序，可以把这个区间集看成一条链
因此假如我们对于所有 \(r_j\le l_i\)，即区间 \(j\) 完全在区间 \(i\) 左侧的 \(i,j\)，连接 \(j\to i\)，并且设每个点的权值为其区间长度，那么原题可以转化为在这张图上选出至多 \(k\) 条互不相交的链并最大化链中节点的权值和
由于一个区间至多在一条链中，因此仍然需要拆点，对于每个区间 \(i\) 拆成两个点 \(i,i'\)，按如下方式构图：
- 连接 \(S\to S'\)，容量为 \(k\)，费用为 \(0\)，表示至多拆分成 \(k\) 条链
- 连接 \(S'\to i\)，容量为 \(1\)，费用为 \(0\)，表示每个点至多作为一条链的起点
- 连接 \(i'\to T\)，容量为 \(1\)，费用为 \(0\)，表示每个点至多作为一条链的终点
- 连接 \(i\to i'\)，容量为 \(1\)，费用为 \(r_i-l_i\)，表示每个区间至多被选择一次，且选择该区间的价值为 \(r_i-l_i\)
- 对于所有 \(r_i\le l_j\) 的 \(i,j\)，连接 \(i'\to j\)，容量为 \(1\)，费用为 \(0\)，表示区间 \(j\) 能与区间 \(i\) 划分在同一个链中（如果同时连接 \(i'\to j\) 和 \(j'\to i\) 可能会在残量网络上产生正环导致无法进行增广，因此要为每条边定向）
答案即为这个网络上的最大费用最大流
16. 星际转移问题
考虑增量算法，即从小到大枚举时间 \(t\)，每次修改图，如果某个时刻最大流 \(=k\) 则立刻输出 \(t\) 并退出，可以证明在有解得情况下，最长时间大约是 \(\Theta(nk)\) 级别的，因此 \(t\) 大概枚举到 \(700\) 就行，如果到 \(700\) 还找不出解则返回无解信息即可
而对于一个确定的 \(t\)，显然将图分 \(t\) 层，每层表示一个时间时的图，每次连边从第 \(t\) 层向第 \(t+1\) 层连接，并且同一个节点也要从 \(t\) 向 \(t+1\) 连接，表示人可以留在原地，具体的建图方式比较基础，简单处理一下路径连接到起点终点的情况即可
17. 孤岛营救问题
对获得钥匙的状态进行状压，并且以获得钥匙的状态进行分层，由于边权只有 \(0\) 和 \(1\)，因此在分层图上用 01BFS 求最短路即可
18. 航空路线问题
把 \(S\to T\to S\) 的路径看成两条 \(S\to T\) 的路径，然后拆点并且设置 \(S,T\) 能经过两次即可
答案即为网络上的最大费用最大流，注意特判 \(n=1\) 的情况，输出的时候 dfs 找所有被流过的边即可
19. 汽车加油行驶问题
对汽车剩余油量进行分层，在分层图上模拟建边跑最短路即可，注意加油站是强制消费的
20. 深海机器人问题
本题是比较显然的费用流，需要处理的是“每条边只有第一次经过才能获得权值”的限制，考虑拆成一条容量为 \(1\)，费用为 \(w\) 的边和一条容量为 \(\infty\)，费用为 \(0\) 的边，按如下方式构图：
- 连接 \((i,j)\to (i+1,j),(i,j)\to(i,j+1)\)，容量为 \(1\)，费用为这条路径上生物标本的价值，表示第一个走这条路径的机器人能够获得相应的价值
- 连接 \((i,j)\to(i+1,j),(i,j)\to(i,j+1)\)，容量为 \(\infty\)，费用为 \(0\)，表示后面走这条路径的机器人无法获得价值，但依然可以通过这条路径
- 对于每个起点 \((k,x,y)\) 连接 \(S\to (x,y)\)，容量为 \(k\)，费用为 \(0\)，表示从 \((x,y)\) 出发的有 \(k\) 个机器人
- 对于每个起点 \((r,x,y)\) 连接 \((x,y)\to T\)，容量为 \(r\)，费用为 \(0\)，表示在 \((x,y)\) 结束的有 \(r\) 个机器人
答案即为这个网络上的最大费用最大流
21. 火星探险问题
类似上一题，不过这一次需要先拆点再对点分流贡献，按如下方式构图：
- 连接 \(S\to (1,1)\)，容量为 \(car\)，费用为 \(0\)，表示 \(car\) 辆探险车从 \((1,1)\) 出发
- 连接 \((p,q)'\to T\) ，容量为 \(car\)，费用为 \(0\)，表示至多 \(car\) 辆探险车到达 \((p,q)\) 处才能被统计贡献
- 对于 \(a_{i,j}=0\)，连接 \((i,j)\to (i,j)'\)，容量为 $\infty $，费用为 \(0\)，表示可以经过空地任意次
- 对于 \(a_{i,j}=1\)，断开 \((i,j),(i,j)'\)，表示到达这里之后不能继续前进
- 对于 \(a_{i,j}=2\)，连接 \((i,j)\to (i,j)'\)，容量为 \(1\)，费用为 \(1\)，表示第一个经过这里的机器人可以获得 \(1\) 块样本，再连接 \((i,j)\to (i,j)'\)，容量为 \(\infty\)，费用为 \(0\)，表示之后到这里的机器人可以经过这里任意次
- 连接所有 \((i,j)'\to (i+1,j),(i,j)'\to (i,j+1)\)，容量为 \(\infty\)，费用为 \(0\)，表示机器人向南走或者向东走
答案即为网络上的最大费用最大流，输出答案的时候进行 \(car\) 次 dfs，每次找到一条路径然后将反向边流量 \(-1\)，转移的时候根据反向边流量是否 \(>0\) 来判断是否还有路径经过这条边
22. 骑士共存问题
将所有互相攻击的点对连起来，发现对网格图黑白染色之后会形成二分图，因此答案即为二分图上最大独立集大小
用所有未被删除的点的数量减去二分图的最大匹配的大小即得到答案，注意本题数据范围朴素的增广路算法无法通过，请使用 HK 算法或最大流解决此题
23. 最长 k 可重线段集
和第 15 题基本一致，注意可重线段可能出现两条 \(x_0=x_1\) 的竖直线段重合的情况，需要进行一点特判
