01-线性回归算法
机器学习分类:回归,分类
回归:最终得到的是在一个区间上真正(实际)的值
分类:最终得到的是个逻辑值0/1,是与不是,能与不能之类的答案
名词解释:
拟合:拟合就是把平面上一系列的点,用一条光滑的曲线连接起来。因为这条曲线有无数种可能,从而有各种拟合方法。拟合的曲线一般可以用函数表示,根据这个函数的不同有不同的拟合名字。
最小二乘法:最小二乘法(又称最小平方法)是一种数学优化技术。它通过最小化误差的平方和寻找数据的最佳函数匹配。利用最小二乘法可以简便地求得未知的数据,并使得这些求得的数据与实际数据之间误差的平方和为最小。最小二乘法还可用于曲线拟合。其他一些优化问题也可通过最小化能量或最大化熵用最小二乘法来表达
回归问题举例:


对问题进行数学化:
X1,X2就是我们的两个特征值(年龄,工资),而Y是最终银行会借给我们多少钱。
需要解决的问题就是:找到一条来最好拟合我们数据的点。
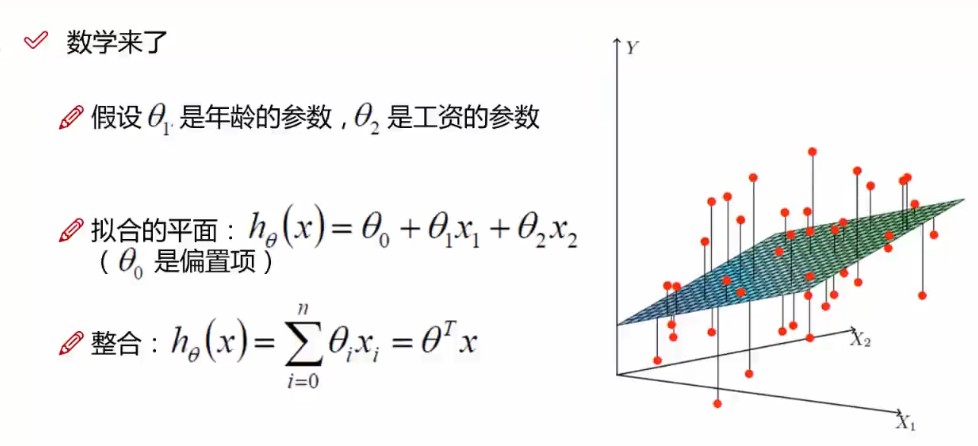
最终得到的整合的h(x)主要是为了使数据看起来更加的整齐,也方便以后的矩阵运算。
误差分析:

误差三个特性:独立,同分布,高斯分布


似然函数求解:

eg: 简化运算:log(AB) = logA + logB

目标函数求解:求J(0)的最小值 注意:样本服从高斯分布且独立,其最大似然估计就可以用最小二乘形式表示。
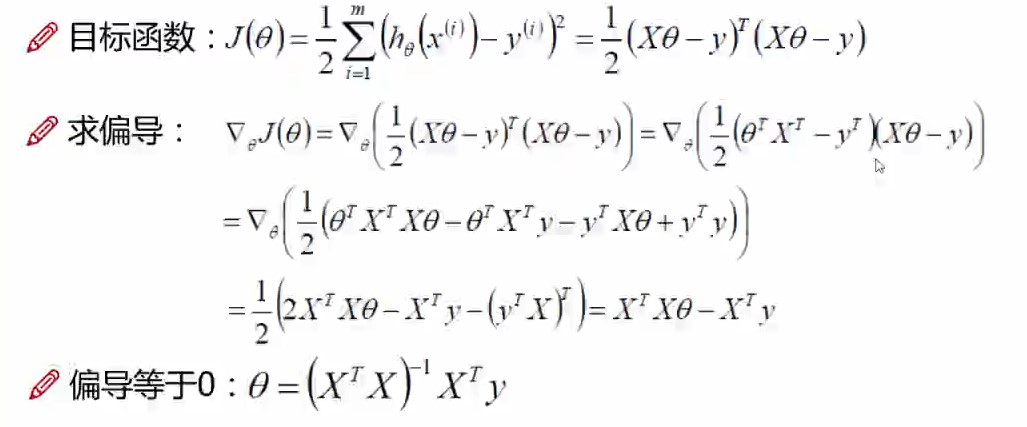
X,Y为已知的数据,即可求得佘塔
评估方法:
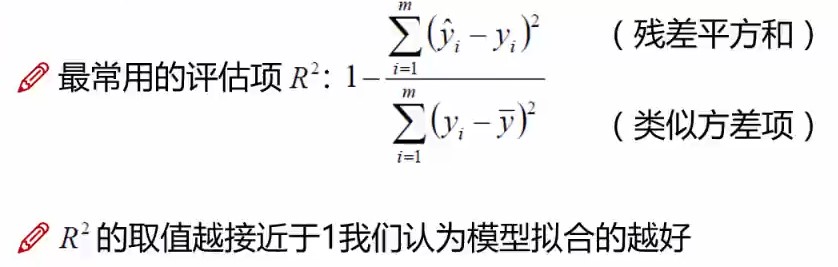
<wiz_tmp_tag id="wiz-table-range-border" contenteditable="false" style="display: none;">


