【Codeforces715C&716E】Digit Tree 数学 + 点分治

C. Digit Tree

time limit per test：3 seconds
memory limit per test：256 megabytes
input：standard input
output：standard output

ZS the Coder has a large tree. It can be represented as an undirected connected graph of n vertices numbered from 0 to n - 1 and n - 1edges between them. There is a single nonzero digit written on each edge.

One day, ZS the Coder was bored and decided to investigate some properties of the tree. He chose a positive integer M, which iscoprime to 10, i.e. .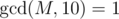

ZS consider an ordered pair of distinct vertices (u, v) interesting when if he would follow the shortest path from vertex u to vertex v and write down all the digits he encounters on his path in the same order, he will get a decimal representaion of an integer divisible by M.

Formally, ZS consider an ordered pair of distinct vertices (u, v) interesting if the following states true:

  • Let a1 = u, a2, ..., ak = v be the sequence of vertices on the shortest path from u to v in the order of encountering them;
  • Let di (1 ≤ i < k) be the digit written on the edge between vertices ai and ai + 1;
  • The integer 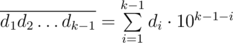 is divisible by M.

Help ZS the Coder find the number of interesting pairs!

Input

The first line of the input contains two integers, n and M (2 ≤ n ≤ 100 000, 1 ≤ M ≤ 109, 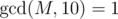) — the number of vertices and the number ZS has chosen respectively.

The next n - 1 lines contain three integers each. i-th of them contains ui, vi and wi, denoting an edge between vertices ui and vi with digit wi written on it (0 ≤ ui, vi < n,  1 ≤ wi ≤ 9).

Output

Print a single integer — the number of interesting (by ZS the Coder's consideration) pairs.

Examples

input
6 7
0 1 2
4 2 4
2 0 1
3 0 9
2 5 7
output
7
input
5 11
1 2 3
2 0 3
3 0 3
4 3 3
output
8

Note

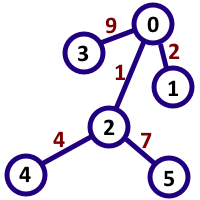
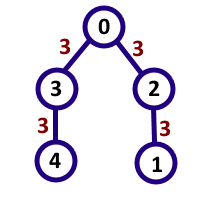
In the first sample case, the interesting pairs are (0, 4), (1, 2), (1, 5), (3, 2), (2, 5), (5, 2), (3, 5). The numbers that are formed by these pairs are 14, 21, 217, 91, 7, 7, 917 respectively, which are all multiples of 7. Note that (2, 5) and (5, 2) are considered different.

In the second sample case, the interesting pairs are (4, 0), (0, 4), (3, 2), (2, 3), (0, 1), (1, 0), (4, 1), (1, 4), and 6 of these pairs give the number 33 while 2 of them give the number 3333, which are all multiples of 11.

Solution

一道比较好想好写的点分治

点分治显然，考虑如何计算复合的路径条数。

对于每个点我们维护两个值$Dig[x],Dig'[x]$，表示重心到这个点的路径组成的数,以及这个点到重心组成的数

这样对于一个点对$<u,v>$我们可以知道他们的$Dig[u],Dig[v],Dig'[u],Dig'[v]$，那么他们所组成的数就是$Dig'[u]*10^{k}+Dig[v]$

这个$k$我们发现，就相当于是$deep[u]$，知道这些就有思路搞了

题目的要求就是$Dig<u,v>mod M=0$也就可以转化成$Dig'[u]*10^{deep[u]}+Dig[v]\equiv 0(modM)$

然后整理一下就可以得到$Dig'[u]\equiv -Dig[v]*\frac{1}{10^{deep[u]}}$

然后用map存一下式子右边，对于一个点，它对答案的贡献就是hash表里的$Dig'[u]$的数量

Code

#include<iostream>
#include<cstdio>
#include<cstring>
#include<cmath>
#include<algorithm>
#include<map>
using namespace std;
#define LL long long
inline int read()
{
    int x=0,f=1; char ch=getchar();
    while (ch<'0' || ch>'9') {if (ch=='-') f=-1; ch=getchar();}
    while (ch>='0' && ch<='9') {x=x*10+ch-'0'; ch=getchar();}
    return x*f;
}
#define MAXN 100010
int N,M;
map<LL,LL>hash;
LL ans;
namespace Math
{
    LL power[MAXN],Inv[MAXN];
    inline LL Gcd(LL a,LL b) {if (!b) return a; else return Gcd(b,a%b);}
    inline void ExGcd(LL a,LL b,LL &x,LL &y) {if (!b) {x=1,y=0; return;} ExGcd(b,a%b,y,x); y-=(a/b)*x;}
    inline LL inv(LL X) {LL x,y; ExGcd(X,M,x,y); return (x%M+M)%M;}
    inline LL Pow(LL x,LL y) {LL re=1; for (LL i=y; i; i>>=1,x=x*x%M) if (i&1) re=re*x%M; return re;}
}
using namespace Math;
namespace TreeDivide
{
    struct EdgeNode{int next,to,val;}edge[MAXN<<1];
    int head[MAXN],cnt=1; 
    inline void AddEdge(int u,int v,int w) {cnt++; edge[cnt].to=v; edge[cnt].next=head[u]; head[u]=cnt; edge[cnt].val=w;}
    inline void InsertEdge(int u,int v,int w) {AddEdge(u,v,w); AddEdge(v,u,w);}
    int size[MAXN],f[MAXN],visit[MAXN],root,deep[MAXN],Sz;
    LL Dig[MAXN];
    inline void Getroot(int x,int last)
    {
        size[x]=1,f[x]=0;
        for (int i=head[x]; i; i=edge[i].next)
            if (!visit[edge[i].to] && edge[i].to!=last)
                {
                    Getroot(edge[i].to,x);
                    size[x]+=size[edge[i].to];
                    f[x]=max(f[x],size[edge[i].to]);
                }
        f[x]=max(f[x],Sz-f[x]);
        if (f[x]<f[root]) root=x;
    }
    inline void DFS(int now,int last)
    {
        LL D=(((M-Dig[now])+M)%M*Inv[deep[now]])%M; hash[D]++;
        for (int i=head[now]; i; i=edge[i].next)
            if (edge[i].to!=last && !visit[edge[i].to])
                deep[edge[i].to]=deep[now]+1,
                Dig[edge[i].to]=(Dig[now]*10%M+edge[i].val)%M,
                DFS(edge[i].to,now);
    }
    inline LL Get(int now,int last)
    {
        LL re=hash[Dig[now]];
        for (int i=head[now]; i; i=edge[i].next)
            if (edge[i].to!=last && !visit[edge[i].to])
                Dig[edge[i].to]=(edge[i].val*power[deep[now]]%M+Dig[now])%M,
                deep[edge[i].to]=deep[now]+1,
                re+=Get(edge[i].to,now);
        return re;
    }
    inline void Divide(int now)
    {
        visit[now]=1;
        hash.clear(); hash[0]--;
        Dig[now]=0LL,deep[now]=0;
        DFS(now,0);
        ans+=Get(now,0);
        for (int i=head[now]; i; i=edge[i].next)
            if (!visit[edge[i].to])
                hash.clear(),hash[0]--,
                Dig[edge[i].to]=edge[i].val%M,deep[edge[i].to]=1,
                DFS(edge[i].to,now),
                ans-=Get(edge[i].to,now);
        for (int i=head[now]; i; i=edge[i].next)
            if (!visit[edge[i].to])
                Sz=size[edge[i].to],f[root=0]=N,
                Getroot(edge[i].to,now),Divide(root);
    }
}
using namespace TreeDivide;
int main()
{
    N=read(),M=read();
    for (int x,y,z,i=1; i<=N-1; i++) x=read()+1,y=read()+1,z=read(),InsertEdge(x,y,z);
    for (int i=0; i<=N; i++) power[i]=Pow(10,i),Inv[i]=inv(power[i]);
    Sz=N; f[root=0]=N+1; 
    Getroot(1,0); Divide(root);
    printf("%I64d\n",ans);
    return 0;
}

 

posted @ 2016-09-30 18:34  DaD3zZ  阅读(495)  评论(0)  编辑  收藏  举报