【Codefoces487E/UOJ#30】Tourists Tarjan 点双连通分量 + 树链剖分

E. Tourists

time limit per test:
2 seconds
memory limit per test:
256 megabytes
input:
standard input
output
:standard output

There are n cities in Cyberland, numbered from 1 to n, connected by m bidirectional roads. The j-th road connects city aj and bj.

For tourists, souvenirs are sold in every city of Cyberland. In particular, city i sell it at a price of wi.

Now there are q queries for you to handle. There are two types of queries:

  • "C a w": The price in city a is changed to w.
  • "A a b": Now a tourist will travel from city a to b. He will choose a route, he also doesn't want to visit a city twice. He will buy souvenirs at the city where the souvenirs are the cheapest (possibly exactly at city a or b). You should output the minimum possible price that he can buy the souvenirs during his travel.

More formally, we can define routes as follow:

  • A route is a sequence of cities [x1, x2, ..., xk], where k is a certain positive integer.
  • For any 1 ≤ i < j ≤ k, xi ≠ xj.
  • For any 1 ≤ i < k, there is a road connecting xi and xi + 1.
  • The minimum price of the route is min(wx1, wx2, ..., wxk).
  • The required answer is the minimum value of the minimum prices of all valid routes from a to b.

Input

The first line of input contains three integers n, m, q (1 ≤ n, m, q ≤ 105), separated by a single space.

Next n lines contain integers wi (1 ≤ wi ≤ 109).

Next m lines contain pairs of space-separated integers aj and bj (1 ≤ aj, bj ≤ n, aj ≠ bj).

It is guaranteed that there is at most one road connecting the same pair of cities. There is always at least one valid route between any two cities.

Next q lines each describe a query. The format is "C a w" or "A a b" (1 ≤ a, b ≤ n, 1 ≤ w ≤ 109).

Output

For each query of type "A", output the corresponding answer.

Examples

input
3 3 3
1
2
3
1 2
2 3
1 3
A 2 3
C 1 5
A 2 3
output
1
2
input
7 9 4
1
2
3
4
5
6
7
1 2
2 5
1 5
2 3
3 4
2 4
5 6
6 7
5 7
A 2 3
A 6 4
A 6 7
A 3 3

output

2
1
5
3

Note

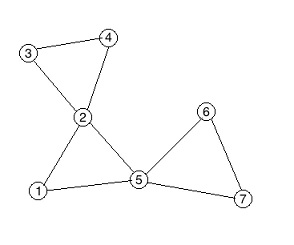
For the second sample, an optimal routes are:

From 2 to 3 it is [2, 3].

From 6 to 4 it is [6, 5, 1, 2, 4].

From 6 to 7 it is [6, 5, 7].

From 3 to 3 it is [3].

Solution

中文题面见UOJ#30  ： UOJ#30

思路比较显然，把图缩点重建，再利用数据结构去维护。

要求简单路径，显然可以考虑点双连通分量，我们先对图Tarjan求点双连通分量，然后将这些BCC维护一个最小值，然后缩成一个点，这样就形成一棵树，就可以树剖。

但是这里有一个问题，割点可能会存在于多个点双连通分量中，而这会比较蛋疼，因为割点的答案显然应该是距离它最小的那个。

所以我们对割点单独处理，每个割点新建一个点单独向它所在的所有点双连通分量连一条边； 这样我们就可以在询问的时候，搞定割点的问题了。

那么修改一个点，这个点所在点双的值就有可能发生改变，如果修改割点，那么就会对很多点双造成影响，所以要特殊处理这种情况。

但是我们发现，我们这样建出来的新图（树）一定是满足 块->割点->块->割点 的。

所以我们不妨定义一个点双维护的是，这个点双中除了它fa的割点的所有点的权值+连向它的割点的权值最小，这样如果修改一个割点，就只会影响到它的fa点双。

查询的时候，我们查询$<u,v>$，如果$LCA(u,v)$是一个割点，我们可以直接统计答案。 如果$LCA(u,v)$是一个点双，那么我们还得查它的fa割点的值。

点双内的最小值，可以用multiset来维护。

这样的查询复杂度是$O(log^{2}N)$，修改的复杂度是$O(logN)$，总的复杂度就是$O(Nlog^{2}N)$

对于Tarjan点双连通分量，网上有些人说要边入栈，但很多人却写的点入栈，其实都是可以的。 但是这道题，如果用边入栈的方法，在连边的时候会连出问题的，需要额外判，所以就用来点入栈的方法。

Code

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cmath>
#include<vector>
#include<set>
#include<cstring>
using namespace std;
inline int read()
{
    int x=0; char ch=getchar();
    while (ch<'0' || ch>'9') {ch=getchar();}
    while (ch>='0' && ch<='9') {x=x*10+ch-'0'; ch=getchar();}
    return x;
}
#define INF 0x7fffffff
#define MAXN 100100
int N,M,Q,val[MAXN],Val[MAXN<<1];
struct RoadNode{int next,to;}road[MAXN<<1];
int tot=1,first[MAXN];
struct EdgeNode{int next,to;}edge[MAXN<<2];
int cnt=1,head[MAXN<<1];
inline void AddEdge(int u,int v) {cnt++; edge[cnt].next=head[u]; head[u]=cnt; edge[cnt].to=v;}
inline void InsertEdge(int u,int v) {AddEdge(u,v); AddEdge(v,u);}
multiset<int>::iterator ist;
struct BlockNode
{
    multiset<int>st; int val; 
    inline void insert(int x) {st.insert(x); val=*st.begin();}
    inline void change(int x,int y) {st.erase(*st.find(x)); st.insert(y); val=*st.begin();}
}B[MAXN<<1];
namespace Graph
{
    inline void AddRoad(int u,int v) {tot++; road[tot].next=first[u]; first[u]=tot; road[tot].to=v;}
    inline void InsertRoad(int u,int v) {AddRoad(u,v); AddRoad(v,u);}
    int dfn[MAXN],low[MAXN],dfsn,bcc,now,belong[MAXN],size[MAXN],cut[MAXN],st[MAXN],top;
    inline void Tarjan(int now)
    {
        dfn[now]=low[now]=++dfsn; st[++top]=now;
        for (int i=first[now]; i; i=road[i].next)    
            if (!dfn[road[i].to])
                {
                    Tarjan(road[i].to); low[now]=min(low[now],low[road[i].to]);
                    if (dfn[now]<=low[road[i].to])
                        {
                            bcc++; cut[now]=1; int tp=0;
                            while (1) 
                                {
                                    tp=st[top--]; belong[tp]=bcc; 
                                    if (cut[tp]) InsertEdge(tp+N,bcc); if (tp==road[i].to) break;
                                }
                            InsertEdge(now+N,bcc);
                        }
                }
            else low[now]=min(low[now],dfn[road[i].to]);
    }
    inline void reBuild()
    {
        for (int i=1; i<=N; i++) if (!dfn[i]) Tarjan(i);
        for (int i=1; i<=N; i++)
            {
                if (i!=1) B[belong[i]].insert(val[i]);
                if (cut[i]) B[i+N].insert(INF);
            }
    }
}
namespace SegmentTree
{
    struct SegmentTreeNode{int l,r,minx;}tree[MAXN<<3];
    #define ls now<<1
    #define rs now<<1|1
    inline void Update(int now) {tree[now].minx=min(tree[ls].minx,tree[rs].minx);}
    inline void BuildTree(int now,int l,int r)
    {
        tree[now].l=l; tree[now].r=r;
        if (l==r) {tree[now].minx=Val[l]; return;}
        int mid=(l+r)>>1;
        BuildTree(ls,l,mid); BuildTree(rs,mid+1,r);
        Update(now);
    }
    inline void Change(int now,int pos,int D) 
    {
        int l=tree[now].l,r=tree[now].r;
        if (l==r) {tree[now].minx=D; return;}
        int mid=(l+r)>>1;
        if (pos<=mid) Change(ls,pos,D);
        if (pos>mid) Change(rs,pos,D);
        Update(now);
    }
    inline int Query(int now,int L,int R)
    {
        int l=tree[now].l,r=tree[now].r;
        if (L<=l && R>=r) return tree[now].minx;
        int mid=(l+r)>>1,re=INF;
        if (L<=mid) re=min(re,Query(ls,L,R));
        if (R>mid) re=min(re,Query(rs,L,R));
        return re;
    }
}
namespace TreePartition
{
    int fa[MAXN<<1],size[MAXN<<1],son[MAXN<<1],deep[MAXN<<1],pl[MAXN<<1],dfn,pre[MAXN<<1],top[MAXN<<1];
    inline void DFS_1(int now)
    {
        size[now]=1;
        for (int i=head[now]; i; i=edge[i].next)
            if (edge[i].to!=fa[now])
                {
                    fa[edge[i].to]=now;
                    deep[edge[i].to]=deep[now]+1;
                    DFS_1(edge[i].to);
                    size[now]+=size[edge[i].to];
                    if (size[son[now]]<size[edge[i].to]) son[now]=edge[i].to;    
                }
    }
    inline void DFS_2(int now,int chain)
    {
        pl[now]=++dfn; pre[dfn]=now;  top[now]=chain; Val[dfn]=B[now].val;
        if (son[now]) DFS_2(son[now],chain);
        for (int i=head[now]; i; i=edge[i].next)
            if (edge[i].to!=fa[now] && edge[i].to!=son[now])
                DFS_2(edge[i].to,edge[i].to);
    }
    inline int LCA(int u,int v)
    {
        while (top[u]!=top[v])
                {
                if (deep[top[u]]<deep[top[v]]) swap(u,v);
                u=fa[top[u]];
            }
        if (deep[u]>deep[v]) swap(u,v);
        return u;
    }
    inline int Query(int x,int y)
    {
        x=Graph::cut[x]? x+N:Graph::belong[x]; y=Graph::cut[y]? y+N:Graph::belong[y];
        int re=INF; int lca=LCA(x,y);
        if (lca<=Graph::bcc) lca=fa[lca]; re=val[lca-N];
        while (top[x]!=top[y])
            {
                if (deep[top[x]]<deep[top[y]]) swap(x,y);
                re=min(re,SegmentTree::Query(1,pl[top[x]],pl[x]));
                x=fa[top[x]];
            }
        if (deep[x]>deep[y]) swap(x,y);
        re=min(re,SegmentTree::Query(1,pl[x],pl[y]));
        return re;
    }
    inline void Change(int pos,int D) {SegmentTree::Change(1,pl[pos],D);}
}
int main()
{
    N=read(),M=read(),Q=read();
    for (int i=1; i<=N; i++) val[i]=read();
    for (int x,y,i=1; i<=M; i++) x=read(),y=read(),Graph::InsertRoad(x,y);
    Graph::reBuild();
//    for (int i=1; i<=N; i++) printf("%d %d %d %d\n",dfn[i],low[i],cut[i],belong[i]);
    TreePartition::DFS_1(N+1); TreePartition::DFS_2(N+1,N+1);
    SegmentTree::BuildTree(1,1,TreePartition::dfn);
    while (Q--)
        {
            char opt[2]; scanf("%s",opt); int x=read(),y=read();
            switch (opt[0])
                {
                    case 'C': if (x!=1) {B[Graph::belong[x]].change(val[x],y); TreePartition::Change(Graph::belong[x],B[Graph::belong[x]].val);} val[x]=y; break;
                    case 'A': if (x==y) printf("%d\n",val[x]); else printf("%d\n",TreePartition::Query(x,y)); break;
                }
        }
    return 0;
}

UOJ上跑的还挺快QAQ...就是死活压不到6000ms+....

posted @ 2016-09-25 19:12  DaD3zZ  阅读(671)  评论(0)  编辑  收藏  举报