【2023.11.16】NOIP2023模拟试题-35
《信心赛》
《很简单》
T1
\(O(n\log n)\) 居然卡不过去（愤怒）
所以我们需要研发 \(O(n)\) 的算法：单调队列。
维护两个指针 \(l,r\) 从最左边开始扫，只要极差小于 \(k\) 就把 \(r\) 一直往右边挪，只要极差大于 \(k\) 就把 \(l\) 往右边挪，这样能确保永远是能取最大的一段区间 。
查看代码
#include<bits/stdc++.h>
using namespace std;
#define fi(l,r) for(int i=l;i<=r;++i)
#define ff(i,l,r) for(int i=l;i<=r;++i)
#define ll long long
#define ly __int128
#define lp ll
#define lson(x) ((x)<<1)
#define rson(x) (lson(x)|1)
#define Lson(x) tr[lson(x)]
#define Rson(x) tr[rson(x)]
#define mod %P
#define N 3000005
int len,n,d,p[N][2],h[2],t[2],l,r,ans;
ll a[N],q[N][2],mx[N],mn[N];
char buf[100000000],*it=buf;//0最小 1最大
void movr(){
++r;
while(h[0]<=t[0]&&q[t[0]][0]>=a[r])--t[0];
q[++t[0]][0]=a[r];
p[t[0]][0]=r;
while(h[1]<=t[1]&&q[t[1]][1]<=a[r])--t[1];
q[++t[1]][1]=a[r];
p[t[1]][1]=r;
}
void movl(){
++l;
while(p[h[0]][0]<l)++h[0];
while(p[h[1]][1]<l)++h[1];
return;
}
void reread(){
fread(buf,1,sizeof buf,stdin);
it=buf;
return;
}
template<typename T>
void read(T &x){
x=0;
while(!isdigit(*it))if(*(++it)==EOF)reread();
while(isdigit(*it)){
x=x*10+(*it)-'0';
if(*(++it)==EOF)reread();
}
return;
}
int main(){
freopen("sequence.in","r",stdin);
freopen("sequence.out","w",stdout);
fread(buf,1,sizeof buf,stdin);
read(d);read(n);
fi(1,n)read(a[i]);
l=h[0]=h[1]=1,r=t[0]=t[1]=0;
while(r<=n){
while(l<r&&q[h[1]][1]-q[h[0]][0]>d)movl();
while(r<=n&&q[h[1]][1]-q[h[0]][0]<=d)movr();
ans=max(ans,r-l);
movr();
}
printf("%d\n",ans);
return 0;
}
T2
题目描述：
打个表：
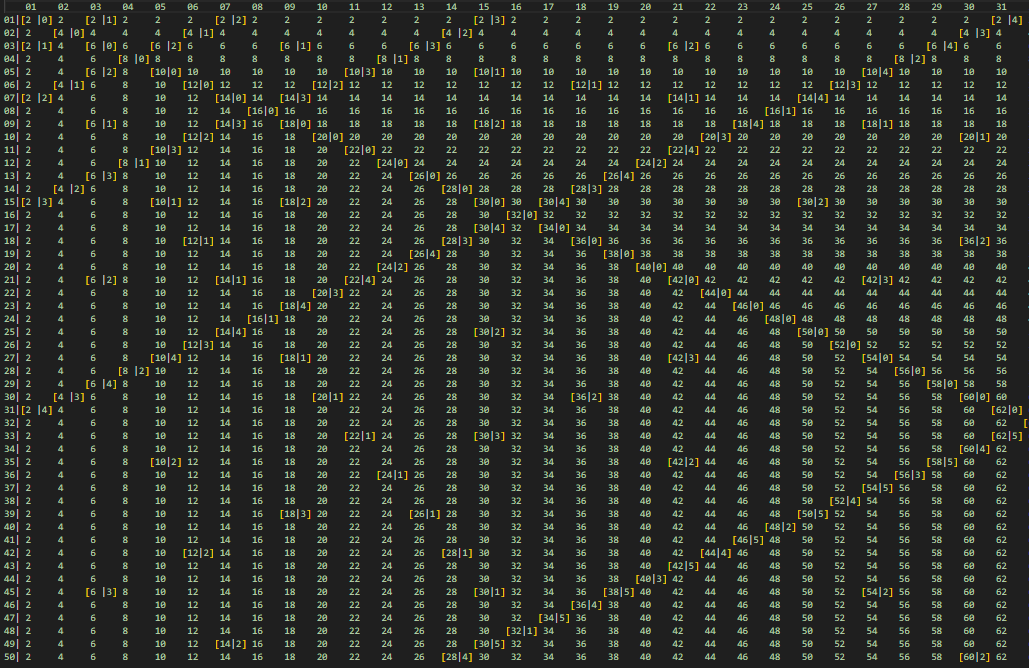
用小金方括号框起来的是值不为 \(0\) 的数，总结规律发现用以下代码
#define ctz __builtin_ctz
fi(1,n)
if((i&1)==0)
for(int bas=i>>ctz(i),j=max(bas,(i*2-n+bas-1)/bas*bas);j<=n&&j<i*2;j+=bas)
printf("x=%d y=%d val=%d\n",j,i*2-j,ctz(i)+1-ctz(j));
可以筛出所有值不为 \(0\) 的数的值。一共 \(97\) 万个，因此我们要寻找一个 \(n\log n\) 的做法。
首先我们考虑 \(a_i=i\) 的情况怎么做，其实就是问一个倒三角形区间里包含的所有 \(f\) 的和，比如询问 \(l=8,r=18\) 就是求这个区间内金色中括号数值的和：
看到三角形面积覆盖驱使我们想到扫描线或者树状数组，这里选择用树状数组来写，因为更简单。
把一个一个金色小括号看成是点，我们按照每个点的 \(x\) 坐标排序，依次按照 \(x : 1 \rightarrow n\) 的顺序加入点，每加入一列的点，就处理所有以 \(x\) 为右端点的询问：
我们把加入的点放进树状数组里，每次只需要 \(O(\log n)\) 查询 \(y\) 坐标 \(\ge l\) 的就行了。
再考虑 \(a_i\) 是排列的情况，只需要把坐标轴按照 \(a_i\) 的顺序逆变换就行了：
#define ctz __builtin_ctz
fi(1,n){
read(a[i]);
rev[a[i]]=i;
}
fi(1,n)
if((i&1)==0)
for(int bas=i>>ctz(i),j=max(bas,(i*2-n+bas-1)/bas*bas);j<=n&&j<i*2;j+=bas)
if(rev[j]>rev[i*2-j])
fri[rev[j]].push_back((Pi){rev[i*2-j],ctz(i)+1-ctz(j)});//筛出所有 f
拼合起来就得到了最终代码：
查看代码
#include<bits/stdc++.h>
using namespace std;
#define fi(l,r) for(int i=l;i<=r;++i)
#define ff(i,l,r) for(int i=l;i<=r;++i)
#define ll long long
#define ly __int128
#define lp ll
#define lson(x) ((x)<<1)
#define rson(x) (lson(x)|1)
#define Lson(x) tr[lson(x)]
#define Rson(x) tr[rson(x)]
#define mod %P
#define N 300005
#define M 1000005
#define ctz __builtin_ctz
char buf[100000005],*it;
void reread(){
fread(buf,1,sizeof buf,stdin);
it=buf;
return;
}
template<typename T>
void read(T &x){
x=0;
while(!isdigit(*it))if(*(++it)==EOF)reread();
while(isdigit(*it)){
x=x*10+(*it)-'0';
if(*(++it)==EOF)reread();
}
return;
}
int lowbit(int x){return x&(-x);}
int n,m,l,r,a[N],rev[N],c[N];
ll ans,ansof[M];
struct Pi{
int x,y;
bool operator < (Pi b){
return x<b.x;
}
};
vector<Pi>fri[N],queat[N];
bool book[N]={0};
void add(int x,int val){//存储 fri[i].x > que[i].x 的个数
while(x<=n){
c[x]+=val;
x+=lowbit(x);
}
}
int query(int r){
int ret=0;
while(r>0){
ret+=c[r];
r-=lowbit(r);
}
return ret;
}
int query(int l,int r){//查询 fri[i].x > l
return query(r)-query(l-1);
}
int main(){
freopen("perm.in","r",stdin);
freopen("perm.out","w",stdout);
reread();
int x,y;
read(n);
fi(1,n){
read(a[i]);
rev[a[i]]=i;
}
fi(1,n)
if((i&1)==0)
for(int bas=i>>ctz(i),j=max(bas,(i*2-n+bas-1)/bas*bas);j<=n&&j<i*2;j+=bas)
if(rev[j]>rev[i*2-j])
fri[rev[j]].push_back((Pi){rev[i*2-j],ctz(i)+1-ctz(j)});
read(m);
fi(1,m){
read(x);read(y);
queat[y].push_back((Pi){x,i});
}
fi(1,n){
for(Pi e:fri[i])add(e.x,e.y);
for(Pi e:queat[i])ansof[e.y]=query(e.x,i);
}
fi(1,m)printf("%lld\n",ansof[i]);
return 0;
}
T3
好不容易因为数据水做对了一遍 T3
T3 是用 dfs 乱搞出来的。先枚举第一个点 \(p_1\) ，再用 dfs 算出后面的点。理论上复杂度可以卡到 \(n^3\) ，但是没想到就这样放我 AC 了（？
查看代码
#include<bits/stdc++.h>
using namespace std;
#define fi(l,r) for(int i=l;i<=r;++i)
#define ff(i,l,r) for(int i=l;i<=r;++i)
#define ll long long
#define N 1000005
#define M 2000005
int n,m,tot,fir[N],nxt[M],to[M],kk,dis[N],ans=0x3f3f3f2f,w[M],rge[N];//dis 存储 1 到 x 只经过一条边的最短距离，rge 存储 x 到 n 只经过一条边的最短距离。
void add(int x,int y,int z){
nxt[++tot]=fir[x];
fir[x]=tot;
to[tot]=y;
w[tot]=z;
}
bool vis[N]={0};
void dfs(int x,int len,int dep){
if(len>ans)return;
if(dep==kk-1){
ans=min(ans,rge[x]+len);
return;
}
for(int e=fir[x];e;e=nxt[e]){
int u=to[e];
if(vis[u])continue;
vis[u]=1;
dfs(u,len+w[e],dep+1);
vis[u]=0;
}
return;
}
int main(){
freopen("graph.in","r",stdin);
freopen("graph.out","w",stdout);
int x,y,z;
memset(dis,0x3f,sizeof dis);
memset(rge,0x3f,sizeof rge);
scanf("%d %d %d",&n,&m,&kk);
if(kk==0){
printf("0");
return 0;
}
fi(1,m){
scanf("%d %d %d",&x,&y,&z);
add(x,y,z);
add(y,x,z);
if(x==1)dis[y]=min(dis[y],z);
if(y==1)dis[x]=min(dis[x],z);
if(x==n)rge[y]=min(rge[y],z);
if(y==n)rge[x]=min(rge[x],z);
}
if(kk==1){
if(dis[n]>=0x3f3f3f2f)printf("-1");
else printf("%d",dis[n]);
return 0;
}
if(kk==2){
fi(1,n)ans=min(ans,dis[i]+rge[i]);
if(ans>=0x3f3f3f2f)printf("-1");
else printf("%d",ans);
return 0;
}
vis[1]=vis[n]=1;
fi(2,n-1){
if(dis[i]<ans){
vis[i]=1;
dfs(i,dis[i],1);
vis[i]=0;
}
}
if(ans>=0x3f3f3f2f)printf("-1");
else printf("%d",ans);
return 0;
}
而且还比 std 快 （ ！
