【2023.11.14】NOIP2023模拟试题-34
T1
个人认为 T1 比 T2 难。
首先我们可以把答案转化成 \(A\) 是 \(P\) 的子序列串的数量 减去 \(f_K(P)=A\) 的串数量。
\(A\) 是 \(P\) 的子序列串的数量显然是 \(C_n^k\times(n-k)\;!=\frac{n!}{k!}\) .
而考虑 \(f_K(P)=A\) 的串的数量，先考虑当 \(P\) 是升序序列的情况。
对于串 \(P=\) 2 3 5 7 8 ，考虑按顺序插入 \(1\) , \(4\) , \(6\) , \(9\) , \(10\) 得到长度为 \(10\) 的排列 \(A\) 。
显然 \(1\) 只能插在 \(2\) 之前得到 1 2 3 5 7 8 。
\(4\) 可以插在 \(1\) 之前，也可以插在 \(1,2、2,3\) 之间。由于 \(3\) 是最后一个 \(<4\) 的数，\(3\) 之后就不能放 \(4\) 了，否则 \(P\) 串就可以被字典序更小的 4 顶替掉一个位置。
\(6\) 可以插在 \(1\) 之前，也可以插在 \(2,3,4\) 之前一共 \(4\) 个空位里。
\(9\) 比 \(P\) 排列的所有数都更大，可以插进 \(1,2,3,4,5,6,7,8\) 之前的 \(8\) 个空位里，也可以插进序列末尾，一共 \(9\) 个选择。
\(10\) 由于多了一个 \(9\) 之前的空位，一共有 \(10\) 个可以插的地方。
因此，满足 \(f_K(P)=A\) 的长度为 \(10\) 的序列一共有 \(1\times 3 \times 4 \times 9 \times 10 = 1080\) 个。因此答案是 \(29160\) .
我们总结规律得出，设缺失的数为 \(i\)，假设 \(i\) 以前的数都填了，填了 \(aprd\) 个，那么
由于 upper_bound 查询的结果一定随着 \(l\) 的单调递增而单调递增，所以我们可以用双指针优化，用 \(las\) 存储当前指针。
#define fi(l,r) for(int i=l;i<=r;++i)
fi(1,n){
if(apr[i]==0){
while(las<kk&&a[las+1]<i)++las;
sub=sub*(las+aprd)%P;
++aprd;
}
}
至于如果序列不是升序，我们只用去前面最长的连续一节升序序列就行了，后面的序列没卵用。为什么？因为无论插什么数都不能插在后面数之后的空位里，比如这个例子：
2 3 8 5 7
8 后面 \(1,4,6,9,10\) 都不能插，不然就给了前半部分序列字典序更小的选择。
所以 8 5 7 一定会放在末尾。
参考代码
#include<bits/stdc++.h>
using namespace std;
#define fi(l,r) for(int i=l;i<=r;++i)
#define ff(i,l,r) for(int i=l;i<=r;++i)
#define ll long long
#define P 998244353
#define N 1000005
ll qpow(ll a,ll b){
ll c=1;
while(b){
if(b&1)c=c*a%P;
b>>=1;
a=a*a%P;
}
return c;
}
ll inv(ll x){return qpow(x,P-2);}
ll fac[N],ifac[N],ans=1,sub=1;
bool apr[N]={0};
#define C(n,m) (fac[n]*ifac[m]%P*ifac[n-m]%P)
int n,kk,a[N],last=1,aprd,las;
int main(){
freopen("ordinary.in","r",stdin);
freopen("ordinary.out","w",stdout);
scanf("%d %d",&n,&kk);
fi(1,kk){
scanf("%d",&a[i]);
apr[a[i]]=1;
if(a[last]>a[last-1])++last;
}
fac[0]=1;
fi(1,n)fac[i]=fac[i-1]*i%P;
ifac[n]=inv(fac[n]);
for(int i=n-1;i>=1;--i)ifac[i]=ifac[i+1]*(i+1)%P;
ans=fac[n]*ifac[kk]%P;
fi(1,n){
if(apr[i]==0){
while(las<last&&a[las+1]<i)++las;
sub=sub*(las+aprd)%P;
++aprd;
}
}
printf("%lld\n",(ans%P-sub%P+P)%P);
return 0;
}
T2
这不比 T1 简单？
先建括号树，节点的编号 \(i\) 对应着原序列从左往右数第 \(i\) 个左括号（及其对应的右括号）。
对于括号序列
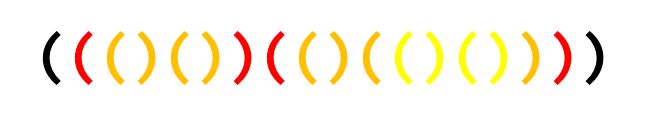
我们分析一下如何操作才能得出序列 ()()()()()()()()()：
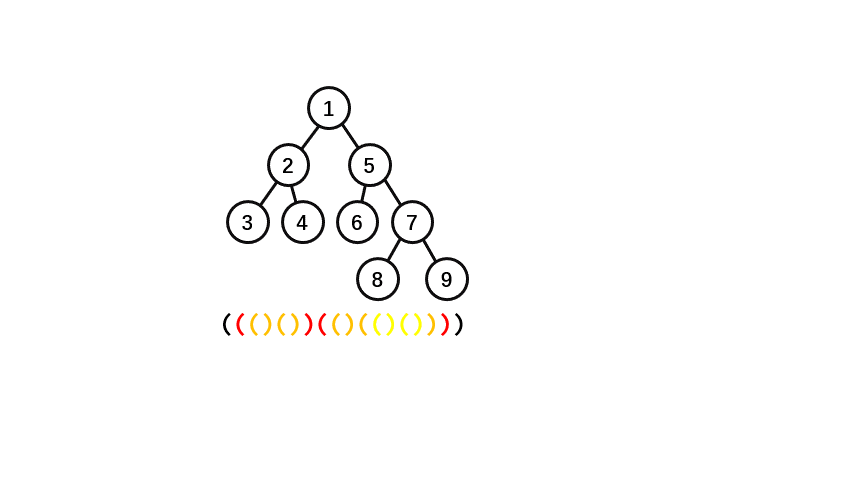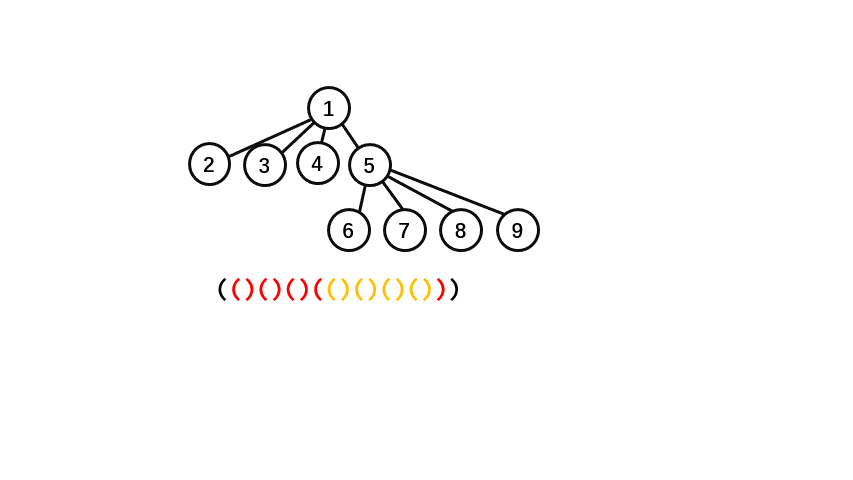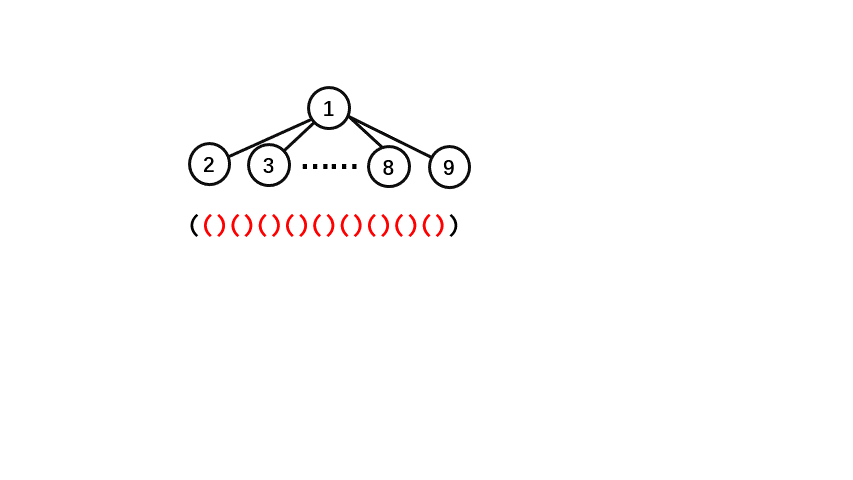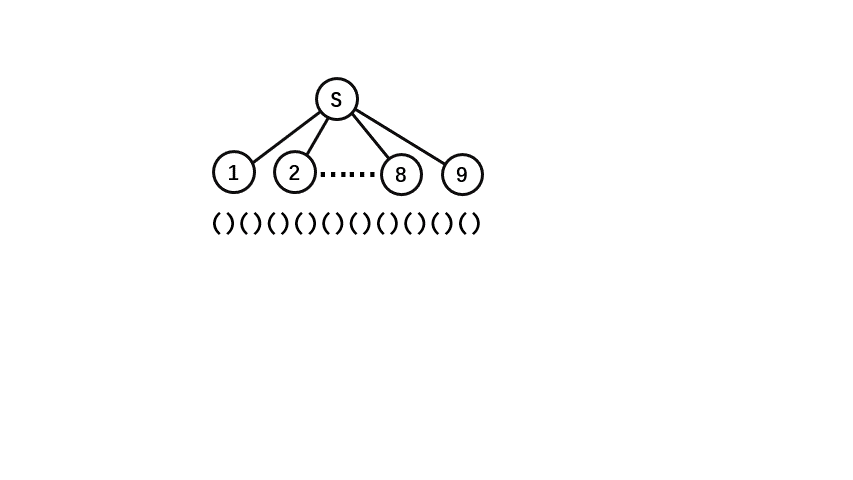
有几步转换不止一个操作。
我们发现只需要 \(8\) 步就行了。
而且仔细观察动画，我们发现将 \(D\) 序列转换为 \(F\) 序列就是把链变成菊花图。
将 \(F\) 转换为 \(D\) 就是把菊花图转化为链。
更细致地观察，我们发现：一个菊花带上父节点需要 \(2\) 步操作才能让父节点也变进菊花里面。
一个链带上父节点需要 \(1\) 步操作可以把父节点和链变成一朵菊花。
所以我们大胆推出结论：原括号树中一个菊花对应需要 \(2\) 步操作，一个链对应需要 \(1\) 步操作，只需要把菊花和链的个数加起来就是变成大菊花图的步数，即：把每个点的贡献加起来：
#define fi(l,r) for(int i=l;i<=r;++i)
void work(int t){
fi(1,n){
if(scnt[t][i]>1)ans[t]+=2;//菊花图：ans+2
else if(scnt[t][i]==0&&scnt[t][fah[t][i]]==1)++ans[t];//链：ans+1
}
}
接下来我们考虑两个括号序列之间的转化：
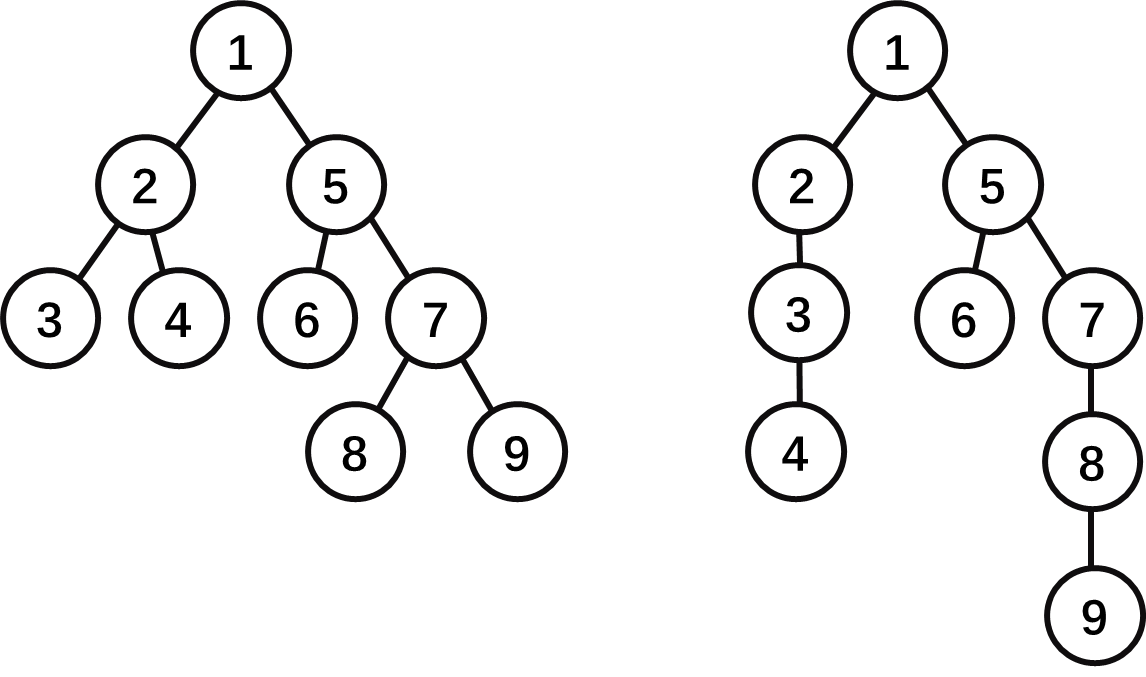
通法当然可以将两棵树都转化为 ()()()()()()()()() ，但这并不保证最优解，我们考虑哪些地方是重复操作的。
注意到当两颗树的 \(5\) 子树操作都完成以后，\(5\) 子树就不用动了，不需要转化为平凡序列，因为两颗子树已经相同。
同样的， \(2\) 子树也不需要进一步地操作。
即：我们可以保留 \(1,2,5\) 的结构不动，不计算这三个点的贡献。
显然，当子树包含相同的节点的时候才会保留，那么如何 \(O(n)\) 求出所有节点是否保留呢？（考试的时候就是在这里寄掉了）
其实我们只需要统计子树大小就行了，因为这棵树的节点编号与 dfs 序是一致的，所以任意子树的节点形成的有序序列一定完全等价于升序序列 \([i,i+siz_i-1]\)。
对了，还有一个条件就是父亲要相同而且父亲也要是相等的节点，不然子树也会被父亲尝试趋同的操作而被打乱。
#define fi(l,r) for(int i=l;i<=r;++i)
#define ff(i,l,r) for(int i=l;i<=r;++i)
#define fab(sth) ff(t,0,1)
for(int i=n;i>=1;--i)
fab()
siz[t][fah[t][i]]+=siz[t][i];
fi(1,n)
if(fah[0][i]==fah[1][i]&&sam[fah[0][i]]==1&&siz[0][i]==siz[1][i])sam[i]=1;
参考代码
查看代码
#include<bits/stdc++.h>
using namespace std;
#define fi(l,r) for(int i=l;i<=r;++i)
#define ff(i,l,r) for(int i=l;i<=r;++i)
#define ll long long
#define N 500005
#define M 1000005
int fah[2][N],n,L,pcnt,stk[N],stl,posofp[M],posof[M],scnt[2][N],ans[3],siz[2][N];//ans2
bool sam[N]={0};
#define fab(sth) ff(t,0,1)
void nothing(int t){
char ch=getchar();
while(ch!='(')ch=getchar();
fi(1,L){
stk[++stl]=(ch=='(');
posof[stl]=i;
if(ch=='(')posofp[i]=++pcnt;
else while(stk[stl-1]==1&&stk[stl]==0){
fah[t][posofp[posof[stl-1]]]=posofp[posof[stl-2]];
++scnt[t][posofp[posof[stl-2]]];
stl-=2;//解析括号序列并建树：将栈顶的 fah 指向下一个元素
}
ch=getchar();
}
if(t==1){
for(int i=n;i>=1;--i)fab()siz[t][fah[t][i]]+=siz[t][i];
fi(1,n)if(fah[0][i]==fah[1][i]&&sam[fah[0][i]]==1&&siz[0][i]==siz[1][i])sam[i]=1;
}
fi(1,n){
if(sam[i]==1){
if(scnt[0][i]>1)ans[2]+=2;//菊花图：ans+2
else if(scnt[0][i]==0&&scnt[0][fah[0][i]]==1)++ans[2];//链：ans+1
}else{
if(scnt[t][i]>1)ans[t]+=2;//菊花图：ans+2
else if(scnt[t][i]==0&&scnt[t][fah[t][i]]==1)++ans[t];//链：ans+1
}
}
}
int main(){
freopen("miracle.in","r",stdin);
freopen("miracle.out","w",stdout);
scanf("%d",&L);
n=L>>1;sam[0]=1;
fi(1,n)siz[0][i]=siz[1][i]=1;
nothing(0);
stl=pcnt=0;
nothing(1);
printf("%d\n",ans[0]+ans[1]-ans[2]);
return 0;
}
说在后面
先谈一谈我对巴以战争的看法吧
