二分图博弈 - 二分图·博弈
二分图·博弈
顾名思义 : 二分图 + 博弈
二分图
首先先知道一些基本方法：
-
求出二分图最大匹配所必须的点或边，就是求去掉这个点（边）过后最大匹配还是不是原来的最大匹配。
复杂度更优的方法是先跑一遍 Dinic 求出最大流的任意解与这种解下每条边的残量。分别从原点、汇点开始 tarjan 残量不为 \(0\) 的边，然后判环，所有与原点或汇点在同一个环里的点一定不是必须匹配点。
比如这个例子：
我们保留所有残量不为 \(0\) 的有向边：
然后分别从 \(S\) 和 \(T\) 跑一遍 Tarjan: (浅色边为环上的边)
因此 \(2,3,4,5\) 号点虽然是最大匹配点，但都不是必须点。
-
在二分图最大匹配中，任意最大匹配边的两个端点所连接的其他非匹配点最多只有 \(1\) 个，不然就会有更大的匹配，如图：
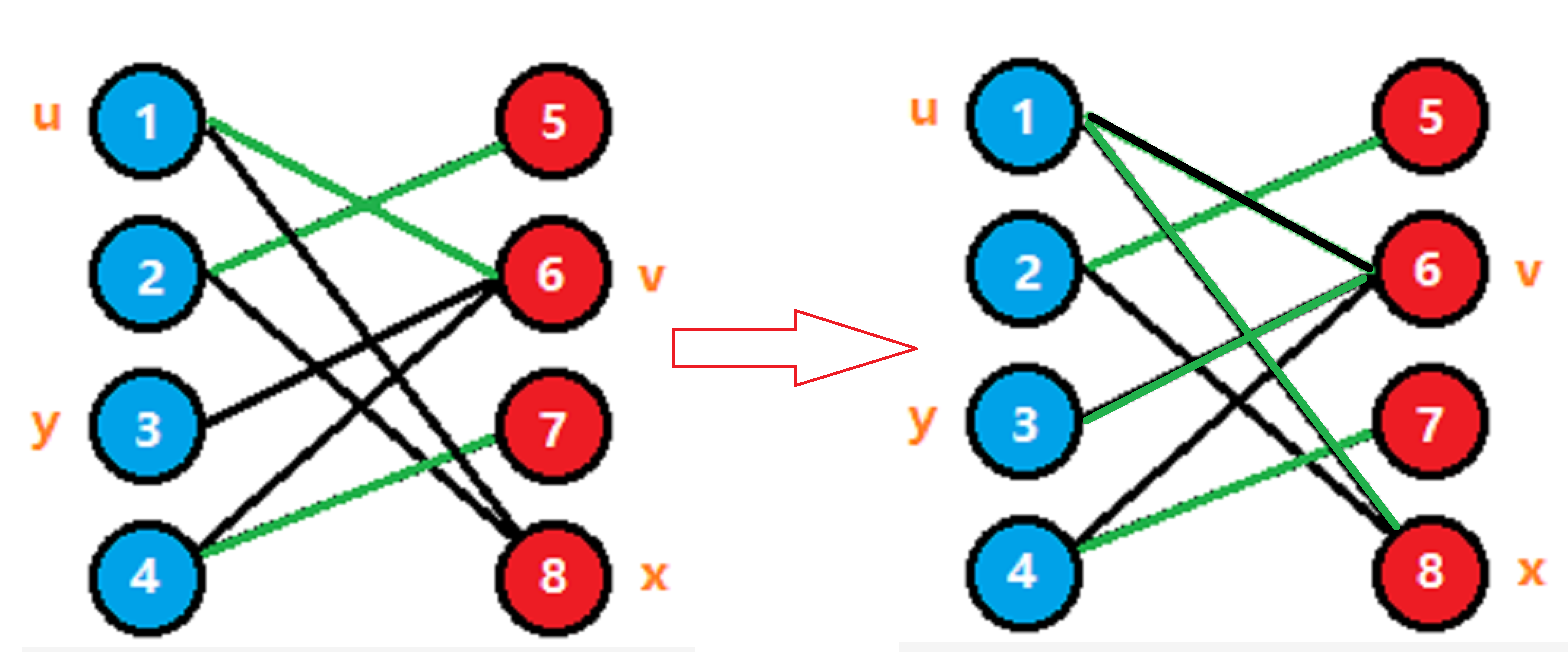
(该图片来自网络)
-
二分图最小点覆盖（就是选几个点使任意边至少有一个端点处于点集中）的点集大小 \(=\) 二分图最大匹配
二分图最小边覆盖（就是选几个点使任意点至少有一个连边处于边集中）的边集大小 \(=\) 非孤立点总数 \(-\) 二分图最大匹配
二分图最小独立点集（就是选几个点使任意边最多只有一个端点处于点集中）的大小 \(=\) 总点数 \(-\) 最小点覆盖 \(=\) 总点数 \(-\) 最大匹配
事实上这三个公式对任意无向图都成立。
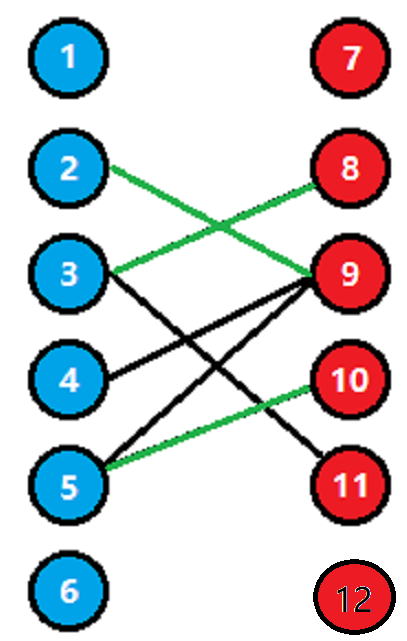
(该图片来自网络)
博弈
知道了二分图怎么求最大匹配必须点集，博弈就简单了。
-
与网格路径有关的题可以给网格黑白染色，连黑白格建二分图。
-
二分图博弈的必胜点就是所有最大匹配均需要的格。证明如下
假设在除去当前点后仍存在一个最大匹配，那我们从当前点必然只能沿非匹配边（如果没有，就说明输了）走向另一端的一个点，而另一端的点必然能够通过一条匹配边（必然存在，否则就不是最大匹配了）走回来。
也就是说，从这边不一定能找到一条边过去，但从那边却一定能找到一条边回来，显然某一刻无法再过去，那么就输了。
-
请完成阅读的同学们完成以下例题：
以下是一份标准的二分图博弈代码（题目：棋盘游戏）
/*
bug:1.tot 不能初始化为 1 因为 e=0 代表没有边
2.是非最大匹配必须点必胜而不是最大匹配必须点必胜，因为是 B 先移动棋子
*/
#include<bits/stdc++.h>
using namespace std;
#define N 105
#define P 100005
#define Q 200005
#define inf 0x3f3f3f3f
int mp[N][N],n,m,tot=1,fir[P],nxt[Q],to[Q],w[Q];
static const int fac[4][2]={{0,1},{0,-1},{-1,0},{1,0}};
pair<int,int>ans[P];
int anscnt;
void add(int x,int y,int z){
nxt[++tot]=fir[x];
fir[x]=tot;
to[tot]=y;
w[tot]=z;
}
int pos2id(int x,int y){
return (y-1)*m+x;
}
int dep[P],S,T;
bool bfs(){
for(int i=pos2id(1,1);i<=T;++i)dep[i]=inf;
queue<int>q;
q.push(S);
dep[S]=0;
while(!q.empty()){
int x=q.front();q.pop();
for(int e=fir[x];e;e=nxt[e]){
int u=to[e];
if(dep[u]>dep[x]+1&&w[e]>0){
dep[u]=dep[x]+1;
q.push(u);
if(u==T)return 1;
}
}
}
return 0;
}//网络流标准的 bfs
int dinic(int x,int flow){
if(x==T)return flow;
int totf=0;
for(int e=fir[x];e;e=nxt[e]){
int u=to[e];
if(dep[u]==dep[x]+1&&w[e]>0){
int newf=dinic(u,min(flow,w[e]));
if(newf==0)continue;
totf+=newf;
w[e]-=newf;
w[e^1]+=newf;
if(totf==flow)return flow;
}
}
return totf;
}//网络流标准的 dinic
int bel[P],dfn[P],low[P],dfc,stk[P],stl;//bel 代表 x 点所处的环的根节点编号
bool ins[P]={0},piped[P]={0};//piped[x] 代表 x 是否是最大匹配点，不一定必须
void tarjan(int x){
dfn[x]=low[x]=++dfc;
ins[x]=1;stk[++stl]=x;bel[x]=x;
for(int e=fir[x];e;e=nxt[e]){
if(w[e]==0)continue;
int u=to[e];
if(dfn[u]==0){
tarjan(u);
low[x]=min(low[x],low[u]);
}else
if(ins[u])low[x]=min(low[x],dfn[u]);
}
if(dfn[x]==low[x]){
for(int u=stk[stl];u!=x;u=stk[--stl])ins[u]=0,bel[u]=x;
--stl,ins[x]=0;
}
return;
}//标准的 tarjan
char ch;
int main(){
scanf("%d %d",&n,&m);
for(int y=1;y<=n;++y){
ch=getchar();while(ch!='#'&&ch!='.')ch=getchar();
for(int x=1;x<=m;++x){
mp[x][y]=(ch=='#');
ch=getchar();
}
}
int nx,ny;
for(int y=1;y<=n;++y){
for(int x=1+(y&1);x<=m;x+=2){
if(mp[x][y]==1)continue;
for(int f=0;f<4;++f){
nx=x+fac[f][0],ny=y+fac[f][1];
if(mp[nx][ny]==0&&nx>0&&nx<=m&&ny>0&&ny<=n){
add(pos2id(x,y),pos2id(nx,ny),1);
add(pos2id(nx,ny),pos2id(x,y),0);
}
}
}
}
S=pos2id(m,n)+1;T=S+1;
for(int y=1;y<=n;++y){
for(int x=1;x<=m;++x){
if(mp[x][y]==1)continue;
if((x+y)&1){
add(S,pos2id(x,y),1);//S -> 左部点
add(pos2id(x,y),S,0);
}else{
add(pos2id(x,y),T,1);//右部点 -> T
add(T,pos2id(x,y),0);
}
}
}//加边
while(bfs())dinic(S,inf);//网络流跑出最大匹配
for(int e=fir[S];e;e=nxt[e])if(w[e]==0)piped[to[e]]=1;//左部匹配点
for(int e=fir[T];e;e=nxt[e])if(w[e]!=0)piped[to[e]]=1;//右部匹配点
tarjan(S);
if(dfn[T]==0)tarjan(T);//Tarjan
for(int y=1;y<=n;++y)
for(int x=1;x<=m;++x)
if(mp[x][y]==0&&(piped[pos2id(x,y)]==0||bel[pos2id(x,y)]==T-((x+y)&1)))//不是最大匹配点或者在环上
ans[++anscnt]={y,x};
printf("%d\n",anscnt);
sort(ans+1,ans+anscnt+1);
for(int i=1;i<=anscnt;++i)printf("%d %d\n",ans[i].first,ans[i].second);
return 0;
}
