割边+割点 学习心得
先背诵 tarjan 板子
#include<bits/stdc++.h>
using namespace std;
#define N 10005
#define M 100005
int tot,first[N],nxt[M],to[M];
void add(int x,int y){
nxt[++tot]=first[x];
first[x]=tot;
to[tot]=y;
}
int n,m;
bool ins[N];
int dfn[N],low[N],dfc,stk[N],stail,idx,siz;
void tarjan(int x){
dfn[x]=low[x]=++dfc;
stk[++stail]=x;
ins[x]=1;
for(int e=first[x];e;e=nxt[e]){
if(!dfn[to[e]]){
tarjan(to[e]);
low[x]=min(low[x],low[to[e]]);
}else if(ins[to[e]]){
low[x]=min(low[x],dfn[to[e]]);
}
}
if(dfn[x]==low[x]){
siz=0;
while(stk[stail]!=x){
--stail;
++siz;
}
--stail;
if(siz>=1)++idx;
}
return;
}
int main(){
memset(ins,0,sizeof ins);
int x,y;
scanf("%d %d",&n,&m);
for(int i=1;i<=m;++i){
scanf("%d %d",&x,&y);
add(x,y);
}
for(int i=1;i<=n;++i){
if(!dfn[i])tarjan(i);
}
printf("%d\n",idx);
return 0;
}
割点
相当于在 tarjan 找完新点以后判断一下新的点能不能通过另一条路径走回来，如果不能，那就是割点。
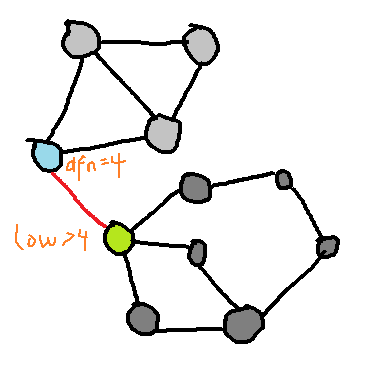
如图所示，下面部分的点，除了红色路径以外就不能走回上面 \(dfn\le4\) 的部分了，因此浅蓝色的点是割点。
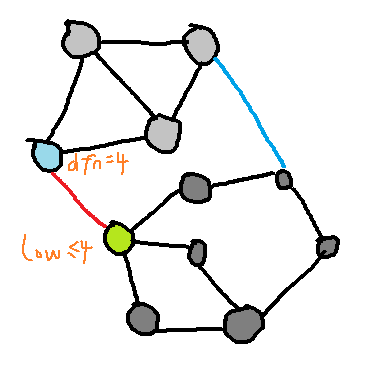
如图所示，如果加了一条蓝色边，那么绿色点就可以通过蓝色边走回来，因此绿色点的 \(low\) 一定小于等于 \(4\) ，即能回到浅蓝色点及其之前的点上去，因此浅蓝色点不是割点。
需要注意的是，每次遍历的根节点不适用于这套规则，需要特判。而根节点是割点的条件是 出度 \(\ge2\) ，很好理解。
/*
bug:low[u] **>= ** 而不是 > dfn[x],因为走得到自己也算。
*/
#include<bits/stdc++.h>
using namespace std;
#define N 20005
#define M 200005
int tot,fir[N],nxt[M],to[M];
int n,m,ans;
int dfn[N],low[N],stk[N],stl,idx,grp[N],spc[N],dfc,root;
bool ins[N];
void add(int x,int y){
nxt[++tot]=fir[x];
fir[x]=tot;
to[tot]=y;
}
void tarjan(int x,int fa){
dfn[x]=low[x]=++dfc;
ins[x]=true;
stk[++stl]=x;
int scnt=0;
for(int e=fir[x];e;e=nxt[e]){
int u=to[e];
if(u==fa)continue;
if(!dfn[u]){
++scnt;
tarjan(u,x);
low[x]=min(low[x],low[u]);
if(low[u]>=dfn[x]&&x!=root){
spc[x]=1;
}
}else if(ins[u]){
low[x]=min(low[x],dfn[u]);
}
}
if(dfn[x]==low[x]){
for(int u;stk[stl]!=x;--stl){
u=stk[stl];
ins[u]=0;
}
ins[x]=0;
--stl;
}
if(x==root){
if(scnt>1)spc[x]=1;
}
return;
}
int main(){
int x,y;
scanf("%d %d",&n,&m);
for(int i=1;i<=m;++i){
scanf("%d %d",&x,&y);
add(x,y);
add(y,x);
}
for(int i=1;i<=n;++i){
if(!dfn[i]){
root=i;
tarjan(i,0);
}
}
for(int i=1;i<=n;++i){
if(spc[i])++ans;
}
printf("%d\n",ans);
for(int i=1;i<=n;++i){
if(spc[i])
printf("%d ",i);
}
return 0;
}
割边
比割点多一个条件：
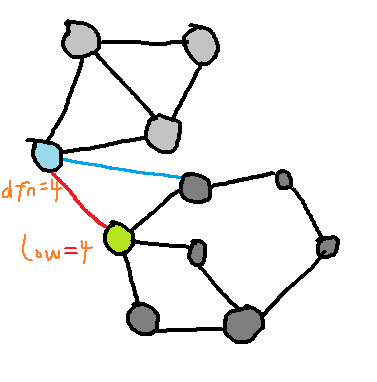
如图，割边不能让另一个边连到浅蓝色节点上，因此判断的条件不是 \(dfn_x \le low_x\) 而是 \(dfn_x < low_x\)
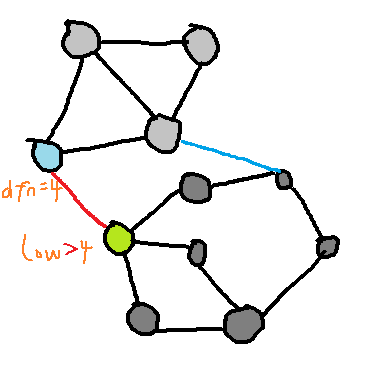
这样就可以了。
并且，算割边不用判断根节点，因为根节点不是一条边。
#include<bits/stdc++.h>
using namespace std;
#define N 200
#define M 10005
int tot,fir[N],nxt[M],to[M];
int dfn[N],dfc,low[N],idx,grp[N],stk[N],stl;
pair<int,int>sln[N];
int n,m,slc;
bool ins[N];
void add(int x,int y){
nxt[++tot]=fir[x];
fir[x]=tot;
to[tot]=y;
}
void tarjan(int x,int fa){
dfn[x]=low[x]=++dfc;
ins[x]=1;
stk[++stl]=x;
for(int e=fir[x];e;e=nxt[e]){
int u=to[e];
if(u==fa)continue;
if(!dfn[u]){
tarjan(u,x);
low[x]=min(low[x],low[u]);
if(low[u]>dfn[x])sln[++slc]=make_pair(min(x,u),max(x,u));
}else if(ins[u]){
low[x]=min(low[x],dfn[u]);
}
}
if(dfn[x]==low[x]){
for(int u;stk[stl]!=x;--stl){
u=stk[stl];
ins[u]=0;
}
ins[x]=0;
--stl;
}
return;
}
int main(){
int x,y;
memset(ins,0, sizeof ins);
scanf("%d %d",&n,&m);
for(int i=1;i<=m;++i){
scanf("%d %d",&x,&y);
add(x,y);
add(y,x);
}
for(int i=1;i<=n;++i){
if(!dfn[i])tarjan(i,0);
}
sort(sln+1,sln+slc+1);
for(int i=1;i<=slc;++i){
printf("%d %d\n",sln[i].first,sln[i].second);
}
return 0;
}
