Fire Net(HDU-1045)(匈牙利最大匹配)(建图方式)
题意
有一个 n*n 的图,. 代表空白区域,X 代表墙,现在要在空白区域放置结点,要求同一行同一列只能放一个,除非有墙阻隔,问最多能放多少个点
思路
只有在墙的阻隔情况下,才会出现一行/列出现多个点的情况,那么可以考虑进行缩点,将同一行且没有墙体阻隔的区域缩成一个点,放到左点集中,将同一列且没有墙体阻隔的区域缩成一个点,放到右点集中,从而建成一个二分图
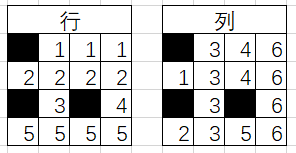
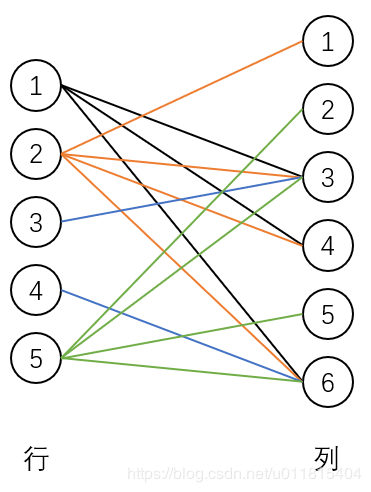
假设 i 为行编号,j 为列编号,若 i-j 之间存在一条边,就相当于在方格 (i,j) 上放了一个点,这个假设使得在没有墙体阻隔的情况下,i 行 j 列不能再放其他的点,那么在不考虑 不能同行同列 的情况下,将所有边连接起来,即行列缩点后,对应方格编号连边
建好图后,在图上求最大匹配即可
C++代码一

#include<iostream> #include<cstdio> #include<cstdlib> #include<string> #include<cstring> #include<cmath> #include<ctime> #include<algorithm> #include<utility> #include<stack> #include<queue> #include<vector> #include<set> #include<map> #define PI acos(-1.0) #define E 1e-9 #define INF 0x3f3f3f3f #define LL long long const int MOD=1E9+7; const int N=1000+5; const int dx[]={-1,1,0,0}; const int dy[]={0,0,-1,1}; using namespace std; int n;//n行n列 bool vis[N];//vis[i]表示是否在交替路中 int link[N];//存储连接点 int G[N][N];//存边 char str[N][N]; int x[N][N],cntX;//行点集 int y[N][N],cntY;//列点集 bool dfs(int x){ for(int y=0;y<cntY;y++){//对x的每个邻接点 if(G[x][y]==1&&!vis[y]){//不在交替路中 vis[y]=true;//放入交替路 if(link[y]==-1 || dfs(link[y])){//如果是未匹配点,说明交替路是增广路 link[y]=x;//交换路径 return true;//返回成功 } } } return false;//不存在增广路,返回失败 } int hungarian(){ int ans=0;//记录最大匹配数 memset(link,-1,sizeof(link)); for(int i=0;i<cntX;i++){//从左侧开始每个结点找一次增广路 memset(vis,false,sizeof(vis)); if(dfs(i))//找到一条增广路,形成一个新匹配 ans++; } return ans; } int main(){ while(scanf("%d",&n)!=EOF&&n){ memset(x,0,sizeof(x)); memset(y,0,sizeof(y)); memset(G,false,sizeof(G)); for(int i=0;i<n;i++) scanf("%s",str[i]); //对行缩点 cntX=1; for(int i=0;i<n;i++){//第i行 for(int j=0;j<n;j++){//第j列 if(str[i][j]=='.')//同一区域 x[i][j]=cntX; if(str[i][j]=='X')//墙体阻隔 cntX++; } cntX++;//下一行 } //对列缩点 cntY=1; for(int j=0;j<n;j++){//第j列 for(int i=0;i<n;i++){//第i行 if(str[i][j]=='.')//同一区域 y[i][j]=cntY; if(str[i][j]=='X')//墙体阻隔 cntY++; } cntY++;//下一列 } //连边 for(int i=0;i<n;i++) for(int j=0;j<n;j++) if(str[i][j]=='.') G[x[i][j]][y[i][j]]=true; printf("%d\n",hungarian()); } return 0; }
C++代码二

#include <bits/stdc++.h> using namespace std; int n; struct node { int a = 0 , b = 0; }; node id[6][6]; char mp[6][6]; bool link[105][105]; bool vis[105]; int use[105]; int hcnt,rcnt; void dfsh(int x,int y){ if(y <= n && mp[x][y] == '.'){ id[x][y].a = hcnt; dfsh(x,y+1); } } void dfsr(int x,int y){ if(x <= n && mp[x][y] == '.'){ id[x][y].b = rcnt; dfsr(x+1,y); } } int find(int x) { for (int s = 1; s < rcnt; s++) { if (link[x][s] && !vis[s]) { vis[s] = 1; if (use[s] == 0 || find(use[s])) { use[s] = x; return 1; } } } return 0; } int main(int argc, char const *argv[]) { while(cin >> n && n){ for(int i = 1;i <= n ;i ++){ cin >> mp[i] + 1; } memset(id,0,sizeof id); memset(link,0,sizeof link); memset(use,0,sizeof use); hcnt = rcnt = 1; for(int i = 1;i <= n;i ++){ for(int j = 1;j <= n ;j ++){ if(mp[i][j] == 'X'){ continue; } if(id[i][j].a == 0){ dfsh(i,j); hcnt ++; } if(id[i][j].b == 0){ dfsr(i,j); rcnt ++; } link[id[i][j].a][id[i][j].b] = 1; } } int sum = 0; for(int i = 1;i < hcnt;i ++){ memset(vis,0,sizeof vis); if(find(i)) sum ++; } printf("%d\n",sum ); } return 0; }
C++代码三

#define N 6 #include<queue> #include<stdio.h> #include<string.h> #include<algorithm> using namespace std; char k[N][N]; int book[N][N]; int n,ma; void dfs(int step) { if(step>ma)//保留每次能放得最大碉堡数 { ma=step; return; } for(int i=0; i<n; i++) { for(int j=0; j<n; j++) { if(k[i][j]=='.'&&!book[i][j])//如果这个位置可以放碉堡 { int a=i,b=i,c=j,d=j; //向四个方向覆盖,遇到边界或墙停止 while(a>=0&&k[a][j]=='.'){book[a][j]++;a--;} while(b<n&&k[b][j]=='.'){book[b][j]++;b++;} while(c>=0&&k[i][c]=='.'){book[i][c]++;c--;} while(d<n&&k[i][d]=='.'){book[i][d]++;d++;} dfs(step+1);//放置的碉堡数加1 a=i,b=i,c=j,d=j; //取消覆盖 while(a>=0&&k[a][j]=='.'){book[a][j]--;a--;} while(b<n&&k[b][j]=='.'){book[b][j]--;b++;} while(c>=0&&k[i][c]=='.'){book[i][c]--;c--;} while(d<n&&k[i][d]=='.'){book[i][d]--;d++;} } } } return; } int main() { while(scanf("%d",&n)&&n) { for(int i=0; i<n; i++) scanf("%s",k[i]); memset(book,0,sizeof(book)); ma=0; dfs(0); printf("%d\n",ma); } return 0; }



 浙公网安备 33010602011771号
浙公网安备 33010602011771号