【BZOJ1294】[SCOI2009]围豆豆Bean 射线法+状压DP+SPFA

首先说一下什么叫射线法。
射线法就是从一个点向右做一条射线，如果与路线的交点个数为奇数，则这个点一定被围起来了。
举几个例子：

这是有一个交点的情况。

 

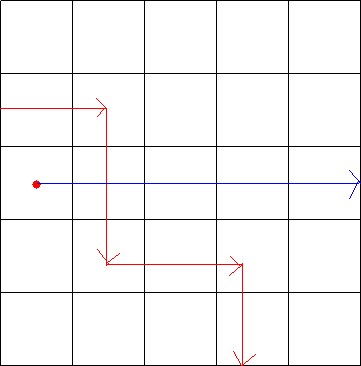
这是有三个交点的情况。

 

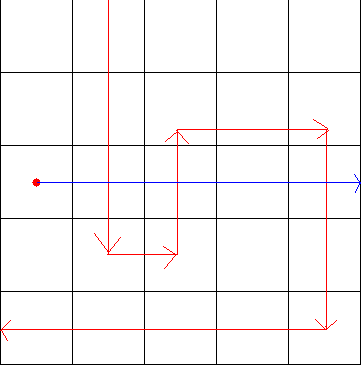
这是有两个交点的情况，如图所示点没有被围起来。

 

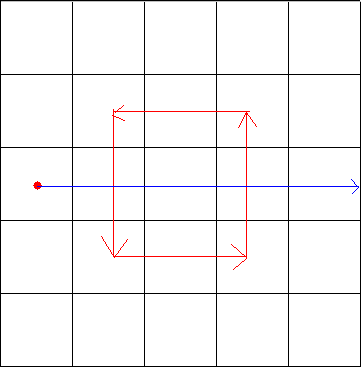
但还有一种情况，在偶数个交点时也有可能被围起来。如下图所示：

 

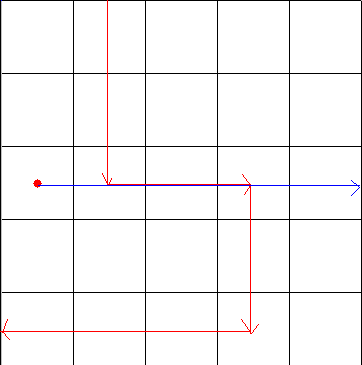
也就是说，如果两条相交的边同向，也有可能会包围点。
范围较小，考虑状压DP，fi,j,kfi,j,k表示从点(i,j)(i,j)出发当前豆豆的二进制表示下状态为kk的收益，那么我们可以一遍spfa进行转移，如果回到了点(i,j)(i,j)则更新答案。
那么转移的过程中，显然水平方向的移动是不影响答案的，只有竖直方向的移动才会影响到点的位置，那么因为刚才说了一种特殊情况，我们要不要记录方向呢？其实可以转化一下，把每一条线段假设成上端为开下端为闭的线段，即只有下断点与射线相交才会有用，那么这样同向的线段就只会被算一次了。完美解决了这个问题。

题解

 

我们可以枚举起点，用f[a][b][S]表示当前走到(a,b)，已经围住的豆豆状态为S的最短路。转移因为存在环，所以要用SPFA。但是问题在于，如何判断一个豆豆是否被我们围住了呢？

这里采用射线法：我们从每个豆豆向右引一条射线，如果这条射线与路径有奇数个交点则被围住，否则不被围住。但是可能存在我们顺着射线走的情况。于是将射线向下移动半格即可。

 

C++代码

#include <cstdio>
#include <cstring>
#include <iostream>
#include <queue>
using namespace std;
const int maxn=(1<<9)+3;
int f[10][10][maxn],val[maxn];
int inq[10][10][maxn],v[10],tr[10][10],dx[]={1,0,-1,0},dy[]={0,1,0,-1};
char s[10][10];
queue<int> q1,q2,q3;
int n,m,K,ans;
int S;
int a,b,c,d,T;
int main(){
    int n , m , q;
    cin >> n >> m >> q;
    for(int i = 0;i < q; i ++) cin >> v[i];
    
    for(int i = 1;i < (1 << q); i++){
        for(int j = 0;j < q ; j ++){
            if((i >> j) & 1){
                val[i] = val[i ^ (1 << j)] + v[j];
                break;
            }
        }
    }
    
    for(int i = 0;i < n; i++){
        scanf("%s",s[i]);
        S = 0;
        for(int j = 0;j < m; j ++){
            if(s[i][j] >= '1' && s[i][j] <= '9') S |= 1 << (s[i][j] - '1');
            tr[i][j] = S;
        }
    }
    
    for(int i = 0; i < n;i ++) for(int j = 0; j < m ; j++) if(s[i][j] == '0'){
        memset(f,0x3f,sizeof f);
        f[i][j][0] = 0;
        q1.push(i); q2.push(j); q3.push(0);
        while(!q1.empty()){
            a = q1.front() ; b = q2.front(); S = q3.front();
            inq[a][b][S] = 0;q1.pop(),q2.pop(),q3.pop();
            if(a == i && b == j){
                ans = max(val[S] - f[a][b][S],ans);
            //    cout << val[S] << endl;
            }
            for(int k = 0;k < 4;k ++){
                c = a + dx[k];
                d = b + dy[k];
            
            if(c<0||c==n||d<0||d==m||s[c][d]!='0')    continue;
                    T = S;
                if(k == 0) T ^= tr[a][b];
                if(k == 2) T ^= tr[c][d];
                if(f[c][d][T] > f[a][b][S] + 1){
                    f[c][d][T] = f[a][b][S] + 1;
                    if(!inq[c][d][T]) inq[c][d][T] = 1,q1.push(c),q2.push(d),q3.push(T);
                }
            }
            
        }
    }
    printf("%d",ans);
}