前向星和链式前向星
1、前向星
前向星是以存储边的方式来存储图，先将边读入并存储在连续的数组中，然后按照边的起点进行排序，这样数组中起点相等的边就能够在数组中进行连续访问了。它的优点是实现简单，容易理解，缺点是需要在所有边都读入完毕的情况下对所有边进行一次排序，带来了时间开销，实用性也较差，只适合离线算法。图一-2-4展示了图一-2-1的前向星表示法。
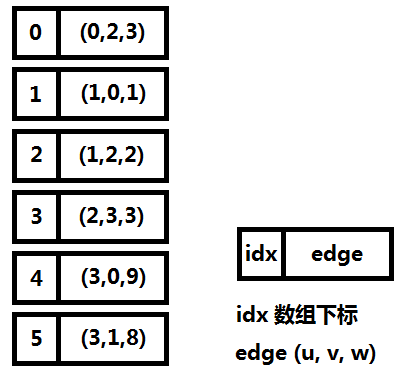
2、链式前向星（就是数组模拟链表）
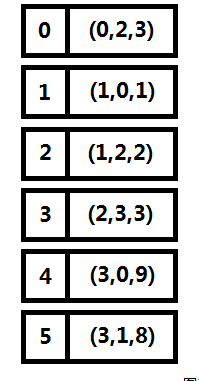
链式前向星和邻接表类似，也是链式结构和线性结构的结合，每个结点i都有一个链表，链表的所有数据是从i出发的所有边的集合（对比邻接表存的是顶点集合），边的表示为一个四元组(u, v, w, next)，其中(u, v)代表该条边的有向顶点对，w代表边上的权值，next指向下一条边。
具体的，我们需要一个边的结构体数组 edge[MAXM]，MAXM表示边的总数，所有边都存储在这个结构体数组中，并且用head[i]来指向 i 结点的第一条边。
边的结构体声明如下：
struct EDGE {
int u, v, w, next;
EDGE() {}
EDGE(int _u, int _v, int _w, int _next) {
u = _u, v = _v, w = _w, next = _next;
}
}edge[MAXM];
int u, v, w, next;
EDGE() {}
EDGE(int _u, int _v, int _w, int _next) {
u = _u, v = _v, w = _w, next = _next;
}
}edge[MAXM];
初始化所有的head[i] = INF，当前边总数 edgeCount = 0
每读入一条边，调用addEdge(u, v, w)，具体函数的实现如下：
void addEdge(int u, int v, int w) {
edge[ edgeCount ] = EDGE(u, v, w, head[u]);
head[u] = edgeCount ++;
}
edge[ edgeCount ] = EDGE(u, v, w, head[u]);
head[u] = edgeCount ++;
}
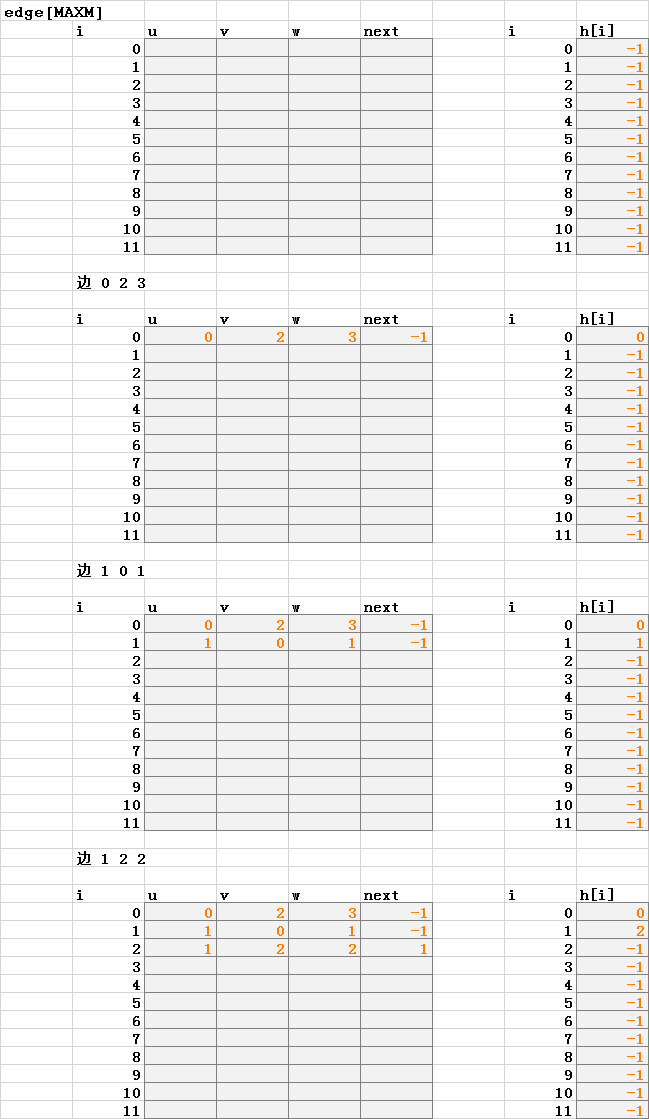
这个函数的含义是每加入一条边(u, v)，就在原有的链表结构的首部插入这条边，使得每次插入的时间复杂度为O(1)，所以链表的边的顺序和读入顺序正好是逆序的。这种结构在无论是稠密的还是稀疏的图上都有非常好的表现，空间上没有浪费，时间上也是最小开销。
调用的时候只要通过head[i]就能访问到由 i 出发的第一条边的编号，通过编号到edge数组进行索引可以得到边的具体信息，然后根据这条边的next域可以得到第二条边的编号，以此类推，直到next域为INF（这里的INF即head数组初始化的那个值，一般取-1即可）。
