矩阵快速幂(Matrix_Fast_Power)
一、基础知识
(1)矩阵乘法
https://blog.csdn.net/weixin_43272781/article/details/82899737
简单的说矩阵就是二维数组,数存在里面,矩阵乘法的规则:A*B=C

其中c[i][j]为A的第i行与B的第j列对应乘积的和,即: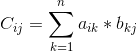
代码:
const int N=100; int c[N][N]; void multi(int a[][N],int b[][N],int n)//n是矩阵大小,n<N { memset(c,0,sizeof c); for(int i=1;i<=n;i++) for(int j=1;j<=n;j++) for(int k=1;k<=n;k++) c[i][j]+=a[i][k]*b[k][j]; }
另一种写法:
int c[N][N]; void multi(int a[][N],int b[][N],int n) { memset(c,0,sizeof c); for(int i=1;i<=n;i++) for(int k=1;k<=n;k++) for(int j=1;j<=n;j++) c[i][j]+=a[i][k]*b[k][j]; }
这种可以在第二重for判断if(a[i][k]==0)continue;对于矩阵有较多0的有一定效果。不过一般第一种写法就够了,这种知道就行。
显然矩阵乘法的复杂度是O(n^3);(O(n^2.7)的方法不会写,无视这里)。
这里我直接写的是n*n的矩阵(即方阵),显然两个相乘是要一行和一列对应乘,那么矩阵乘法是需要A的行数与B的列数相等的(这是A*B的前提条件,可见矩阵的乘法是不满足交换律的)。然而这些一般都是没什么用的,矩阵快速幂只会用到方阵(除非题目是裸的矩阵乘法)。矩阵快速幂都是方阵也就避免的相乘的前提条件,可以放心用。
二、矩阵快速幂
如果不知道快速幂的请参考:https://www.cnblogs.com/DWVictor/p/10278589.html
const int N=10; int tmp[N][N]; void multi(int a[][N],int b[][N],int n) { memset(tmp,0,sizeof tmp); for(int i=0;i<n;i++) for(int j=0;j<n;j++) for(int k=0;k<n;k++) tmp[i][j]+=a[i][k]*b[k][j]; for(int i=0;i<n;i++) for(int j=0;j<n;j++) a[i][j]=tmp[i][j]; } int res[N][N]; void Pow(int a[][N],int n) { memset(res,0,sizeof res);//n是幂,N是矩阵大小 for(int i=0;i<N;i++) res[i][i]=1; while(n) { if(n&1) multi(res,a,N);//res=res*a;复制直接在multi里面实现了; multi(a,a,N);//a=a*a n>>=1; } }
值得注意的是矩阵快速幂只适用于n*n的矩阵方阵。
三、例题
http://poj.org/problem?id=3070
http://poj.org/problem?id=3233
http://acm.hdu.edu.cn/showproblem.php?pid=2276
http://acm.hdu.edu.cn/showproblem.php?pid=5015
https://ac.nowcoder.com/acm/contest/338/L
(题解:https://paste.ubuntu.com/p/8pMmJc6SDn/)


 浙公网安备 33010602011771号
浙公网安备 33010602011771号