函数式编程学习之路(四)
知识点理解一:
函数:
函数（function）表示每个输入值对应唯一输出值的一种对应关系。函数f中对应输入值的输出值x的标准符号为f(x)。包含某个函数所有的输入值的集合被称作这个函数的定义域，包含所有的输出值的集合被称作值域。若先定义映射的概念，可以简单定义函数为，定义在非空数集之间的映射称为函数。
高阶函数:
在数学和计算机科学中，高阶函数是至少满足下列一个条件的函数:
- 接受一个或多个函数作为输入
- 输出一个函数
在数学中它们也叫做算子(运算符)或泛函。微积分中的导数就是常见的例子，因为它映射一个函数到另一个函数。
在无类型 lambda 演算，所有函数都是高阶的；在有类型 lambda 演算（大多数函数式编程语言都从中演化而来）中，高阶函数一般是那些函数型别包含多于一个箭头的函数。在函数式编程中，返回另一个函数的高阶函数被称为Curry化的函数。
柯里化（Currying）:
在计算机科学中，柯里化（Currying），是把接受多个参数的函数变换成接受一个单一参数（最初函数的第一个参数）的函数，并且返回接受余下的参数而且返回结果的新函数的技术。这个技术由 Christopher Strachey 以逻辑学家 哈斯凯尔·加里 命名的，尽管它是 Moses Schönfinkel 和 Gottlob Frege发明的。
不动点:
在数学中，不动点定理是一个结果表示函数F在某种特定情况下，至少有一个不动点存在，即至少有一个点x能令函数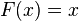
λ演算的共同主题是找到给出λ表达式的不动点。每个λ表达式都有一个不动点，不动点组合子是一个“函数”，即输入一个λ表达式并输出该表达式的一个不动点。一个重要的不动点组合是Y组合子，它使用递归定义。
Y组合子:
在无类型 lambda 演算中众所周知的（可能是最简单的）不动点组合子叫做 Y 组合子。它是 Haskell B. Curry 发现的，定义为
- Y = λf.(λx.f (x x)) (λx.f (x x))用一个例子函数g来展开它，我们可以看到上面这个函数是怎么成为一个不动点组合子的：
- Y g = (λf.(λx . f (x x)) (λx . f (x x))) g
- Y g = (λx. g (x x)) (λx . g (x x)) （λf 的 β-归约 - 应用主函数于 g）
- Y g = (λy. g (y y)) (λx . g (x x)) （α-转换 - 重命名约束变量）
- Y g = g ((λx. g (x x)) (λx . g (x x))) （λy 的 β-归约 - 应用左侧函数于右侧函数）
- Y g = g (Y g) （Y 的定义）
注意 Y 组合子意图用于传名求值策略，因为 (Y g) 在传值设置下会发散（对于任何 g）。
理解这些玩意费脑子,不动点,就是F(x)= x, 例如，0 和 1 是函数 f(x) = x2 的不动点，因为 02 = 0 而 12 = 1.那么lambda演算必然至少有一个不动点,理解就是一个lambda函数,必然会有一个值等于这个把这个值作为参数调用这个函数后的结果(或简单的说,这个函数的运算,必然最少有一个参数等于结果?)
这里头就有一个问题:为什么会这样?如果没有不动点,就是这个函数没有一个输入等于输出,这个函数就不是一个lambda函数,它不能用计算机来计算?
Y组合子,就是一个找出lambda函数的不动点,这样Y(f) = 不动点
鉴于一阶函数（在简单值比如整数上的函数）的不动点是个一阶值，高阶函数 f 的不动点是另一个函数 g 使得 f(g) = g。那么，不动点算子是任何函数 fix 使得对于任何函数 f 都有f(fix(f)) = fix(f).
这里比较晕的就是,这个不动点算子,算的是结果是一个不动点,参数是lambda表达式, 看多大堆符号晕,写成伪代码:
不动点函数(lambda函数)=lambda函数(不动点函数(lambda函数)
用f(x)=x^2为例, 求1, 这里假设function关键字能定义"函数变量"
先算左边
function LambdaFunction =function(x){return x ^ 2};
function YFunction = function(LambdaFunction) {return 神奇的组合子算法};
int i = YFunction(LambdaFunction(1);
这里算出i=1, 即求出了不动点
再算右边
function LambdaFunction =function(x){return x ^ 2};
function YFunction = function(LambdaFunction) {return 神奇的组合子算法};
int i = LambdaFunction(YFunction(LambdaFunction(1));
相当于 i = LambdaFunction(1);
因为1已经是这个函数的不动点,所以LambdaFunction(1)必定等于1
可以算出i = 1
这个神奇的Y组合子,绕来绕去的绕晕了,我们尝试着生活化的表达下看看,能不能理解它.
我们用地图扔地上来举例, Y组合子算法,就是找到和地上接触的那一个不动点.它对应地图和地的刚好相等位置.(左式)
地图扔地上的算法是一个标准Lambda算法(就是说,地图和地是有算法上的关系的,这种关系我们用直觉去思考一下,地图放在地面上)
而一个标准的Lambda算法,就是不点值为参数时,结果值也是和参数相等(白算了)所以Lambda(不动点)=不动点
所以:Y(f) = f(Y(f)),或者fix(f)=f(fix(f))
那么这个神奇的,专门计算Lambda函数的不动点的Y组合子函数有什么用呢?
柯里化（Currying）,这个颗粒化,真是日用而不知,原来我们写函数,就是在颗粒化
高阶函数,输入是函数,输出也是函数,所有的无类型lambda都是高阶(无类型和有类型是什么意思?)
函数,玩了半天,算是找到了熟人,就是一个变化,吃进去的是大米.拉出来的是X.我们人类能感知的世界,都在变化之中,唯一不变的就是变化本身,所以我们的世界是函数的.
待续...
