数据结构及算法基础--快速排序（Quick Sort）（一）
快速算法同样是非常重要的，用我们教授的话，这是一个里程碑的算法。虽然我也不知道为什么。
我们还是首先来看看快速排序的思想：
通过一趟排序将要排序的数据分割成独立的两部分，其中一部分的所有数据都比另外一部分的所有数据都要小，然后再按此方法对这两部分数据分别进行快速排序，整个排序过程可以递归进行，以此达到整个数据变成有序序列。
我们仍然要用到非常重要的递归。
我们给出流程图：
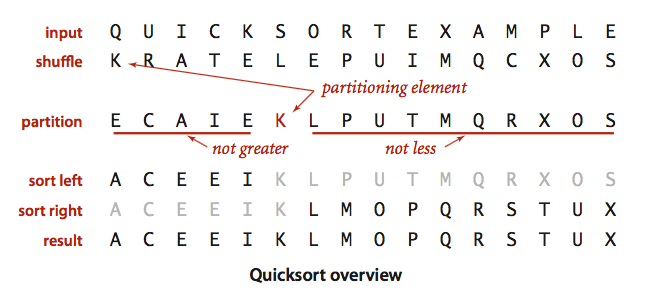
我们可以看到我们进行了suffle的过程，这一步的原因我们在后面关于性能分析的时候会给出。
partition过程便是以分割元素为界限，左边都小于分割元素，右边都大于分割元素。
然后我们在分别对左右进行排序。这便是快速排序的思想：
我们给出代码：
private static int partition(Comparable[] a,int lo,int hi){ int i=lo,j=hi+1; Comparable v=a[lo]; while(true){ while(less(a[++i],v))if(i==hi)break; while(less(v,a[--j]))if(j==lo)break; if(i>=j)break; exch(a,i,j); } exch(a,lo,j); return j; } private static void QuickSort(Comparable[] a){ QuickSort(a,0,a.length-1); } private static void QuickSort(Comparable[] a,int lo,int hi){ if(lo>=hi)return; int j=partition(a,lo,hi); QuickSort(a,lo,j-1); QuickSort(a,j+1,hi); }
注意，上述代码中是没有进行shuffle这一步操作的，这是不会影响排序结果的，shuffle只会影响算法的时间复杂度。
具体分析的话，细节流程如下：
接下来我们重点讲一下上述代码中的partition过程是怎么回事：
我们可以看到我们是将从序列开头和结尾同时向中进行比较，从开头找到比分割元素大的，从结尾找到比分割元素小的，然后交换两个元素，直到i与j相遇：
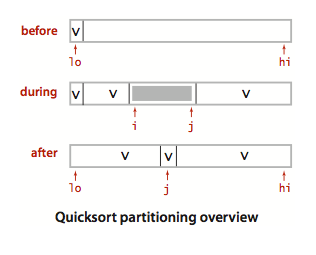
上图中在during过程中，灰色区域为还为partition的部分，此刻在i前面的元素一定比v小，在j后的元素一定比v大。
细节的流程例子如下：
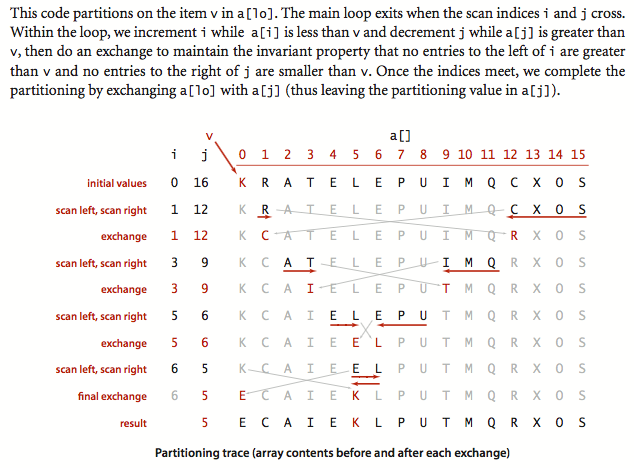
最后再将分割元素与最后一个比其小的元素交换。
性能分析：
1）时间复杂度。
我们考虑时间复杂度还是考虑比较和交换的次数。但是在快速排序中，交换的次数完全取决于序列本身，所以我们无法进行分析。
但是对于比较次数，我们可以进行分析：
首先我们考虑最优情况：
令：n = n/2 = 2 { 2 T[n/4] + (n/2) } + n ----------------第二次递归
= 2^2 T[ n/ (2^2) ] + 2n
令：n = n/(2^2) = 2^2 { 2 T[n/ (2^3) ] + n/(2^2)} + 2n ----------------第三次递归
= 2^3 T[ n/ (2^3) ] + 3n
......................................................................................
令：n = n/( 2^(m-1) ) = 2^m T[1] + mn ----------------第m次递归(m次后结束)
当最后平分的不能再平分时，也就是说把公式一直往下跌倒，到最后得到T[1]时，说明这个公式已经迭代完了（T[1]是常量了）。
得到：T[n/ (2^m) ] = T[1] ===>> n = 2^m ====>> m = logn；
T[n] = 2^m T[1] + mn ；其中m = logn;
T[n] = 2^(logn) T[1] + nlogn = n T[1] + nlogn = n + nlogn ；其中n为元素个数
又因为当n >= 2时：nlogn >= n (也就是logn > 1)，所以取后面的 nlogn；
综上所述：快速排序最优的情况下时间复杂度为：O( nlogn )
这其实也是最优情况下比较的次数 nlogn。
最坏情况：
最差的情况就是每一次取到的元素就是数组中最小/最大的，这种情况其实就是冒泡排序了(每一次都排好一个元素的顺序)
这种情况时间复杂度就好计算了，就是冒泡排序的时间复杂度：T[n] = n * (n-1) = n^2 + n～n^2;
综上所述：快速排序最差的情况下时间复杂度为：O( n^2 )。比较次数则为~n^2;
平均情况：
平均高情况我并没有看懂书中的内容。ORZ,但是我们还是可以根据最优情况类比一下。
结论是：平均使用了2n*ln（n），注意，这里是ln，是自然对数啊。而它约等于1.39nlogn。所以平均比较次数比最优高出39%左右。
而它的算法复杂度则也是O( nlogn ).
因为我也没动这个证明过程，所以我也不进行说明，以免进行误导，但是我给出《algorithm》中的证明过程：
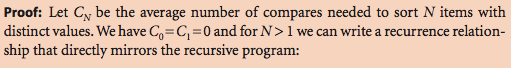
2）空间复杂度：
