详细分析平衡树-红黑树平衡修正 图文详解 (万字长文)
红黑树
简述
红黑树,是一种二叉搜索树,但在每个结点上增加一个存储位表示结点的颜色,可以是Red或Black。 通过对任何一条从根到叶子的路径上各个结点着色方式的限制,红黑树确保没有一条路径会比其他路径长出俩倍,因而是接近平衡的。
性质/规则
详细说明:红黑树_百度百科 (baidu.com)
主要规则:
为了方便理解和记忆,先将红黑树规则分解,以下三点是我认为理解红黑树是最主要的规则.加粗的是关键字,先记住这些关键字,去学习红黑树时会容易理解许多.
- 根节点是黑色.
- 任意两个相邻结点不能同时为红.即红色结点的孩子是黑色的.(不能出现连续的红色结点)
- 任意结点到其可到达的叶节点间,均包含相同数量的黑色结点.(每条路径上都有相同的黑色结点)
其他规则:
默认规则:每个结点不是红色就是黑色
补充:叶结点都是黑色,且不存数据,也被称为NIL结点nil(计算机语言)_百度百科 (baidu.com)
转载:通过将红黑树的所有叶子节点都替换为NIL节点,可以保证红黑树的每个节点都至少有一个子节点,从而简化了操作的实现。NIL节点的存在有助于维护红黑树的结构和性质,特别是在处理边界情况时,通过判断节点的子节点是否为NIL节点来避免特殊处理叶子节点的情况.
推导性质:
推导规则是红黑树规则加二叉树性质推导的一些规则,在后面用来证明和理解红黑树的一些操作.
- 推导性质1:
一条路径的所有可能情况中,最长路径节点个数不会超过最短路径的两倍(连续的红节点能够使最长路径超过最短路径的两倍)
从根到叶子的最长的可能路径不多于最短的可能路径的两倍长。
红色结点如果有两个孩子,则都是黑色.(可能有0,1,2个黑孩子)
修改祖先结点颜色变化不会影响所有分支路径的黑色结点的平衡(修正常用)
- 推导性质2:
-
最短路径:全部是黑色结点
-
最长路径:红黑相间(一黑一红,最后一个非NIL结点可以是红)
-
去掉红色结点的红黑树接近一棵满二叉树.(直接去掉红色结点可能就不是二叉树了,hold不住)
-
当只有一个根节点时(黑),第二个结点只能是红色(满足黑结点数量相同),被迫只能插入红色结点.
-
新增结点默认为红色,红色规则比黑色宽松
- 推导性质3:
设黑色结点有N个
-
最短路径长度为:$log_2(N) $
-
最长路径长度为:$2log_2(N)$
-
一棵红黑树的所有结点数量在[N,2N]之间.(全黑为N,红黑全满为2N)
-
性能上,假设有10亿个结点,AVL树最多查找30次, RB树最多查找60次
注:文章仅以理解红黑树的主要功能(插入修正)实现为主,没有实现对NIL结点处理等其他情况,不是严谨的红黑树实现.
红黑树的基本实现
基本功能和AVL树是几乎一样的.以下就简要描述了
struct RBTreeNode
template<class K, class V>
struct RBTreeNode {
//三叉链
RBTreeNode* _left;
RBTreeNode* _right;
RBTreeNode* _parent;
std::pair<K,V> _kv;
Color _col;
RBTreeNode(const decltype(_kv)& kv)
: _left(nullptr)
,_right(nullptr)
,_parent(nullptr)
,_kv(kv)
,_col(Color::RED) //默认为红,因为规则最宽松
{}
};
class RBTree
enum class Color { RED, BLACK };
template<class K,class V>
class RBTree {
public:
bool Insert(const std::pair<K,V>& kv);
private:
using Node = RBTreeNode<K,V>;
Node* _root;
};
红黑树的插入
插入的重点和AVL树一样,在于插入修正
bool Insert(const std::pair<K,V>& kv) {
if (_root == nullptr) {
_root = new Node(kv);
_root->_col = Color::BLACK;
return true;
}
Node* cur = _root;
Node* parent = _root;
while (cur) {
if (kv.first > cur->_kv.first) {
parent = cur;
cur = cur -> _right;
}
else if (kv.first < cur->_kv.first) {
parent = cur;
cur = cur -> _left;
}
else {
//存在相同的
return false;
}
} //while比较过程 [end]
//没找到,新增
cur = new Node(kv); //cur地址改变,只能使用kv进行比较(始终使用kv就好了)
//维护三叉链
if (cur->_kv->first > parent->_kv.first) {
parent->_right = cur;
}
else {
parent->_left = cur;
}
//检查和调整红黑树
FixInsert();
}
红黑树插入修正前言
在实现红黑树插入前,我们知道红黑树插入新结点后,一定会出现不满足红黑树规则的情况,因此我们先将需要,红黑树的修正操作主要通过旋转和变色来实现.
什么时候需要变色:
只有父亲是红色时,才需要变色,且必须变色.(红节点不相邻规则)
变色的基础:
插入红节点规则最宽松,不需要调整其他路径,因此插入结点不可变色,所以只能将父亲变成黑色,后面就围绕父亲变黑后,爷爷结点和叔叔结点如何变色进行处理.
一句话:父亲是红色时,必须要变色,父亲变成黑色.(另一种说法:都是父爷颜色交换)
为什么需要旋转与变色
变色:
根据二叉树规律:满二叉树总是一个结点两个孩子,总是1:2的关系.
通过这个关系可以实现数量对调操作,即1个黑色父:2个红色孩子 可以转换成 1个红色父:2个黑色孩子

这样变色对父结点的所有分支路径颜色影响比较小,不容易破坏红黑树黑结点数量相同规则(简称).
旋转
首先,1个黑结点,两个红节点.观察发现,只要一定的旋转操作即可平衡.

红黑树在某些情况下,直接变色操作难以满足规则,或者较为复杂;而通过一定地旋转操作后,会更加简单,因此红黑树需要循环.具体情况请看下文.
;另外,具体的旋转操作我在另一篇博客详细描述了,本篇就不再描述太多了.AVL树博客
需要修正的所有情况(以左为例)
红黑树需要修正的所有情况都是从下面这棵抽象树衍生出的.

实际衍生情况对比起AVL树会更加复杂,也不容易描述.
只有理解红黑树基本的修正情况才能够实现红黑树.下面将循序渐进讲解:
先认识最简单的情况
最简单的情况可以认为是最远的几个结点之间的修正,也是插入后第一次修正,最简单情况也是最容易理解的.红黑树修正和AVL树的一样,情况很多很复杂,搞定简单的再去看抽象情况好理解很多.
1. 叔叔是红色结点
描述:叔叔和父亲都是红色,且叔叔和父亲都是非NIL结点的最远结点.
反证:如果叔叔还有子结点,那一定是黑色,即多了一个黑色结点;为了满足各路径黑结点数量相同的规则,父结点也必须要有黑色子节点,且必须要有两个,那就无法再插入新节点了,因此这种情况不可能.
- 左左(LL型)
插入到父结点的左边

操作:父变黑,爷变红(父爷交换颜色),叔叔变黑

感性解释:
父子都是红,只能且必须由父亲变黑.因为多了一个黑结点,所以所在路径必须上少一个黑结点;
要少哪一个呢?肯定不能往下了,因为下面是已经处理过了(修正操作是往上迭代的),所以只能往上寻找;
因为插入前路径上的所有结点都是满足红黑树规则的,所以爷爷结点一定是黑色;又因为爷爷距离父是最近的结点,对其他结点影响最小,因此选择将爷爷结点置为红,即将父爷结点颜色交换;
爷爷颜色是红色结点后,叔叔路径则少了一个黑色结点,因此叔叔结点必须变黑.
- 左右(LR型)
操作:父变黑,爷变红(父爷交换颜色),叔叔变黑.

因为父和叔都是最远结点,调整过程没有子结点影响,也不需要旋转等额外操作,因此和LL型是完全相同的.
注意:
爷爷非根,在有叔叔且为红的情况下,新增结点加一轮修正后,爷爷会变红 此时如果祖爷爷也为红,需要继续修正.
也只有这种情况下才可能需要继续修正
2.没有叔叔结点
从操作上来看,没有叔叔的情况和叔叔为黑的情况是一样的.不过没有叔叔的情况是第一轮修正的状态,较为容易理解.
叔叔为黑色的情况下,黑结点数量不匹配,说明这种情况是上一次调整导致的(中间状态/不平衡状态);
没有叔叔的情况下,根据长度规则,此时已是最长路径(爷爷是最后一个非NIL黑结点),因此新增结点一定是最远结点,即插入后的第一次修正
- 左左(LL型):爷爷右单旋(降高度),交换父爷颜色

- 为什么要旋转?
在叔叔为空的情况下,插入红色结点可能会违反长度规则(一条路径中最长路径不超过最短路径的两倍),
(上图举例)
在上一篇AVL树中我们知道使用旋转子树可以降低高度(旋转过程在AVL树篇有详细描述,本篇不再具体描述,.同样的,红黑树在违反长度规则后也可以使用旋转来降低高度.经过验证,旋转处理可以有效解决违反长度规则问题.
如何旋转?
LL型中,对爷爷结点进行左旋,之后爷爷结点成为父结点的左孩子,高度-1;再交换父爷结点颜色,红黑树就平衡了.
旋转下来后为什么要变色? 如何变色?
旋转下来,父亲结点是祖先,是红色;但是爷爷是黑色,即以父结点为根的两条路径黑结点数量不平衡,一条多一个另一条少一个,这种情况下交换父爷结点颜色即可平衡.
- 左右(LR型):父左单旋(转成LL型),爷爷右单旋(降高度),交换父爷颜色.

3. 叔叔是黑色结点
(本身黑结点数量不匹配,说明这种情况一定是上一次调整导致的)
直接上图
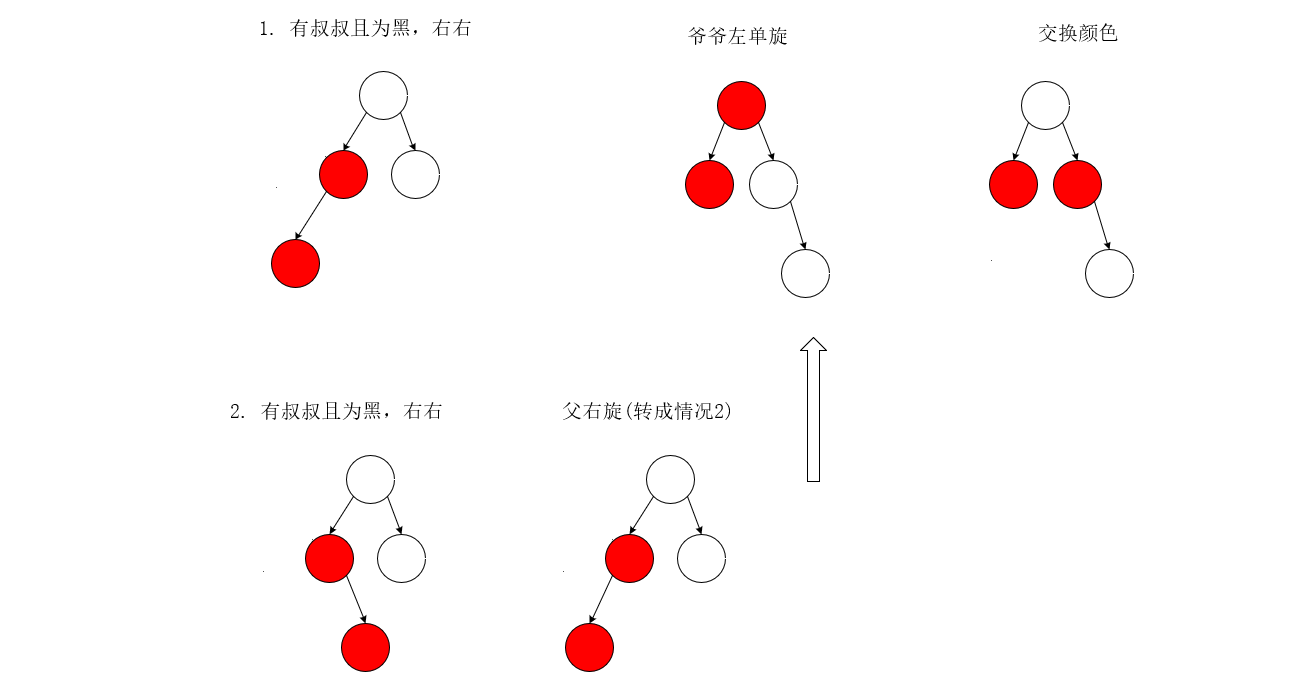
所有结构的基础衍生结构(以左为例)
在认识了简单结构后,我们对红黑树修正的基本情况有了大概的认识了.现在来分析这些结构怎么来的,下图是一个抽象结构,所有的需要修正的情况都是由下图所衍生.
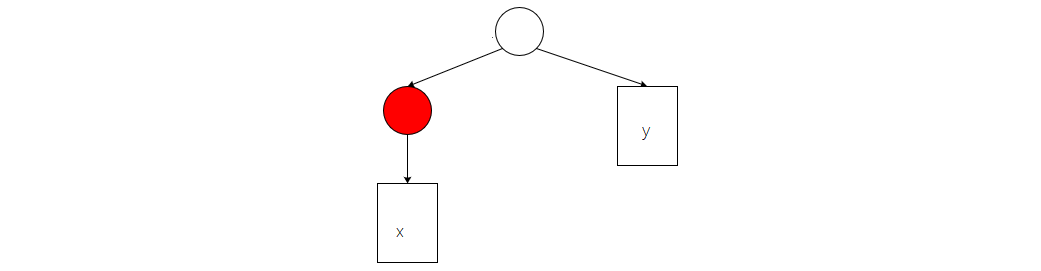
矩形▯为任意高度的子树,其中x为可能插入的位置,y是由x决定的(根据红黑树规则)。
简单情况衍生
当x为插入的结点时,

(△表示一个结点,其中a,b是新结点可能插入的位置,c只能为红色或没有结点。)
- 当c为一个红色结点时,衍生出以下情况

显然就是在上文的简单结构,红叔叔的情况.
- 当c为一个黑色结点时

和上文的一样,这种情况是修正中间状态,由上一轮修正引起的
- 当c为空时
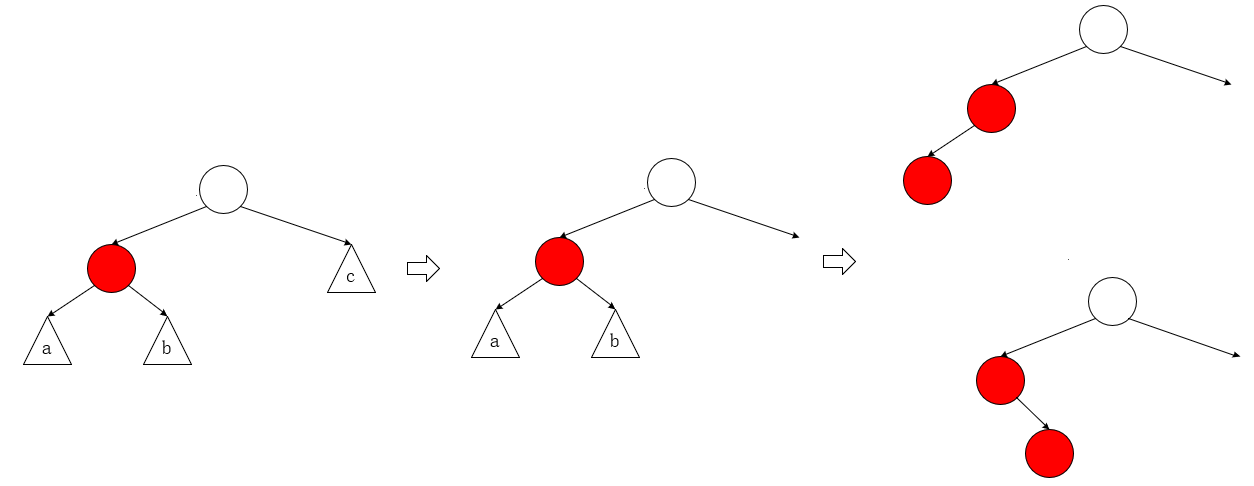
二级修正的情况衍生
当矩形x非插入结点,并根据
- 红黑树规则
- 和在简单情况中分析的,只有叔叔为红色结点时,才会使爷爷结点变红,进而可能影响到祖先结点
进行往下衍生一次,得到此图。
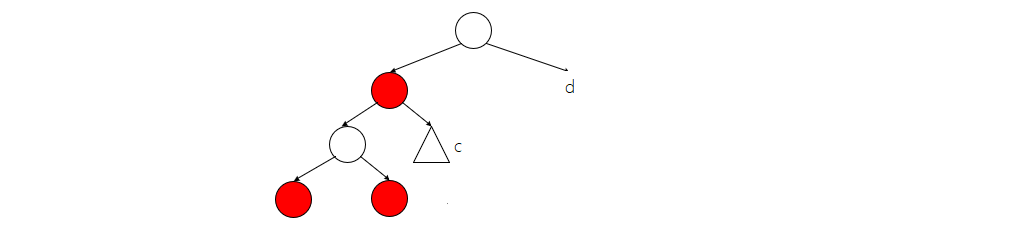
其中c为下图i/j/k/l中任意一种情况,d下面具体分析
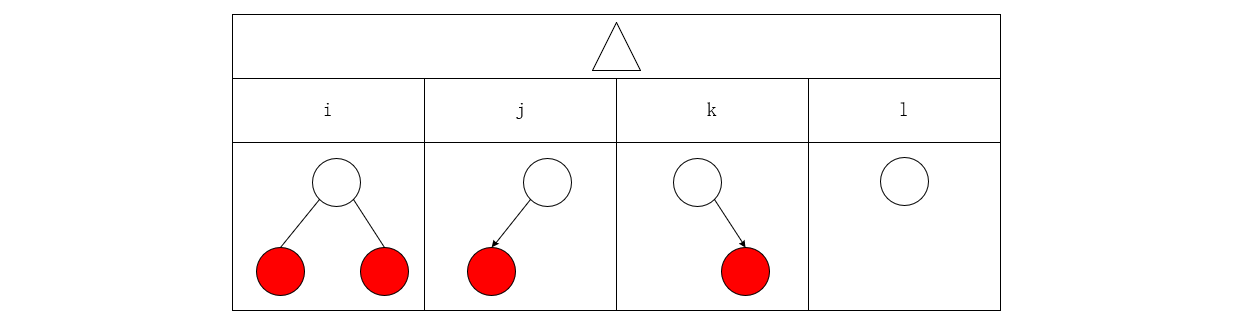
在最远结点四个位置插入均会引发爷爷结点变红。以插入最左位置为例
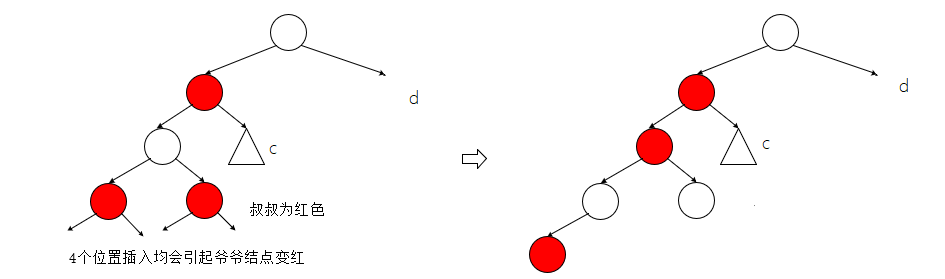
- d为红时

- d为黑时,有两种基本情况

其中a可能为i/j/k/l四种,b和c只能为空或者一个红色结点
- 当d为空时,在简单情况分析中得知调整方法和d为黑是一样的,可以复用,就不再分析了。
总结:
往后还有3级,4级...等,能够分析出都可以由1级推导出来,因此我们知道2级怎么来的就足够了,套用1级的方法,加上迭代修正,就能完成最终平衡.
完整代码实现
#include<iostream>
#include<chrono>
#include<functional>
#include<random>
#include<iomanip>
#include<string>
#include<cassert>
enum class Color { RED, BLACK };
template<class K, class V>
struct RBTreeNode {
//三叉链
RBTreeNode* _left;
RBTreeNode* _right;
RBTreeNode* _parent;
std::pair<K,V> _kv;
Color _col;
RBTreeNode(const decltype(_kv)& kv)
: _left(nullptr)
,_right(nullptr)
,_parent(nullptr)
,_kv(kv)
,_col(Color::RED) //默认为红,因为规则最宽松
{}
};
template<class K,class V>
class RBTree {
public:
using Node = RBTreeNode<K, V>;
RBTree()
:_root(nullptr)
{}
public:
Node* Find(const K& key) {
if (_root == nullptr) {
return false;
}
Node* cur = _root;
while (cur) {
if (key > cur->_kv.first) {
cur = cur->_right;
}
else if (key < cur->_kv.first) {
cur = cur->_left;
}
else {
return cur;
}
}
return nullptr;
}
bool Insert(const std::pair<K, V>& kv) {
if (_root == nullptr) {
_root = new Node(kv);
_root->_col = Color::BLACK;
return true;
}
Node* cur = _root;
Node* parent = _root;
while (cur) {
if (kv.first > cur->_kv.first) {
parent = cur;
cur = cur->_right;
}
else if (kv.first < cur->_kv.first) {
parent = cur;
cur = cur->_left;
}
else {
//存在相同的
return false;
}
} //while比较过程 [end]
//没找到,新增
cur = new Node(kv); //cur地址改变,只能使用kv进行比较(始终使用kv就好了)
//维护三叉链
cur->_parent = parent;
if (cur->_kv.first > parent->_kv.first) {
parent->_right = cur;
}
else {
parent->_left = cur;
}
//检查和调整红黑树
//FixInsert();
/**
* 右单旋情形 旋转后
* g(黑) | p(黑)
* p(红) u(黑) | c(红) g(红)
* c(红) | u(黑)
*/
/**
* 左右双旋情形 旋转后
* g(黑) | c(黑)
* p(红) u(黑) | p(红) g(红)
* x c(红) | x u(黑)
*/
while (parent && parent->_col == Color::RED) {
Node* grandpa = parent->_parent;
Node* uncle = nullptr;
if (parent == grandpa->_left && grandpa->_right) {
uncle = grandpa->_right;
}
else if (parent == grandpa->_right && grandpa->_left) {
uncle = grandpa->_left;
}
else {
uncle = nullptr;
}
//叔叔存在且为红
if (uncle && uncle->_col == Color::RED) {
parent->_col = Color::BLACK;
grandpa->_col = Color::RED;
uncle->_col = Color::BLACK;
cur = grandpa;
parent = grandpa->_parent;
}
//叔叔为黑色或无(已经确定左右父爷叔)
else {
//左左:对爷爷右单旋
if (cur == parent->_left && parent == grandpa->_left) {
RotateR(grandpa);
parent->_col = Color::BLACK;
grandpa->_col = Color::RED;
}
//左右:对父左单旋,对爷爷右单旋
else if (cur == parent->_right && parent == grandpa->_left) {
RotateL(parent); //转成左右,cur变成父,父变成子
RotateR(grandpa); //cur变成子树的根,右孩子是爷爷
cur->_col = Color::BLACK; //新爷爷变黑
grandpa->_col = Color::RED; //旧爷爷变红,和旧父同色
}
//右右
else if (cur == parent->_right && parent == grandpa->_right) {
RotateL(grandpa);
parent->_col = Color::BLACK;
grandpa->_col = Color::RED;
}
//右左
else if (cur == parent->_left && parent == grandpa->_right) {
RotateR(parent); //转成右右,此时cur变成父了
RotateL(grandpa); //cur变成子树的根,左孩子是爷爷
cur->_col = Color::BLACK; //新爷爷变黑
grandpa->_col = Color::RED; //旧爷爷变红,和旧父同色
}
//检查/排错
else {
assert(false);
}
//不需要更新变量,因为子树的根不是红了,不需要再更新
break;
}
}
//只有旋转会影响_root,旋转过程会自动更新_root,不用担心_root没有正确指向
//_root不影响所有路径的结点(同增同减),统一更新即可.
_root->_col = Color::BLACK;
return true;
}
void RotateL(Node* parent) {
Node* pparent = parent->_parent;
Node* cur = parent->_right;
Node* leftChild = cur->_left;
if (pparent) {
if (cur->_kv < pparent->_kv) {
pparent->_left = cur;
cur->_parent = pparent;
}
else {
pparent->_right = cur;
cur->_parent = pparent;
}
}
else {
cur->_parent = nullptr;
_root = cur;
}
parent->_right = leftChild;
if (leftChild) {
leftChild->_parent = parent;
}
cur->_left = parent;
parent->_parent = cur;
}
void RotateR(Node* parent) {
Node* pparent = parent->_parent;
Node* cur = parent->_left;
Node* rightChild = cur->_right;
//爷我
if (pparent) {
if (cur->_kv < pparent->_kv) {
pparent->_left = cur;
cur->_parent = pparent;
}
else {
pparent->_right = cur;
cur->_parent = pparent;
}
}
else {
cur->_parent = nullptr;
_root = cur;
}
//交换父子关系
cur->_right = parent;
parent->_parent = cur;
//托管
parent->_left = rightChild;
if (rightChild) {
rightChild->_parent = parent;
}
}
void InOrder() {
_InOrder(_root);
std::cout << std::endl;
}
bool IsBalance() {
//平衡条件
//1.根是黑
//2.红色结点不能连续
//3.所有路径黑色结点数量相同
// 实现方式:记录任意一条路径的黑结点数量,以该数量为基准,比较其他路径是否相等,不相等就是不平衡.(走到空就算是一条路径)
//条件1
if (_root == nullptr) return true;
if (_root->_col == Color::RED) return false;
//2和3需要遍历,因此另开一个函数
//2只需要结点即可,3还需要基准值和黑结点数量
int benchMark = 0;
Node* cur = _root;
while (cur) {
if (cur->_col == Color::BLACK) {
benchMark++;
}
cur = cur->_left;
}
return _check(_root, 0, benchMark);
}
bool _check(Node* root, int blackNum, const int benchMark) {
//条件3
if (root == nullptr) {
//走到根,路径结束,比较黑结点数量,只要有一个不同就是不同
//return blackNum == benchMark ? true : false;
if (blackNum != benchMark) {
std::cout << "基准值: " << benchMark << " 当前路径黑色结点数: " << blackNum << std::endl;
return false;
}
return true;
}
if (root->_col == Color::BLACK) {
blackNum++;
}
//条件2:相比于比较子(两步操作),比较父更简单(1步操作)
// 父结点一定存在:只有根不存在父结点,但根第一个就处理掉了
if (root->_col == Color::RED && root->_parent->_col == Color::RED) {
std::cout << "子结点: " << root->_kv.first << " 与父结点同为红色" << std::endl;
return false;
}
//通过条件:左右子树都为真
return _check(root->_left, blackNum, benchMark) && _check(root->_right, blackNum, benchMark);
}
int Hight() {
return _Hight(_root);
}
int _Hight(Node* root) {
if (root == nullptr) {
return 0;
}
int L = _Hight(root->_left);
int R = _Hight(root->_right);
return std::max(L, R) + 1;
}
~RBTree() {
Destroy(_root);
}
void Destroy(Node*& root) {
if (root == nullptr) {
return;
}
Destroy(root->_left);
Destroy(root->_right);
delete root;
}
private:
void _InOrder(Node* root) {
if (root == nullptr) {
return;
}
_InOrder(root->_left);
std::cout << root->_kv.first << " ";
_InOrder(root->_right);
}
private:
Node* _root;
};
BenchMark
与AVL树进行比较随机插入性能
测试环境:
| 架构: | x86_64 |
|---|---|
| CPU 运行模式: | 32-bit, 64-bit |
| CPU: | 16 |
| 在线 CPU 列表: | 0-15 |
| 型号名称: | AMD Ryzen 7 7840HS w/ Radeon 780M |
| CPU MHz: | 3792.879 |
| L1d 缓存: | 512 KiB |
| L1i 缓存: | 512 KiB |
| L2 缓存: | 16 MiB |
| L3 缓存: | 256 MiB |
| 系统: | Win10 |
| IDE: | VS2019 |
-
100万随机数(32位)


-
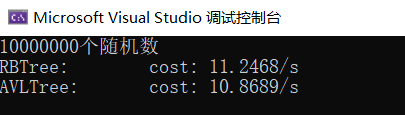
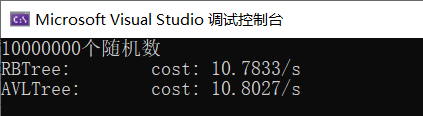
1000万随机数(32位)
-
一亿随机数(64位)
32位下1亿数据的红黑树/AVL树太大,大约3-6G左右,程序会奔溃.

测试发现随机数情况下红黑树的插入性能与AVL树差异不大.
红黑树的平衡要求不如AVL树严格,理论上search要慢些,实际也如此,不过差距并不大。虽然旋转次数少了,但由于红黑删除过程比较复杂,实际使用中性能差距也不算太大。
随机数+数据量小于1亿的情况下,两者差异不算太大.
测试源码
#include<iostream>
#include<chrono>
#include<functional>
#include<random>
#include<iomanip>
#include<string>
#include<cassert>
int* CopyArray(int* src, int size) {
assert(src && size);
int* tmp = new int[size];
memmove(tmp, src, size);
return tmp;
}
void Cost(std::function<void(void)> func) {
auto begin = std::chrono::high_resolution_clock::now();
func();
auto end = std::chrono::high_resolution_clock::now();
std::chrono::duration<double> cost = end - begin;
std::cout << cost.count() << "/s" << std::endl;
}
void RBInsertTest(RBTree<int, int>& t, int* a, int size) {
//test::RBTree<int,int> t;
for (int i = 0; i < size; i++) {
t.Insert(std::make_pair(a[i], a[i]));
//if (t.IsBalance() == false) assert(false);
}
}
void AVLInsertTest(AVLTree<int, int>& t,int* a, int size) {
for (int i = 0; i < size; i++) {
t.Insert(std::make_pair(a[i], a[i]));
//if (t.IsBalance() == false) assert(false);
}
}
void RandomArray_Generator(int* a, int n) {
std::random_device rnd;//random num device //效率低,只用于生成种子
std::mt19937 rng(rnd()); //random num generator -- 生成随机数
std::uniform_int_distribution<int> uni(0, 1000000000);//整型区间筛选
//[0-N]有6成为不重复,4成重复 --若需要9成不重复需要扩大筛选范围为10倍的N,即插入N需筛选10N
//int a[] = { 3,1,8,4,2,7,5,9,6,0 }; //自定义数组
int size = n;
std::cout << size << "个" << "随机数" << std::endl;
//std::cout<<size<<"个"<<"逆序数"<<std::endl;
//std::cout<<size<<"个"<<"正序数"<<std::endl;
//std::cout<<size<<"个"<<"重复数"<<std::endl;
for (int i = 0; i < size; i++) {
a[i] = uni(rng); //随机数
//a[i] = size - i; //逆序
//a[i] = i; //正序
//a[i] = size/2; //重复数
//if (i % 10000 == 0) {
// a[i] = uni(rng); //插入一些随机数
//}
}
}
void testInsert() {
//int a[] = { 16, 3, 7, 11, 9, 26, 18, 14, 15 };
//int a[] = { 4, 2, 6, 1, 3, 5, 15, 7, 16,14 };
//int size = sizeof(a)/sizeof(int);
int size = 10000000;
int* a = new int[size];
RandomArray_Generator(a, size);
std::cout << std::setw(15) << std::left;
std::cout << "RBTree: ";
RBTree<int,int> rbt;
Cost([&]() {std::cout << "cost: "; RBInsertTest(rbt, a, size); });
std::cout << std::setw(15) << std::left;
std::cout << "AVLTree: ";
AVLTree<int, int> avlt;
Cost([&]() {std::cout << "cost: "; AVLInsertTest(avlt, a, size); });
//Cost([&]() {std::cout << "cost: "; std::sort(a, a + size); });
}
void testHight() {
//int a[] = { 16, 3, 7, 11, 9, 26, 18, 14, 15 };
//int a[] = { 4, 2, 6, 1, 3, 5, 15, 7, 16,14 };
//int size = sizeof(a)/sizeof(int);
int size = 1000000;
int* a = new int[size];
RandomArray_Generator(a, size);
RBTree<int, int> rbt;
std::cout << std::setw(15) << std::left;
std::cout << "RBTree: "<<"\n";
RBInsertTest(rbt, a, size);
std::cout << "\t高度" << rbt.Hight()<<std::endl;;
AVLTree<int, int> avlt;
std::cout << std::setw(15) << std::left;
std::cout << "AVLTree: \n";
AVLInsertTest(avlt, a, size);
std::cout << "\t高度" << avlt.Hight()<<std::endl;
}
int main() {
//testInsert();
testHight();
}
本文来自博客园,作者:HJfjfK,原文链接:https://www.cnblogs.com/DSCL-ing/p/18377203




 浙公网安备 33010602011771号
浙公网安备 33010602011771号