随机化相关
随机函数
rand
生成伪随机数,头文件 #include<cstdlib> ,随机种子 srand(time(0))
返回一个 [0,RAND_MAX] 中的随机非负整数,其中 RAND_MAX 在 Linux 下等于 \(2^{31}-1\) ,在 Windows 下等于 \(2^{15}-1\)
注意 rand 的底层实现是 \(int\) 的,所以在 Linux 下不能左移!会爆 \(int\) 变成负数的!
在 Windows 下当需要生成的数不小于 \(2^{15}\) 时建议使用
(rand()<<15|rand())来生成更大的随机数
注意对于生成指定范围内的随机数,rand()%n 不保证均匀性,因为 [0,n) 中的每个数在 0\%n,1\%n,...,RAND\_MAX\%n 中出现的次数不一定相同
例:
srand(time(0));
int x=rand();
以下均为 C++11 标准下,头文件为 #include<random>
mt19937
随机数生成类,效果同 rand() ,范围同 unsigned int ,随机种子 mt19937 myrand(time(0))
相似的是 mt19937_64,使用方式同 mt19937,区别在于范围扩大到了 unsigned long long
例:
#include<ctime>
#include<random>
#define int long long
using namespace std;
signed main(){
mt19937 myrand(time(0));
int x=myrand();
printf("%lld\n",x);
}
minstd_rand0
线性同余算法
不会
random_shuffle
随机打乱指定序列,头文件 #include<algorithm>
区间左闭右开
内部随机数生成器默认 rand(),也可自定义。random_shuffle(first, last) 或 random_shuffle(first, last, myrand)
已于 C++14 标准中被弃用,于 C++17 标准中被移除
类似的有 shuffle,区别在于必须自定义随机数生成器即必须写 shuffle(first, last, myrand) 。random_shuffle 产生的排列不是等概率选的而 shuffle 是。
random_device
基于 Linux 内核熵池,依赖于熵池中收集的周围环境的噪声资源。这是真随机数,因为周围环境是不确定的,所以在熵池耗尽前可以生成高质量随机数,但是熵池耗尽后性能会急剧下降
常用于生成 mt19937 等伪随机数种子
注意:因为是基于 Linux 内核的,所以只在 Linux 下有效,在 Windows 下是不能用的。 在 Linux 下才会调用 dev/urandom 设备,而在 Windows 下调用的是 rand_s,效果等同于一般的伪随机数
例:
#include<iostream>
#include<ctime>
#include<random>
#define int long long
using namespace std;
int n;
signed main(){
mt19937 myrand(time(0));
// random_device rd;
// mt19937 gen(rd());//Linux
mt19937 gen(time(0));//Windows or Linux
uniform_int_distribution<> dis(1,10);
cin>>n;
for(int i=1;i<=n;i++) cout<<dis(gen)<<endl;
return 0;
}
随机数分布
要求随机数按照一定概率出现,以下是常见的随机分布模板类
| 类名 | 注释 |
|---|---|
uniform_int_distribution |
产生在一个范围上均匀分布的整数值 |
uniform_real_distribution |
产生在一个范围上均匀分布的实数值 |
bernoulli_distribution |
产生伯努利分布上的布尔值 |
binomial_distribution |
产生二项分布上的整数值 |
negative_binomial_distribution |
产生负二项分布上的整数值 |
geometric_distribution |
产生几何分布上的整数值 |
poisson_distribution |
产生泊松分布上的整数值 |
exponential_distribution |
产生指数分布上的实数值 |
gamma_distribution |
产生 \(\gamma\) 分布上的实数值 |
weibull_distribution |
产生威布尔分布上的实数值 |
extreme_value_distribution |
产生极值分布上的实数值 |
normal_distribution |
产生标准正态(高斯)分布上的实数值 |
lognormal_distribution |
产生对数正态分布上的实数值 |
chi_squared_distribution |
产生 \(x^2\) 分布上的实数值 |
cauchy_distribution |
产生柯西分布上的实数值 |
fisher_f_distribution |
产生费舍尔 F 分布上的实数值 |
student_t_distribution |
产生学生 t 分布上的实数值 |
discrete_distribution |
产生离散分布上的随机整数 |
piecewise_constant_distribution |
产生分布在常子区间上的实数值 |
piecewise_linear_distribution |
产生分布在定义的子区间上的实数值 |
例子和上面那个一样
注意:uniform_int_distribution 的随机数的范围不是半开范围 [ ),而是 [ ],对于 uniform_real_distribution 却是半开范围 [ )。
爬山算法(Hill Climbing)
是一个局部搜索算法,在规定的局部状态空间里进行搜索,得出局部最优解,用于多峰函数求最优值问题
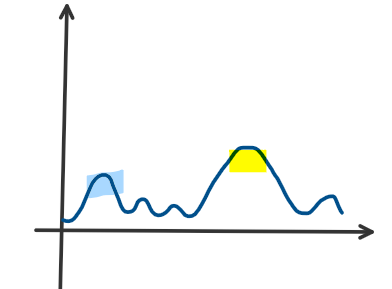
通俗地说,就是在当前最高山峰的相邻状态中找一个更高的山爬过去,如果找不到这样的山那就认为现在所在的山已经是最高的了,就说明当前的值就是最优解
但是事实上很容易找到一个局部最优解而不是全局最优解
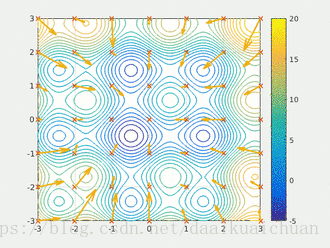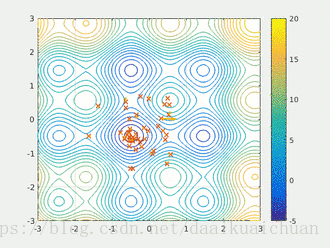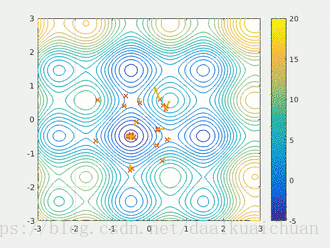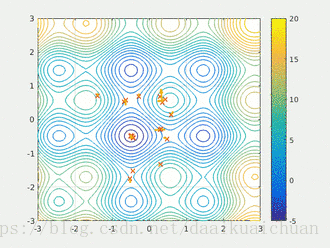
比如这样,你到了蓝色的山,以为自己是最优的了,但事实上黄色的山才是最优的
解决方法:多爬几次,规定个爬山的人数,给每个人 \(rand\) 出来一个初始位置让他从那开始爬,总答案取所有人里爬到的最大值,就大大增加了成功率
例题:
//头文件
#define N 1010
#define M 10000
#define ri register
using namespace std;
//快读
const double eps=1e-6;
const double delta=0.5;
double n,x[N],y[N],w[N],len=M,ansx,ansy;
inline void solve(double len){
double dx=0,dy=0;
for(ri int i=1;i<=n;i++){
double tmp=sqrt((x[i]-ansx)*(x[i]-ansx)+(y[i]-ansy)*(y[i]-ansy));
if(!tmp) continue;
dx+=w[i]/tmp*(x[i]-ansx);
dy+=w[i]/tmp*(y[i]-ansy);
}
double tmp=sqrt(dx*dx+dy*dy);
if(!tmp) return ;
ansx+=len/tmp*dx;
ansy+=len/tmp*dy;
}
int main(){
read(n);
for(ri int i=1;i<=n;i++) read(x[i]),read(y[i]),read(w[i]);
for(double len=M;len>eps;len*=delta) solve(len);
printf("%.3lf %.3lf\n",ansx,ansy);
return 0;
}
/*
3
0 0 1
0 2 1
1 1 1
//
0.577 1.000
*/
模拟退火(SA)
从爬山算法可以看出,直接把局部不优的解扔了挺傻的,为了跳出这个局部最优解去找全局最优解,我们有时候要接受局部不太优的解。这就是模拟退火
退火在百度百科上的解释是这样的:
退火是一种金属热处理工艺,指的是将金属缓慢加热到一定温度,保持足够时间,然后以适宜速度冷却
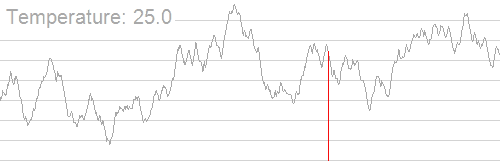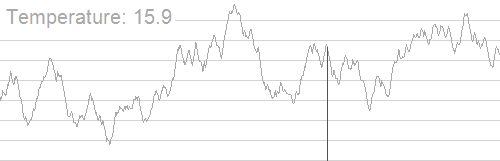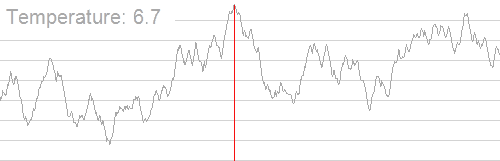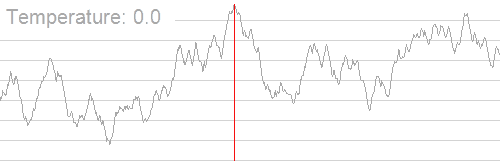
引用一张 OI Wiki 上的图能挺形象的说明这个过程:
算法就是如果搜到的新状态的解更优就更新答案,否则以一定概率接受这个新状态
设当前温度为 \(T\),新状态(从已知状态结合一定的随机化得到的)与已知状态之间的能量差为 \(\Delta E(\Delta E\ge 0)\),则发生状态转移的概率为
模拟退火的参数为:初始温度 \(T_0\)(一个比较大的数),降温系数 \(d\)(一个 \(0\sim 1\) 但是较为接近 \(1\) 的数,比如 \(0.95\) 这样的),终止温度 \(T_k\)(一个 \(0\sim 1\) 但是接近 \(0\) 的数,比如 \(0.001\) 这样的)
初始时 \(T=T_0\),每按着上面那个转移一次就降一点温,把 \(T\) 更新成 \(d\times T\),当温度降到 \(T<T_k\) 时就认为已经降到常温了,当前的解就是最优解
小技巧:
- 分块模拟退火:对于一个多多多多峰函数不好找最优解,给它按值域分块,每块跑一遍,取总的最优解
- 给程序记个时,一直跑模拟退火,直到快 \(T\) 了就退出:
while ((double)clock()/CLOCKS_PER_SEC < MAX_TIME)(其实对于挺多随机化应该都能这么搞)
例题:
P5544 [JSOI2016]炸弹攻击1 (事板子!)
在写了
粒子群优化算法(PSO)
属于群智能优化算法。模仿鸟类捕食的过程,先随机撒一堆点来模拟鸟群,鸟群在一起搜索整个区域中唯一的食物,每个鸟都知道自己离食物有多远且把信息与其他鸟共享。显然,最快找到食物的办法是搜索离食物最近的鸟附近的区域,于是所有鸟都逐渐向那附近靠拢
就像这样(图片来自网络)
初始化鸟的位置是随机的,每个鸟有速度和方向两个属性,速度代表移动的快慢,方向代表移动的方向。每个鸟在自己应该搜的范围内找到个体最优解,然后把这个消息和其他鸟分享,从里面找最优的作为当前全局最优解。其他鸟根据这个位置调整自己的速度和方向
设个体最优解为 \(pbest_i\),全局最优解为 \(gbest_i\),当前粒子速度为 \(v_i\),当前粒子位置为 \(x_i\),\(c_1,c_2\) 是学习因子,通常为 \(2\)(别问我我也不知道为啥),\(rand()\) 表示一个 \(0\sim 1\) 的随机数,惯性因子为 \(\omega\) ,其值为非负
有三个公式:
公式一:
其中第一项为记忆项,第二项为自身认知项,第三项为群体认知项
公式二:
公式三:
其中 \(\omega\) 是用来调整全局寻优能力和局部寻优能力的,改善了普通粒子群算法陷入局部最优的情况。\(\omega\) 越大全局寻优能力越强,局部寻优能力越弱。\(\omega\) 可以是固定值也可以动态改变,常用的动态改变惯性的方法为线性递减权值策略:
其中 \(G_k\) 为最大迭代次数,\(\omega_{ini}\) 为初始惯性权值,\(\omega_{end}\) 为迭代至最大进化代数时的惯性权值。典型权值为 \(\omega_{ini}=0.9,\omega_{end}=0.4\)
在以上三个公式中,公式一、二为 \(PSO\) 的标准形式公式,公式二、三为标准 \(PSO\) 算法
例题:
P2571 [SCOI2010]传送带 (看了首赞题解才知道这个算法的QAQ)
在写了
参考资料:


 浙公网安备 33010602011771号
浙公网安备 33010602011771号