2021.07.07笔记-数学2
写在前面
讲师:\(SGColin\)
内容:数论分块 欧拉函数求和 组合计数 概率 期望
2021.07.06笔记-数学1见wsy_jim's blog
数论分块
概念
将 \(1...n\) 按照 $\left \lfloor \frac{n}{i} \right \rfloor $ 的值进行划分
正确性:这里就不证了咕
复杂度:\(O(\sqrt n)\)
\(code:\)
for(int l=1,r,t;l<=n;l=r+1){
t=n/l;
// r=n/t;//在这个例子里不用取min也够用了
r=(n/l)?min(n,n/t):n;//一般都会给两个变量有可能超过n所以要取min
// cout<<l<<" "<<r<<endl;
ans+=(r-l+1)*t;//例子:求和
}
求值
-
其中 \(k\) 指分块的个数, \(t_k\) 指第 \(k\) 个块的值(下同)
-
\[\sum_{i=1}^{n}\left \lfloor \frac{n}{i} \right \rfloor=\sum_{k}(\frac{n}{l_k})\times (r_k-l_k+1) \]
-
\[\begin{aligned} &\sum_{i=1}^{n}n \% i \\ =&\sum_{i=1}^{n}(n-\left \lfloor \frac{n}{i} \right \rfloor \times i) \\ =&n^2-\sum_{k}t_k \sum_{i=l_k}^{r_k}i \\ \end{aligned} \]
其中的 \(\sum_{i=l_k}^{r_k}i=\frac{(l_k+r_k)(r_k-l_k+1)}{2}\) (等差数列求和公式)
-
\[\begin{aligned} &\sum_{i=1}^{n}\left \lfloor \frac{n}{i} \right \rfloor (n \% i) \\ =&\sum_{i=1}^{n}\left \lfloor \frac{n}{i} \right \rfloor(n-\left \lfloor \frac{n}{i} \right \rfloor \times i) \\ =&n\sum_{i=1}^{n}\left \lfloor \frac{n}{i} \right \rfloor -\sum_{k}t_k^2\sum_{i=l_k}^{r_k}i \\ \end{aligned} \]
应用
- 杜教筛(今天没学,以后学了再来填坑)
-
[CQOI2007]余数求和
其实和求值2是一样的
(因为变量名冲突所以这里用 \(k'\) 表示分块的个数)
\[\begin{aligned} &\sum_{i=1}^{n}k \% i \\ =&\sum_{i=1}^{n}(k-\left \lfloor \frac{k}{i} \right \rfloor \times i) \\ =&n\times k-\sum_{k'}t_{k'} \sum_{i=l_{k'}}^{r_{k'}}i \\ \end{aligned} \]\(code\)
signed main(){ read(n),read(k); ans=n*k; for(int l=1,r,t;l<=n;l=r+1){ t=k/l; r=(k/l)?min(n,k/t):n; // cout<<l<<" "<<r<<endl; ans-=(r-l+1)*((l+r)*t)/2;//注意 (l+r)*t的顺序!不然会爆零!因为下取整了! } cout<<ans<<endl; return 0; } -
膜膜塔
有题目没链接给定两个长度为 \(n\) 的数列 \(A,B\) ,求长度为 \(n\) 的数列 \(c\) ,\(n\le 10^5\)。
\[\begin{aligned} C_i &=\sum_{j=1}^i A_{\left \lfloor \frac{i}{j} \right \rfloor} B_{i \% j} \\ &=\sum_{j=1}^i A_{\left \lfloor \frac{i}{j} \right \rfloor} B_{i-\left \lfloor \frac{i}{j} \right \rfloor j} \\ &=\sum_k A_{t_k} \sum_{i=l_k}^{r_k}B_{i-t_k \times j} \\ \end{aligned} \]前一个求和号 \(O(\sqrt n)\) 求,后一个求和号 \(O(1)\) 求
显然正常来说是做不到 \(O(1)\) 的,所以我们要想其他办法
怎么能做到呢?
显然我们可以预处理(以下来自 \(Blueqwq\) )
在 \(B\) 的下标 \(i-t_k\times j\) 中,\(i\) 不变,\(j\) 随枚举的区间而变且每次只变 \(1\) ,所以 \(B\) 在区间 \([l_k,r_k]\) 中每次只会减少 \(t_k\) (\(t_k\) 的最大值只有 \(\sqrt n\) )
设 \(f_{i,j}\) 表示下标从 \(i\) 开始每次向前跳 \(j\) ,一直跳到下标为 \(i\mod j\) 的位置时 \(B\) 的前缀和(\(f_{i,j}\) 的大小为 \(n\sqrt n\) )
递推式:\(f_{i-j,j}=f_{i,j}+B_{i-j}\)
枚举 \(k\) 后计算 \(\sum_{i=l_k}^{r_k}B_{i-t_k \times j}\) 时,只需用 \(f_{i-t_k \times l_k}-f_{i-t_k(r_k+1)}\) 即可实现 \(O(1)\) 查询
总复杂度 \(O(n \sqrt n)\)
-
模积和
\(\sum_{i=1}^n\sum_{j=1}^m(n\%i)(m\%j) \ (i\not= j),n,m \le 10^9\)
\[\begin{aligned} 原式&=\sum_{i=1}^n \sum_{j=1}^m (n-\left \lfloor \frac{n}{i} \right \rfloor i)(m-\left \lfloor \frac{m}{j} \right \rfloor j) -\sum_{i=1}^{min(n,m)}(n\%i)(m\%i)\\ &=\sum_{i=1}^n \sum_{j=1}^m(nm+\left \lfloor \frac{n}{i} \right \rfloor \left \lfloor \frac{m}{j} \right \rfloor ij-n\left \lfloor \frac{m}{j} \right \rfloor j-m\left \lfloor \frac{n}{i} \right \rfloor i) -\sum_{i=1}^{min(n,m)}(n\%i)(m\%i) \\ &=\sum_{i=1}^n(n-\left \lfloor \frac{n}{i} \right \rfloor i)\sum_{j=1}^m(m-\left \lfloor \frac{m}{j} \right \rfloor j)-\sum_{i=1}^{min(n,m)}(nm+\left \lfloor \frac{n}{i} \right \rfloor \left \lfloor \frac{m}{i} \right \rfloor i^2-(m\left \lfloor \frac{n}{i} \right \rfloor+n\left \lfloor \frac{m}{i} \right \rfloor)i) \\ \end{aligned} \]
欧拉函数求和
-
前置知识
欧拉函数:小于\(x\) 的整数中与 \(x\) 互质的数的个数,一般用 \(\varphi(x)\) 表示。特殊的, \(\varphi(1)=1\)
计算欧拉函数通式:
\[\varphi(x)=x\prod_{i=1}^{n} (1-\frac{1}{p_i}) \ (\varphi(1)=1) \]其中 \(p_1,p_2,...p_n\) 为 \(x\) 的所有质因数,\(x\) 是正整数
-
[SDOI2008]仪仗队
\(\sum_{i=1}^n\sum_{j-1}^n[(i,j)=1],n\le 10^4\)
\[\begin{cases} & ans(1)=0 \\ & ans(n)=2\sum_{i=0}^{n-1}\varphi (i)+1,n>1 \end{cases} \] -
[BZOJ2818]GCD
\(\sum_{i=1}^n\sum_{j=1}^n[(i,j)is \ prime],n\le10^7\)
\[\begin{aligned} 原式&=\sum_p\sum_{i=1}^n\sum_{j=1}^n[(i,j)=p] \\ &=\sum_p\sum_{i=1}^{\left \lfloor \frac{n}{p} \right \rfloor }\sum_{j=1}^{\left \lfloor \frac{n}{p} \right \rfloor } [(i,j)=1] \\ &=\sum_p (2 \sum_{i=1}^{\left\lfloor\frac{n}{p}\right\rfloor}\varphi(i)-1) \end{aligned} \]然后用线性筛求欧拉函数前缀和即可
-
P2398
\(\sum_{i =1}^n\sum_{j =1}^n(i,j),n\le 10^5\)
\[\begin{aligned} 原式&=\sum_dd\sum_{i=1}^n\sum_{j=1}^n[(i,j)=d] \\ &=\sum_d(2d\sum_{i=1}^{\left \lfloor \frac{n}{d} \right \rfloor }\varphi(i)-1) \end{aligned} \] -
上一道题的加强版
这题8倍经验的说UVA11426 拿行李(极限版) GCD - Extreme (II)
SP19985 GCDEX2 - GCD Extreme (hard)
\(\sum_{i=1}^n\sum_{j=1}^{i-1}(i,j),n\le 10^6\) ,多组询问
\[\begin{aligned} g(i)&=\sum_{j=1}^{i-1}\sum_{j=1}^{i-1}(i,j) \\ &=\sum_{d|i}\sum_{j=1}^{i-1}[(\frac{i}{d},\frac{j}{d})=1] \\ &=\sum_{d|i}\varphi(\left \lfloor \frac{i}{d} \right \rfloor ) \end{aligned} \]伪代码:
for(int d=1;d<=n;++d){ for(int i=d;i<=n;i+=d){ g(i)+=phi(i/d); } }复杂度为调和级数:\(\sum_{1\le i \le n}\frac{n}{i}=O(\log n)\)
-
签到题
设 \(f(x)\) 表示 \([1,x]\) 内与 \(x\) 不互质的数的个数,求 \(\sum_{i=1}^rf(i)\% p\) ,\(r-l\le 10^6\) ,\(l,r \le 10^{12}\)
\[f(x)=x-\varphi(x) \\ \varphi(x)=x\prod_{i=1}^{m}\frac{p_i-1}{p_i} \]对于每个数,考虑质因数分解,我们只需求出这个数有哪些质因子,然后暴力求 \(\varphi\) 即可
\(10^{12}\) 当然是过不去的,事实上我们只筛 \(10^6\) 内的所有质数即可,从而得到 \(\sqrt n\) 以内的质因子。对于 \([10^6,10^{12}]\) 的数 \(x\) ,我们用刚才求的那些质因子一直除它,直到不能再整除为止。此时剩下的 \(>1\) 的数即为 \(>\sqrt x\) 的质因子,然后求 \(\varphi\) 即可
伪代码:
for(int j=1;j<=tot;j++){ for(int i=(l/p[j])*p[j];i<=(r/p[j])*p[j];i+=p[j]){ phi[i]*=((p[j]-1)/p[j]); } } -
骗分过样例
区间筛法
因为这题太毒瘤了所以跑去翻题解,结论大概是面向测试点编程并不在课件范围之内,不搞了不搞了qwq
-
[SPOJ5971]LCM
\(\sum_{i=1}^n[i,n],n\le 10^6\) , 多组询问 , \(T\le 3\times 10^5\)
还是和之前一样推推推推推式子,过程就不放了这里放个化简结果吧
数学题的大部分意义不都在推式子的过程吗\[\sum_{i=1}^nlcm(i,n)=n\sum_{d|n}\sum_{i=1}^di[gcd(i,d)==1]=n\sum_{d|n}\frac{\varphi(d)d}{2} \]
组合计数
四大基本原理
- 加法原理
- 乘法原理
- 减法原理(补集转化)
- 除法原理(同构)(多用于群论中)
例题
-
不相交路径计数
补集转化,所有路径对数(拓扑排序)-相交路径对数
本题题解来自@wsy_jim
给定\(n\)个点的 DAG ,计数有序对\(a\rightarrow b,c\rightarrow d\)的数目
• 满足路径\(a\rightarrow b,c\rightarrow d\)没有公共点
• n ≤ 200, m ≤ 20000
给出的图是DAG,我们可以通过拓扑排序在DAG上维护很多参量,这道题让求不相交的路径对数,我们可以记录下两个值,一个是f[i][j],表示从i到j共有多少条路径,另一个是g[i],表示有多少个点对(a,b)满足路径\(a\rightarrow i\)和\(b\rightarrow i\)无交点
利用乘法原理以及容斥原理可以推出DP式子:
\[g[i]=f[a][i]*f[b][i]-\sum_{拓扑序在i之前的点j}g[j]*(f[j][i])^2 \]最后的答案就是
\[ans=f[a][b]*f[c][d]-\sum g[j]*f[j][b]*f[j][d] \]
排列与组合
- 排列
- 圆排列
- 组合数
- 通项公式和递推公式是组合数的两种基本求解方法,应根据数据范围选定方法
-
全错位排列
使得对于任何 \(i\in [1,n]\) ,满足第 \(i\) 个位置上的数不是 \(i\) 的排列数
\[D_1=0,D_2=1 \]\[D_n=(n-1)(D_{n-1}+D_{n-2}) \] -
二项式定理
\[(x+a)^n=\sum_{k=0}^{k}C_n^kx^ka^{n-k} \]- 试证明 \(\sum_{k=0}^nC_n^k=2^n\)
- 性质:
\[\sum_{i=0}^n(-1)^iC_n^i=0(奇数位的和=偶数位的和)\\ C_n^mC_m^r=C_n^rC_{n-r}^{m-r}\\ 递推公式:C_n^m=C_{n-1}^m+C_{n-1}^{m-1}(总=n不选+n选)\\ \]
例题
-
组合数问题
就是板子,用杨辉三角预处理可过
Lucas定理
扩展Lucas定理
统计分子分母里 \(p\) 出现的次数,然后用分子里的个数减去分母里的个数,如果 \(>0\) 那么 \(\%p\) 的结果为 \(0\) ( \(p\) 是组合数的因子)
例题
-
礼物
-
[ARC117C]砖块
- 由真值表推式子(本质就是打表找规律)
卡特兰数
卡特兰数是组合数学中一个常出现在各类计数问题中的数列
数列的前几项为:\(1, 2, 5, 14, 42, 132, 429, 1430, 4862, 16796, 58786, 208012, 742900, 2674440, 9694845,...\)
证明:
该证明也就是卡特兰数最常用的一个变形:
卡特兰数也有递推式:
- 计数问题 \(or\) \(DP\)
- 锻炼敏感度,看见出现了几项上述那些数就要考虑卡特兰数,看不出来可打表
-
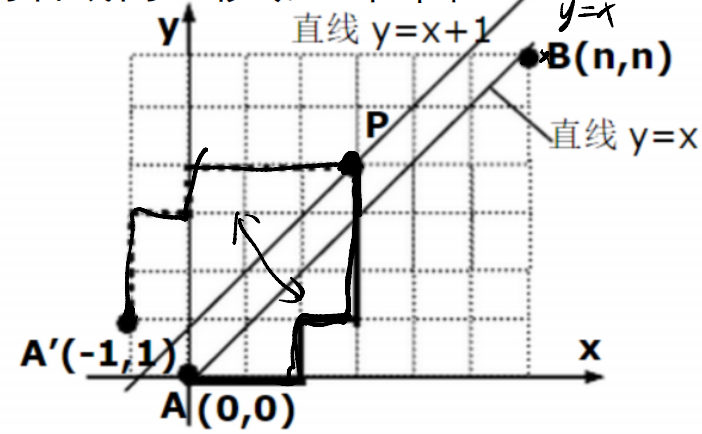
折线/括号序列/01串
就是从不同角度对卡特兰数的理解
放一张课件上的图:
-
\(n\) 个点二叉树划分
求 \(n\) 个节点能构成几种不同的二叉树
假设现在为中序遍历,根节点第 \(k\) 个被访问到,则根节点的左子树有 \(k-1\) 个节点,右子树有 \(n-k\) 个节点,\(1 \le k \le n\) ,容易发现这样的计算方法正好和卡特兰数的递推式一致,或者说递推式可又这种方法得到
-
\(n+3\) 个点凸多边形三角剖分
(图片来自网络)
 \[H_n=\sum_{k=3}^{n-1}H_kH_{n-k+2} \]
\[H_n=\sum_{k=3}^{n-1}H_kH_{n-k+2} \]
例题
路径
斐波那契数列
-
性质
- \(f_1+f_2+f_3+...+f_n=f_{n+2}-1\)
- \(f_1^2+f_2^2+f_3^2+...+f_n^2=f_n f_{n+1}\)
- \(f_1+f_3+f_5+...+f_{2n-1}=f_{2n}\)
- \(f_2+f_4+f_6+...+f_{2n}=f_{2n+1}-1\)
- \(f_n=f_mf_{n-m-1}+f_{m-1}f_{n-m}(n \ge m)\)
- \(f_{n-1}f_{n+1}=f_n^2+(-1)^n\)
-
应用
- 递推公式加速计算
- 模质数循环节
-
斐波那契和 \(gcd\) 关系
- \(gcd(fib(i),fib(j))=fib(gcd(i,j))\)
- \(n|m \Leftrightarrow fib(n)|fib(m)\)
八类基本计数问题
- 有无标号
- 排列/组合
- 是否重复
- 球同盒不同,不可空:\(C_{n-1}^{m-1}\)
- 球同盒不同,可空:\(C=_{n+m-1}^{m-1}\)
- 球不同盒同,不可空:(第二类斯特林数)$f[i][j]=j*f[i-1][j]+f[i-1][j-1] $
- 球不同盒同,可空:\(\sum_{i=1}^{m}S[n][i]\)
- 球不同盒不同,不可空: \(S[n][m]*m!\)
- 球不同盒不同,可空:\(m^n\)
- 球同盒同,不可空:\(f[n][m]=f[n-1][m-1]+f[n-m][m]\)
- 球同盒同,可空:球少:\(f[i][j]=f[i][i]\) 球多:\(f[i][j]=f[i-1][j]+f[i][j-1]\)
斯特林数
第一类斯特林数
将 \(n\) 个数划分为 \(m\) 个圆排列的方案数
第二类斯特林数
将 \(n\) 个数划分为 \(m\) 个集合的方案数
例题
楼房
按照最高点分为左右两部分,左边能看到 \(f\) 栋,右边能看到 \(b\) 求出第一类斯特林数 \(S_{n-1,f-1+b-1}\) ,即把除最高楼之外的楼排成 \(f-1+b-1\) 个圈。分好组后,直接从 \(f+b-2\) 个组中选出 \(f-1\) 组放左边,共有 \(C_{f+b-2}^{f-1}\) 种选择。
由乘法原理可得,共有 \(S_{n-1,f-1+b-1} \times C_{f+b-2}^{f-1}\) 种方案数
注意,当 \(n-1<f+b-2\) 时无解,输出 \(0\)
概率 期望
古典概型
离散的
几何概型
连续的
加法原理&乘法原理
独立事件:
并列事件:
条件概率
当事件 \(j\) 已经发生时,事件 \(i\) 发生的概率:
-
当太阳已经从东边升起 \(n\) 次后,求第 \(n+1\) 次从东边升起的概率
\[P(n)=\frac{n+1}{n+2} \] -
三门问题
有三道题 \(A,B,C\) ,分别为两个水题和一个神题,已经随便选了一道题,又已知另外两个里面的某一个是水题,现想要切到神题,问应不应该用手里的这道换剩下的那道?
答:应该。不换能赢的概率是 \(\frac{1}{3}\) ,换了能赢的概率是 \(\frac{2}{3}\)
证明见这里
-
扩展三门问题
[UVA10491] 奶牛和轿车 Cows and Cars
\(A\) 个水题,\(B\) 个神题,做完决策后告诉你 \(C\) 个水题的情况,求换/不换时切到神题的概率 \((C<A)\)
\[神题\left\{\begin{matrix} 水题\to \frac{A}{A+B}·\frac{B}{A+B-C-1} \\ 神题 \to \frac{B}{A+B}·\frac{B-1}{A+B-C-1} \end{matrix}\right. \]因为上面这两种情况为并列事件,所以把它们相加就是答案
\[ans=\frac{AB+B^2-B}{(A+B)(A+B-C-1)} \]
期望
线性性质
设 \(x_i\) 表示事件 \(i\) 的权重
则可以得到
例题
-
骗分
-
Kids and Prizes
-
进场
-
翻牌
-
DEBUG
①顺推:4种状态, \(O(n^2) \ DP\) ②逆推:4种状态倒过来
-
增长
-
摇奖
均摊复杂度 \(O(1)\)
-
粒子加速器
-
石头剪刀布
-
期望树
(JZOJ):①线段树维护区间或(暴力改,不用打标记) ②线段树询问区间和 ③期望,拆开算,补式子(区间和的平方!)
-
猫和老鼠
- 稀疏图(点边同一级别的,此时可认为入队次数不会超过10)用SPFA不会被卡,但是相差超过10倍就最好别用
- 逆推 不是直接从终态找到初态 是在搜索过程中记忆化搜索找到终态
- 记搜+SPFA
-
期望的例题共11道,实在写不动了qwq,改天再补吧
不咕不咕不咕!!!


