大数据技术与应用课堂测试 -神经网络计算过程
石家庄铁道大学2024年春季
2021 级大数据技术与应用课堂测试
-神经网络计算过程
课程名称： 大数据技术与应用 任课教师： 王建民
1、用自己的话说明深度学习训练三部群正向传播，反向传播，梯度下降的基本功能和原理。
（1）正向传播是输入数据通过神经网络，从输入层流向输出层的过程。在正向传播中，这一层的神经元接收上一层的输出，再进行加权求和、计算激活函数，然后将结果传给下一层。这个过程一直持续到达输出层，产生网络的预测结果。
（2）反向传播是通过计算损失函数对网络参数的梯度来调整参数，使得网络的预测结果更加接近真实标签。首先，通过比较网络预测值和真实标签计算出损失函数的值。然后，反向传播算法利用链式法则从输出层向输入层传播梯度，计算损失函数对每个参数的梯度。最后，利用这些梯度信息更新网络参数，以减小损失函数的值。
（3）梯度下降是一种优化算法，用于最小化损失函数。在深度学习中，通常使用反向传播计算损失函数对参数的梯度。然后，根据梯度的反方向，以一定的步长（学习率）更新参数，使得损失函数逐渐减小。这个过程一直持续迭代，直到达到预定的停止条件，如达到最大迭代次数或损失函数收敛到某个阈值。
2、请问人工神经网络中为什么ReLu要好过于tanh和sigmoid function？
（1）ReLU的计算速度更快，因为它只涉及简单的阈值比较和取最大值的操作。相比之下，sigmoid和tanh函数需要进行指数运算，这在计算上更为复杂，特别是在处理大型深度网络时，ReLU可以节省大量的计算资源。
（2）sigmoid和tanh函数在输入值过大或过小时，其导数会变得非常接近0，这会导致反向传播中的梯度消失问题。梯度消失意味着在深层网络中，通过多个sigmoid或tanh层传播梯度时，梯度会逐渐变得非常小，导致网络训练变得非常缓慢，甚至无法收敛。而ReLU在正数部分保持导数为1，这有助于解决梯度消失问题，使网络训练更加高效。
（3）ReLU的一个关键特性是它可以使网络具有稀疏性。在ReLU中，负数部分被截断为0，所以在每个神经元上只有一部分激活。这种稀疏性有助于减少神经网络的过拟合风险，因为每个神经元都在处理少量信息，从而降低了模型的复杂度。此外，这种分段线性性质使得网络能够逐渐构建复杂的非线性表示能力。综上所述，ReLU因其计算效率、对梯度消失问题的缓解以及稀疏激活性等特点，在人工神经网络中通常比tanh和sigmoid函数更具优势。然而，不同的激活函数在不同的应用场景中可能有不同的表现，因此在实际应用中需要根据具体任务和网络结构来选择合适的激活函数。
3、为什么引入非线性激励函数？
（1）神经网络的堆叠层如果只包含线性变换，整个网络仍然只能实现线性变换，无法学习复杂的非线性关系。通过引入非线性激活函数，可以使网络能够学习和表示更复杂的非线性关系，提高网络的表达能力。
（2）在深层神经网络中，如果只使用线性激活函数，梯度会随着网络的深度逐渐消失，导致训练困难。非线性激活函数可以通过保持梯度不至于过小，有助于缓解梯度消失问题，使得深层网络更容易训练。
（3）非线性激活函数可以引入更多的非线性特征，使得神经网络可以更好地适应复杂的输入数据分布，提高了网络的表达能力和泛化能力。
（4）非线性激活函数可以帮助网络更快地收敛到合适的解，提高了网络的稳定性和训练速度。
4、根据样例：
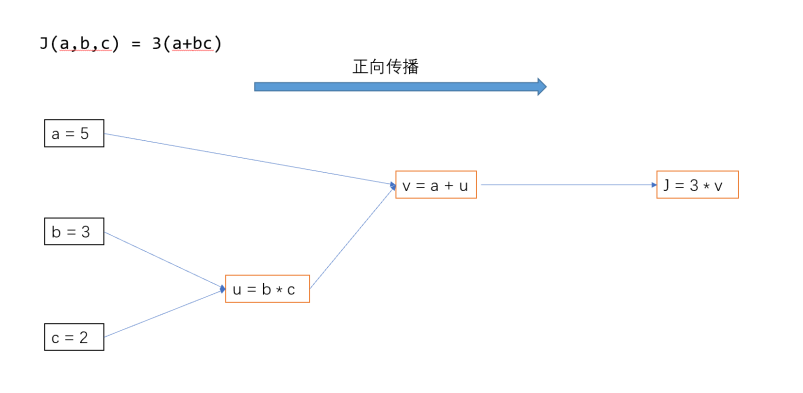
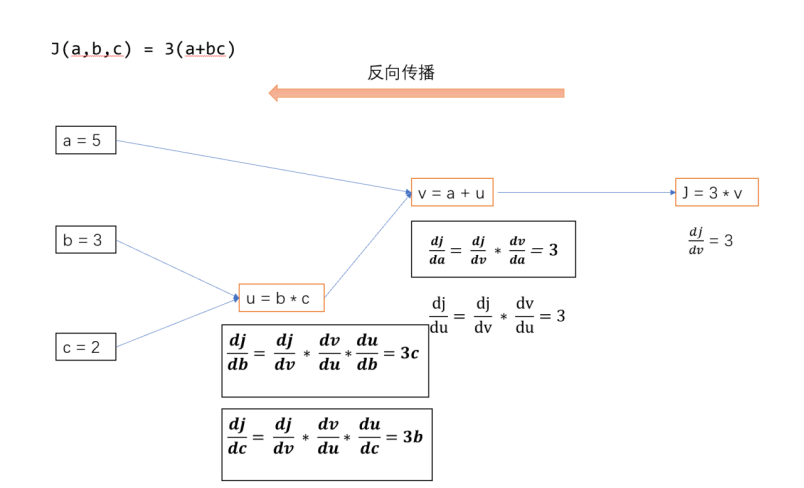
计算出模型正向传播、反向传播的各个神经元的输入与输出。模型中的非线性函数采用Relu，方向传播的损失函数结果为Y。
其中 X1 =1，X2 = -1，要求计算Z_1, Z_2, Z_3，并写出计算过程。
Z_1 = X1*(W_1)+X2*(W_2) = 1*1-1*2= -1
Z_2 = X1*(W_3)+X2*(W_4) = -1*1-1*1 = -2
a_1=1/(1+e^(-Z_1))=1/(1+e^1)=0.2689
a_2=1/(1+e^(-Z_2))=1/(1+e^2)=0.1192
Z_3=(W_5)*(a_1) +(W_6)*(a_2)=0.3881
y=1/(1+e^(-Z_3))=1/(1+e^(-0.3881))=0.5958
