HIAST Collegiate Programming Contest 2024（非完全题解）

C题（简单数据结构+二分）

转化成对每个i，求最长区间使得区间与为ai。左右边界可以二分出来（类似24新生赛B），区间与用st表

// #pragma GCC optimize("O3,unroll-loops")
// #pragma GCC target("avx2,bmi,bmi2,lzcnt,popcnt")
// //如果在不支持 avx2 的平台上将 avx2 换成 avx 或 SSE 之一
#include<bits/stdc++.h>
using namespace std;
#define x first
#define y second
typedef pair<int,int> PII;
typedef long long ll;
typedef unsigned long long ull;
typedef unsigned int uint;
typedef vector<string> VS;
typedef vector<int> VI;
typedef vector<vector<int>> VVI;
vector<int> vx;
inline void divide() {sort(vx.begin(),vx.end());vx.erase(unique(vx.begin(),vx.end()),vx.end());}
// inline int mp(int x) {return upper_bound(vx.begin(),vx.end(),x)-vx.begin();}
inline int log_2(int x) {return 31-__builtin_clz(x);}
inline int popcount(int x) {return __builtin_popcount(x);}
inline int lowbit(int x) {return x&-x;}
inline ll Lsqrt(ll x) { ll L = 1,R = 2e9;while(L + 1 < R){ll M = (L+R)/2;if(M*M <= x) L = M;else R = M;}return L;}
#define N 100005
int f[25][N];
int Log2[N];
int n,a[N];
int query(int l,int r)
{
    int k = Log2[r-l+1];
    return f[k][l] & f[k][r-(1<<k)+1];
}

void solve()
{
    cin>>n;
    for(int i=1;i<=n;++i) cin>>a[i], f[0][i]=a[i];
    for(int j=1;j<=Log2[n];++j)
    {
        for(int i=1;i+(1<<j-1)<=n;++i)
        {
            f[j][i] = (f[j-1][i] & f[j-1][i+(1<<j-1)]);
        }
    }

    for(int i=1;i<=n;++i)
    {
        int l,r,mid;
        int L,R;
        l=1; r=i;
        while(l<r)
        {
            mid = (l+r)>>1;
            if(query(mid, i) == a[i]) r=mid;
            else l=mid+1;
        }
        L=l;
        l=i, r=n;
        while(l<r)
        {
            mid = (l+r+1)>>1;
            if(query(i, mid) == a[i]) l=mid;
            else r=mid-1;
        }
        R=l;
        cout<<(ll)(R-i+1)*(i-L+1)<<' ';
    }
    cout<<'\n';
}
int main()
{
	ios::sync_with_stdio(false);
	cin.tie(0);
    Log2[0]=-1;
    for(int i=1;i<N;++i) Log2[i] = Log2[i/2]+1;
	int T;
	cin>>T;
	while(T--)
	{
		solve();
	}
}

H（博弈）

\(关注到不管是移动一个还是三个都会改变sum的奇偶性\)

    // #pragma GCC optimize("O3,unroll-loops")
    // #pragma GCC target("avx2,bmi,bmi2,lzcnt,popcnt")
    // //如果在不支持 avx2 的平台上将 avx2 换成 avx 或 SSE 之一
    #include<bits/stdc++.h>
    using namespace std;
    #define x first
    #define y second
    typedef pair<int,int> PII;
    typedef long long ll;
    typedef unsigned long long ull;
    typedef unsigned int uint;
    typedef vector<string> VS;
    typedef vector<int> VI;
    typedef vector<vector<int>> VVI;
    vector<int> vx;
    inline void divide() {sort(vx.begin(),vx.end());vx.erase(unique(vx.begin(),vx.end()),vx.end());}
    inline int mp(int x) {return upper_bound(vx.begin(),vx.end(),x)-vx.begin();}
    inline int log_2(int x) {return 31-__builtin_clz(x);}
    inline int popcount(int x) {return __builtin_popcount(x);}
    inline int lowbit(int x) {return x&-x;}
    inline ll Lsqrt(ll x) { ll L = 1,R = 2e9;while(L + 1 < R){ll M = (L+R)/2;if(M*M <= x) L = M;else R = M;}return L;}
    void solve()
    {
        int n;
        cin>>n;
        int a;
        ll sum = 0;
        for(int i=0;i<n;++i)
        {
            cin>>a;
            sum += a;
        }
        cout<<((sum&1)?("YES\n"):("NO\n"));
    }
    int main()
    {
        ios::sync_with_stdio(false);
        cin.tie(0);
        int T;
        cin>>T;
        while(T--)
        {
            solve();
        }
    }

I（纯签到）

\(注意find函数若没找到是!=npos没有括号\)

// #pragma GCC optimize("O3,unroll-loops")
// #pragma GCC target("avx2,bmi,bmi2,lzcnt,popcnt")
//如果在不支持 avx2 的平台上将 avx2 换成 avx 或 SSE 之一
#include<bits/stdc++.h>
using namespace std;
#define x first
#define y second
typedef pair<int,int> PII;
typedef long long ll;
typedef unsigned long long ull;
typedef unsigned int uint;
typedef vector<string> VS;
typedef vector<int> VI;
typedef vector<vector<int>> VVI;
vector<int> vx;
inline void divide() {sort(vx.begin(),vx.end());vx.erase(unique(vx.begin(),vx.end()),vx.end());}
// inline int mp(int x) {return upper_bound(vx.begin(),vx.end(),x)-vx.begin();}
inline int log_2(int x) {return 31-__builtin_clz(x);}
inline int popcount(int x) {return __builtin_popcount(x);}
inline int lowbit(int x) {return x&-x;}
inline ll Lsqrt(ll x) { ll L = 1,R = 2e9;while(L + 1 < R){ll M = (L+R)/2;if(M*M <= x) L = M;else R = M;}return L;}
void solve()
{
    string s;
    cin>>s;
    string std = "bitset";
    if(s.find(std) != s.npos)
    {
        cout<<"7as\n";
    }
    else
    {
        cout<<"no 7as for you today\n";
    }
}
int main()
{
	ios::sync_with_stdio(false);
	cin.tie(0);
	int T;
	cin>>T;
	while(T--)
	{
		solve();
	}
}

K题（LCA，dfs序，思维）

倒水问题，可以发现对一个子树，从根开始倒水，结点进水顺序为dfs序。
对每个询问，从v开始倒水要想去u，必定经过lca(u,v)，过程可以分为两部分，从v到r和从r到u，分类讨论求代价即可。

// #pragma GCC optimize("O3,unroll-loops")
// #pragma GCC target("avx2,bmi,bmi2,lzcnt,popcnt")
//如果在不支持 avx2 的平台上将 avx2 换成 avx 或 SSE 之一
#include<bits/stdc++.h>
using namespace std;
#define x first
#define y second
typedef pair<int,int> PII;
typedef long long ll;
typedef unsigned long long ull;
typedef unsigned int uint;
typedef vector<string> VS;
typedef vector<int> VI;
typedef vector<vector<int>> VVI;
vector<int> vx;
inline void divide() {sort(vx.begin(),vx.end());vx.erase(unique(vx.begin(),vx.end()),vx.end());}
inline int mp(int x) {return upper_bound(vx.begin(),vx.end(),x)-vx.begin();}
inline int log_2(int x) {return 31-__builtin_clz(x);}
inline int popcount(int x) {return __builtin_popcount(x);}
inline int lowbit(int x) {return x&-x;}
inline ll Lsqrt(ll x) { ll L = 1,R = 2e9;while(L + 1 < R){ll M = (L+R)/2;if(M*M <= x) L = M;else R = M;}return L;}

#define N 100005
int n,q;
vector<int> e[N];
vector<int> edfn[N];
int fa[N], siz[N], dep[N], son[N], top[N];
int dfn[N];
int tot;
void dfs_init(int u)
{
    siz[u] = 1;
    son[u] = 0;
    dfn[u] = ++tot;
    for(auto &&v:e[u])
    {
        dep[v] = dep[u] + 1;
        dfs_init(v); 
        siz[u] += siz[v];
        if(siz[v] > siz[son[u]]) son[u] = v;
    }

    edfn[u].resize(e[u].size());
    for(int i=0;i<e[u].size();++i)
    {
        edfn[u][i] = dfn[e[u][i]];
    }
}
void dfs_shupou(int u,int topx)
{
    top[u] = topx;
    if(son[u]) dfs_shupou(son[u], topx);
    for(auto &&v:e[u])
    {
        if(v==son[u]) continue;
        dfs_shupou(v, v);
    }
}
int lca(int x,int y)
{
    while(top[x] != top[y])
    {
        if(dep[top[x]] < dep[top[y]]) swap(x,y);
        x = fa[top[x]];
    }
    if(dep[x] < dep[y]) return x;
    else return y;
}

void solve()
{
    cin>>n>>q;
    tot = 0;
    for(int i=1;i<=n;++i) e[i].clear(), edfn[i].clear();
    for(int i=2;i<=n;++i)
    {
        cin>>fa[i];
        e[fa[i]].push_back(i);
    }
    for(int i=1;i<=n;++i) sort(e[i].begin(),e[i].end());
    dep[1]=0;
    dfs_init(1);
    dfs_shupou(1,1);

    while(q--)
    {
        int v,x,u; cin>>v>>x>>u;
        auto f = [&](int y){cout<<(x>=y?"YES\n":"NO\n");};
        if(u==v) {f(1); continue;}
        
        int r = lca(v,u);
        // int fu = e[r][upper_bound(edfn[r].begin(), edfn[r].end(), dfn[u])-1-edfn[r].begin()];
        if(dfn[u] < dfn[v])
        {
            int fv = e[r][upper_bound(edfn[r].begin(), edfn[r].end(), dfn[v])-1-edfn[r].begin()];
            f(dfn[u]-dfn[r]+1 + siz[fv]);
        }
        else
        {
            f(dfn[u]-dfn[r]+1);
        }
    }
}
int main()
{
	ios::sync_with_stdio(false);
	cin.tie(0);
	int T;
	cin>>T;
	while(T--)
	{
		solve();
	}
}

H题（简单构造）

\(当x为10次幂时显然无解，否则为离他最近的10次幂\)

// #pragma GCC optimize("O3,unroll-loops")
// #pragma GCC target("avx2,bmi,bmi2,lzcnt,popcnt")
//如果在不支持 avx2 的平台上将 avx2 换成 avx 或 SSE 之一
#include<bits/stdc++.h>
using namespace std;
#define x first
#define y second
typedef pair<int,int> PII;
typedef long long ll;
typedef unsigned long long ull;
typedef unsigned int uint;
typedef vector<string> VS;
typedef vector<int> VI;
typedef vector<vector<int>> VVI;
vector<int> vx;
inline void divide() {sort(vx.begin(),vx.end());vx.erase(unique(vx.begin(),vx.end()),vx.end());}
inline int mp(int x) {return upper_bound(vx.begin(),vx.end(),x)-vx.begin();}
inline int log_2(int x) {return 31-__builtin_clz(x);}
inline int popcount(int x) {return __builtin_popcount(x);}
inline int lowbit(int x) {return x&-x;}
inline ll Lsqrt(ll x) { ll L = 1,R = 2e9;while(L + 1 < R){ll M = (L+R)/2;if(M*M <= x) L = M;else R = M;}return L;}
set<ll> P;
void solve()
{
    ll x;
    cin>>x;
    ll inf = 1e18;
    if(P.find(x)!=P.end()) cout<<"-1\n";
    else 
    {
        auto it = P.lower_bound(x);
        cout<<*it<<'\n';
    }
}
int main()
{
	ios::sync_with_stdio(false);
	cin.tie(0);
    ll tmp = 1;
    P.insert(1);
    for(int i=1;i<=18;++i) {tmp = 10*tmp;P.insert(tmp);}
	int T;
	cin>>T;
	while(T--)
	{
		solve();
	}
}

D（数学）

\(原先两个式子经过简单推导后（真的很简单）可变成 x^3 =a_i^2a_j , y^3 =a_j^2a_i ,我们考虑x,y,a_i,a_j质因数分解，假设对于某个质数p，四个数分解出的质数分别x_p,y_p,\)
\((a_i)_p,(a_j)_p,那么有3*x_p = 2*(a_i)_p+(a_j)_p和3*y_p = 1*(a_i)_p+2*(a_j)_p。注意到等式左边mod3 = 0 所以解这个式子最后得到（a_i)_p = (a_j)_p(mod3),也\)
\(就是说有价值的i，j对他们质因数分解后得到的次幂在mod3意义下每个数字相等，那么我们对于每个输入的x = p ^ 3*s,用x除去最大的这个数可以看作x的质因数分解后在mod3下的的唯一合法表示\)

#include<bits/stdc++.h>
using namespace std;
#define x first
#define y second
typedef pair<int,int> PII;
typedef long long ll;
typedef unsigned long long ull;
typedef unsigned int uint;
typedef vector<string> VS;
typedef vector<int> VI;
typedef vector<vector<int>> VVI;
vector<int> vx;
inline void divide() {sort(vx.begin(),vx.end());vx.erase(unique(vx.begin(),vx.end()),vx.end());}
// inline int mp(int x) {return upper_bound(vx.begin(),vx.end(),x)-vx.begin();}
inline int log_2(int x) {return 31-__builtin_clz(x);}
inline int popcount(int x) {return __builtin_popcount(x);}
inline int lowbit(int x) {return x&-x;}
inline ll Lsqrt(ll x) { ll L = 1,R = 2e9;while(L + 1 < R){ll M = (L+R)/2;if(M*M <= x) L = M;else R = M;}return L;}

#define N 50005
int n, x;
unordered_map<int,int> mp;
void solve()
{
    cin>>n;
    mp.clear();
    ll ans = 0;
    for(int i=1;i<=n;++i)
    {
        cin>>x;
        int p = pow(x,1.0/3);
        p ++;
        for( ;p ; --p)
        {
            int p3 = p*p*p;
            if(x % p3) continue;
            ans += mp[x / p3];
            ++mp[x / p3];
            break;
        }
    }
    cout<<ans<<'\n';

}
int main()
{
	ios::sync_with_stdio(false);
	cin.tie(0);
	int T;
	cin>>T;
	while(T--)
	{
		solve();
	}
}

J（找规律）

\(显然考虑重合边当且仅当为中线，否则对于与X轴垂直坐标为x来说寻找Y轴坐标为x或A-x（排除四等分），或者是X轴为2\times x，A-x，Y轴同理\)

// #pragma GCC optimize("O3,unroll-loops")
// #pragma GCC target("avx2,bmi,bmi2,lzcnt,popcnt")
//如果在不支持 avx2 的平台上将 avx2 换成 avx 或 SSE 之一
#include<bits/stdc++.h>
using namespace std;
#define x first
#define y second
typedef pair<int,int> PII;
typedef long long ll;
typedef unsigned long long ull;
typedef unsigned int uint;
typedef vector<string> VS;
typedef vector<int> VI;
typedef vector<vector<int>> VVI;
vector<int> vx;
inline void divide() {sort(vx.begin(),vx.end());vx.erase(unique(vx.begin(),vx.end()),vx.end());}
inline int mp(int x) {return upper_bound(vx.begin(),vx.end(),x)-vx.begin();}
inline int log_2(int x) {return 31-__builtin_clz(x);}
inline int popcount(int x) {return __builtin_popcount(x);}
inline int lowbit(int x) {return x&-x;}
inline ll Lsqrt(ll x) { ll L = 1,R = 2e9;while(L + 1 < R){ll M = (L+R)/2;if(M*M <= x) L = M;else R = M;}return L;}

int n;
map<int,int> mpx,mpy;

void solve()
{
    cin>>n;
    int xs,ys,xe,ye;
    cin>>xs>>ys>>xe>>ye;
    int A = xe-xs;
    bool ok=false;
    for(int i=1;i<=n;++i)
    {
        int x1,y1,x2,y2;
        cin>>x1>>y1>>x2>>y2;
        x1-=xs; y1-=ys;
        x2-=xs; y2-=ys;
        if(x1==x2) 
        {
            if(x1*2==A && mpx.find(x1) != mpx.end()) 
            {
                cout<<mpx[x1]<<' '<<i<<'\n';
                ok = true;
                break; 
            }
            mpx[x1]=i;
        }
        else if(y1==y2) 
        {
            if(y1*2==A && mpy.find(y1) != mpy.end()) 
            {
                cout<<mpy[y1]<<' '<<i<<'\n';
                ok = true;
                break; 
            }
            mpy[y1]=i;
        }
    }
    if(ok) return;
    for(auto &&[x,i]:mpx)
    {
        if(2*x == A) continue;
        if(mpy.find(x) != mpy.end()) {cout<<i<<' '<<mpy[x]<<'\n'; return;}
        if(mpy.find(A-x) != mpy.end()) {cout<<i<<' '<<mpy[A-x]<<'\n'; return;}
        if(mpx.find(2*x) != mpx.end() && 3*x != A) {cout<<i<<' '<<mpx[2*x]<<'\n'; return;}
        if(mpx.find(A-x) != mpx.end() && 3*x != A) {cout<<i<<' '<<mpx[A-x]<<'\n'; return;}
    }
    for(auto &&[y,i]:mpy)
    {
        if(2*y == A) continue;
        if(mpy.find(2*y) != mpy.end() && 3*y != A) {cout<<i<<' '<<mpy[2*y]<<'\n'; return;}
        if(mpy.find(A-y) != mpy.end() && 3*y != A) {cout<<i<<' '<<mpy[A-y]<<'\n'; return;}
    }
    cout<<"-1 -1\n";
}
int main()
{
	ios::sync_with_stdio(false);
	cin.tie(0);
	int T=1;
	// cin>>T;
	while(T--)
	{
		solve();
	}
}

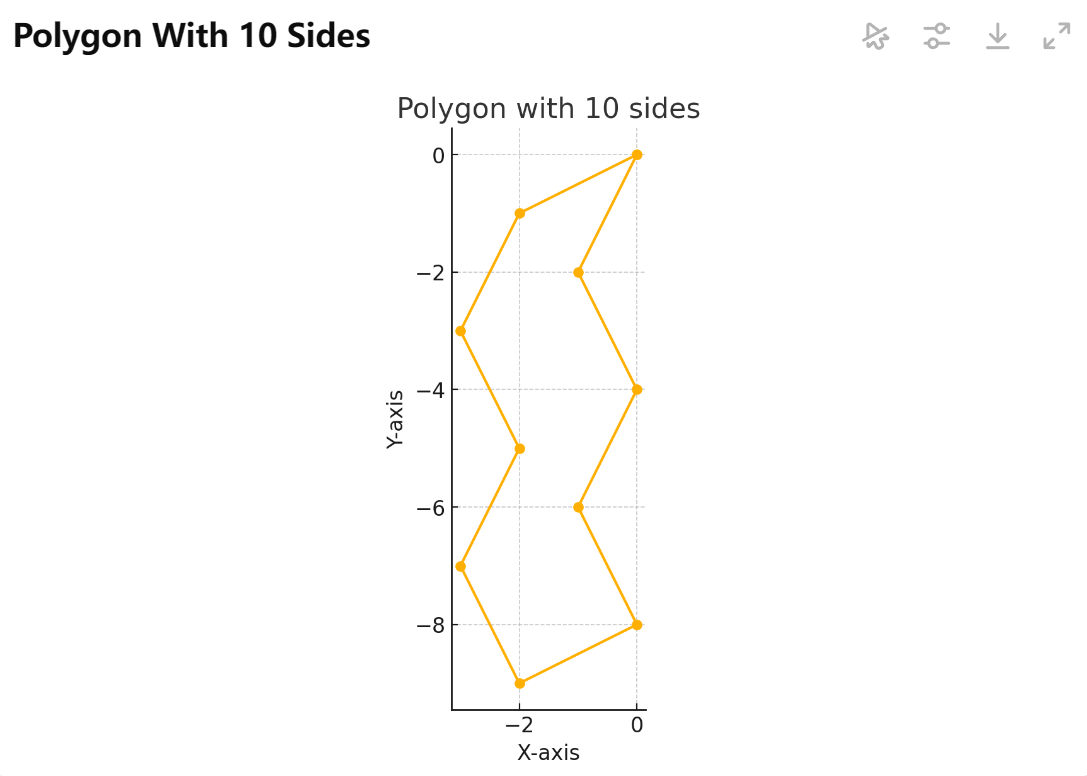
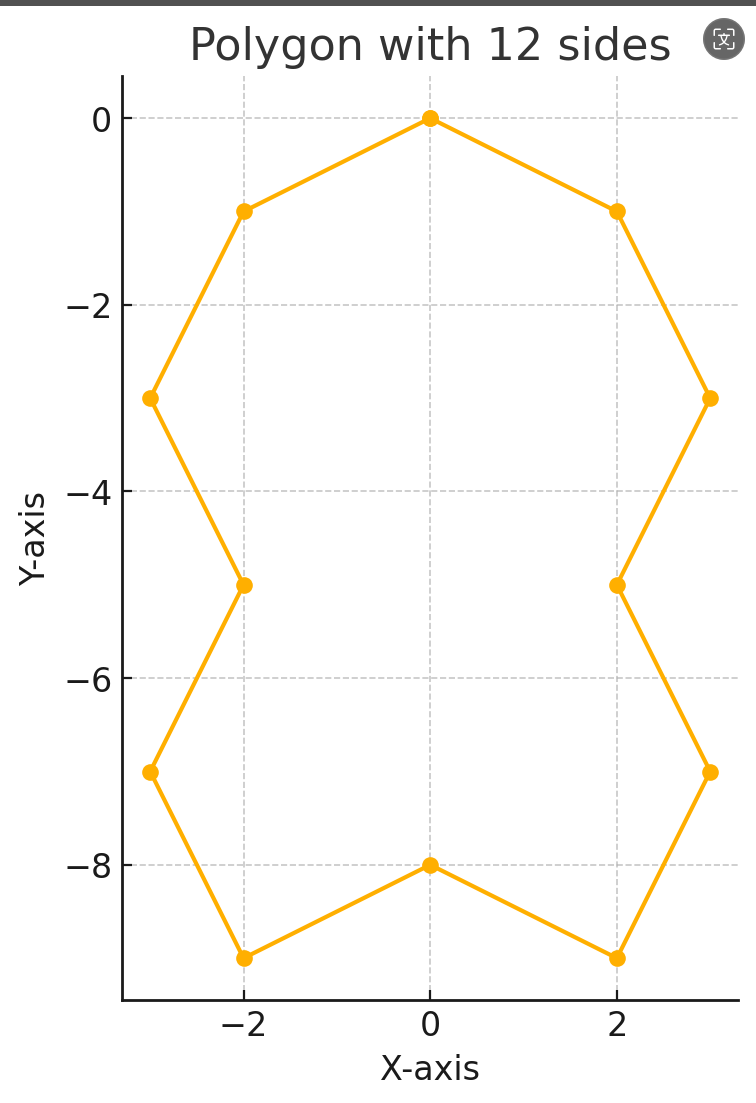
L（不好想的构造）

\(奇数没有，偶数可以，直接贴图，借鉴自O_start\)

class Node:
    def __init__(self, x, y):
        self.x = x
        self.y = y

def solve():
    t = int(input())  # 读取测试用例的数量
    for _ in range(t):
        n = int(input())  # 读取每个测试用例的多边形顶点数
        
        # 如果 n 是奇数，直接输出 -1
        if n % 2 != 0:
            print("-1")
        else:
            # 如果 n == 4，直接输出正方形的坐标
            if n == 4:
                print(f"0 0")
                print(f"0 1")
                print(f"1 1")
                print(f"1 0")
            else:
                # 如果 n 是 4 的倍数
                if n % 4 == 0:
                    tmp = Node(0, 0)
                    print(f"{tmp.x} {tmp.y}")
                    tmp.x += 2
                    tmp.y -= 1
                    print(f"{tmp.x} {tmp.y}")
                    for i in range(2, n // 2):
                        if i % 2 != 0:
                            tmp.x += 1
                            tmp.y -= 2
                        else:
                            tmp.x -= 1
                            tmp.y -= 2
                        print(f"{tmp.x} {tmp.y}")
                    
                    tmp.x -= 2
                    tmp.y += 1
                    print(f"{tmp.x} {tmp.y}")
                    
                    tmp.x -= 2
                    tmp.y -= 1
                    print(f"{tmp.x} {tmp.y}")
                    
                    for i in range(2, n // 2):
                        if i % 2 != 0:
                            tmp.x += 1
                            tmp.y += 2
                        else:
                            tmp.x -= 1
                            tmp.y += 2
                        print(f"{tmp.x} {tmp.y}")
                # 如果 n 不是 4 的倍数但仍为偶数
                else:
                    tmp = Node(0, 0)
                    print(f"{tmp.x} {tmp.y}")
                    for i in range(1, n // 2):
                        if i % 2 != 0:
                            tmp.x -= 1
                            tmp.y -= 2
                        else:
                            tmp.x += 1
                            tmp.y -= 2
                        print(f"{tmp.x} {tmp.y}")
                    
                    tmp.x -= 2
                    tmp.y -= 1
                    print(f"{tmp.x} {tmp.y}")
                    
                    for i in range(1, n // 2):
                        if i % 2 != 0:
                            tmp.x -= 1
                            tmp.y += 2
                        else:
                            tmp.x += 1
                            tmp.y += 2
                        print(f"{tmp.x} {tmp.y}")

# 调用解决函数
solve()