吴恩达深度学习笔记（八） —— ResNets残差网络

（很好的博客：残差网络ResNet笔记）

 

主要内容：

一.深层神经网络的优点和缺陷

二.残差网络的引入

三.残差网络的可行性

四.identity block 和 convolutional block

 

 

一.深层神经网络的优点和缺陷

1.深度神经网络很大的一个优点就是能够表示一个复杂的功能。网络的层数越多，意味着能够提取到不同level的特征越丰富。并且，越深的网络提取的特征越抽象，越具有语义信息。但其有一个巨大的缺陷，那就是：如果简单地增加深度，会导致梯度弥散或梯度爆炸。使得训练速度十分缓慢：

2.对于上述问题，解决方法是引入batch normalization，但这又会导致另一个问题，那就是“退化问题”。表现为网络层数增加，但是在训练集上的准确率却饱和甚至下降了。退化问题可能是因为深层的网络并不是那么好训练。

 

 

二.残差网络的引入

1.残差网络解决了增加深度带来的副作用（退化问题），这样就能够实现通过增加网络深度，来提高网络性能。

2.其基本思想是：在理想化的深层神经网络中，如果后面的网络层是恒等映射，那么深层神经网络就退化为浅层神经网络。所谓恒等映射就是输入等于输出（F(x) = x)，放在神经网络当中，那就是把前面的值，直接穿过若干个网络层（而没有经过任何实际性的处理），最后到达输出层。但是，深层神经网络在实际中并不那么理想，因为深层的网络并不是那么好训练，特别是学习恒等映射（至于为什么这样，我也是人云亦云）。

3.但是，深层的网络学习F(x) = 0，则相对容易（此也人云亦云，可能在后面的网络层，权重衰减严重，因而引入了batch normalization）。让深层神经网络学习F(x) = 0的方法是构建：H(x) = F(x) + x，对应于神经网络的结构图如下：

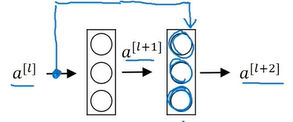
对于第l+2层，其总输出就是g(H(x))，也就是a[l+2]，而a[l+2] = g(a[l] + z[l+1])，又因为H(x) = F(x) + x，规定z[l+1]对应F(x)，a[l]对应x。因此，就是要学习z = 0，这对于深层的网络来说是没那么难的。

 

 

三.残差网络的可行性

为何学习深层的网络学习 z = 0 会可行呢？还是看会l+2层的表达式：

 

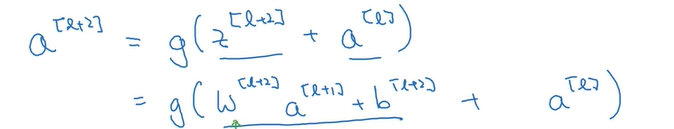
在深层的网络层，权重衰减严重，原因是引入了batch normalization，导致了w[l+2]、b[l+2]都接近于0，因此z[l+2]就接近于0，证明了残差网络是可行的。

 

 

四.identity block 和 convolutional block

1.残差网络，从感性上去认识，就是将当前的输出输入到下一层的同时，还增加一条路径输入到更后面的某一层。这样构成的一个块，叫做残差块，残差块就是构成残差网络的基础。

2.一般地，是将a[l]输入到第l+k层的激活函数之前（发明者通过实验证明的高效做法），即将a[l]和z[l+k]相加，然后送到激活函数中去。a[l]能和z[l+k]相加的前提条件是：a[l]的shape等于z[l+k]的shape。当两者相等时，可以直接输入进去，此种块称为identity block；当两者不同时，则需要将a[l]通过一个卷积层以调整其shape与z[l+k]一致，此种块称为convolutional block。