吴恩达深度学习笔记(三)—— 初始化
主要内容:
一.初始化问题
二.全0初始化
三.随机初始化
四.“He initialization”初始化
一.初始化问题
1.在深度学习中,参数的初始化对模型有着重要的影响,而需要初始化的参数有两类:
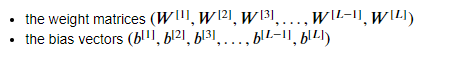
参数b的初始化对模型的影响较小,所以一般都是直接初始化为0,所以下面讨论的都是对参数W的初始化。 有三种不同的初始化方式:

以下代码是深度学习模型,需要传一个初始化方式的参数:

def model(X, Y, learning_rate = 0.01, num_iterations = 15000, print_cost = True, initialization = "he"): """ Implements a three-layer neural network: LINEAR->RELU->LINEAR->RELU->LINEAR->SIGMOID. Arguments: X -- input data, of shape (2, number of examples) Y -- true "label" vector (containing 0 for red dots; 1 for blue dots), of shape (1, number of examples) learning_rate -- learning rate for gradient descent num_iterations -- number of iterations to run gradient descent print_cost -- if True, print the cost every 1000 iterations initialization -- flag to choose which initialization to use ("zeros","random" or "he") Returns: parameters -- parameters learnt by the model """ grads = {} costs = [] # to keep track of the loss m = X.shape[1] # number of examples layers_dims = [X.shape[0], 10, 5, 1] # Initialize parameters dictionary. if initialization == "zeros": parameters = initialize_parameters_zeros(layers_dims) elif initialization == "random": parameters = initialize_parameters_random(layers_dims) elif initialization == "he": parameters = initialize_parameters_he(layers_dims) # Loop (gradient descent) for i in range(0, num_iterations): # Forward propagation: LINEAR -> RELU -> LINEAR -> RELU -> LINEAR -> SIGMOID. a3, cache = forward_propagation(X, parameters) # Loss cost = compute_loss(a3, Y) # Backward propagation. grads = backward_propagation(X, Y, cache) # Update parameters. parameters = update_parameters(parameters, grads, learning_rate) # Print the loss every 1000 iterations if print_cost and i % 1000 == 0: print("Cost after iteration {}: {}".format(i, cost)) costs.append(cost) # plot the loss plt.plot(costs) plt.ylabel('cost') plt.xlabel('iterations (per hundreds)') plt.title("Learning rate =" + str(learning_rate)) plt.show() return parameters
二.全0初始化
代码实现:

# GRADED FUNCTION: initialize_parameters_zeros def initialize_parameters_zeros(layers_dims): """ Arguments: layer_dims -- python array (list) containing the size of each layer. Returns: parameters -- python dictionary containing your parameters "W1", "b1", ..., "WL", "bL": W1 -- weight matrix of shape (layers_dims[1], layers_dims[0]) b1 -- bias vector of shape (layers_dims[1], 1) ... WL -- weight matrix of shape (layers_dims[L], layers_dims[L-1]) bL -- bias vector of shape (layers_dims[L], 1) """ parameters = {} L = len(layers_dims) # number of layers in the network for l in range(1, L): ### START CODE HERE ### (≈ 2 lines of code) parameters['W' + str(l)] = np.zeros((layers_dims[l],layers_dims[l-1])) parameters['b' + str(l)] = np.zeros((layers_dims[l],1)) ### END CODE HERE ### return parameters
测试结果:
parameters = model(train_X, train_Y, initialization = "zeros") print ("On the train set:") predictions_train = predict(train_X, train_Y, parameters) print ("On the test set:") predictions_test = predict(test_X, test_Y, parameters)


可以看出神经网络的作用完全失效了,退化成了随机决策,原因是:

三.随机初始化
随机初始化参数的具体步骤是:先采用np.random.randn()为参数分配呈高斯分布的随机数,然后再乘上一个数如10,以调整参数的规模。

# GRADED FUNCTION: initialize_parameters_random def initialize_parameters_random(layers_dims): """ Arguments: layer_dims -- python array (list) containing the size of each layer. Returns: parameters -- python dictionary containing your parameters "W1", "b1", ..., "WL", "bL": W1 -- weight matrix of shape (layers_dims[1], layers_dims[0]) b1 -- bias vector of shape (layers_dims[1], 1) ... WL -- weight matrix of shape (layers_dims[L], layers_dims[L-1]) bL -- bias vector of shape (layers_dims[L], 1) """ # np.random.seed(3) # This seed makes sure your "random" numbers will be the as ours parameters = {} L = len(layers_dims) # integer representing the number of layers for l in range(1, L): ### START CODE HERE ### (≈ 2 lines of code) parameters['W' + str(l)] = np.random.randn(layers_dims[l],layers_dims[l-1]) * 10 parameters['b' + str(l)] = np.zeros((layers_dims[l],1)) ### END CODE HERE ### return parameters
测试效果:
parameters = model(train_X, train_Y, initialization = "random") print ("On the train set:") predictions_train = predict(train_X, train_Y, parameters) print ("On the test set:") predictions_test = predict(test_X, test_Y, parameters)

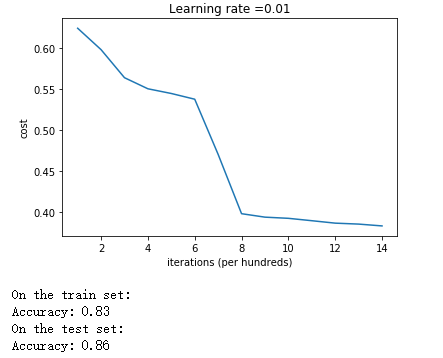
1.从准确率可以看出,随机初始化的效果比较理想。但是细看时,发现刚刚初始化完没有开始迭代时,代价函数为inf无穷大。为什么呢?
因为在初始化时我们还乘上了一个参数10,这个数在sigmoid函数里面比较大了,这也导致参数W的绝对值比较大,使得Z = WX + b的绝对值比较大,从而sigmod(Z)无限接近于0或1。当分类错误时,根据logistic回归的损失函数的图像可知,此时的损失无限大。


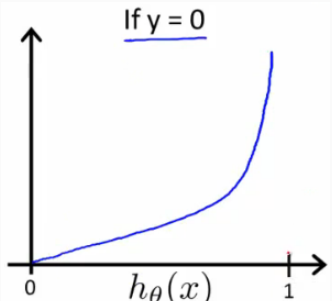
2.不好的初始化可能导致梯度消失或者梯度爆炸,而以较大规模的值去初始化参数可能会延长取得最优参数的过程。所以总得来说,用较小规模的值去初始化参数可以胜任这份工作,但怎么样才算数“较小规模”呢?那就看接下来的“He initialization”。
四.“He initialization”初始化
与随机初始化的人工设置取值规模不同,He initialization有一个专门的公式去自动设置取值规模,如下:

即在使用np.random.randn()取随机值之后,再乘上sqrt(2/layer_dims[l-1])。

# GRADED FUNCTION: initialize_parameters_he def initialize_parameters_he(layers_dims): """ Arguments: layer_dims -- python array (list) containing the size of each layer. Returns: parameters -- python dictionary containing your parameters "W1", "b1", ..., "WL", "bL": W1 -- weight matrix of shape (layers_dims[1], layers_dims[0]) b1 -- bias vector of shape (layers_dims[1], 1) ... WL -- weight matrix of shape (layers_dims[L], layers_dims[L-1]) bL -- bias vector of shape (layers_dims[L], 1) """ # np.random.seed(3) parameters = {} L = len(layers_dims) - 1 # integer representing the number of layers for l in range(1, L + 1): ### START CODE HERE ### (≈ 2 lines of code) parameters['W' + str(l)] = np.random.randn(layers_dims[l],layers_dims[l-1]) * np.sqrt(2/layers_dims[l-1]) parameters['b' + str(l)] = np.zeros((layers_dims[l],1)) ### END CODE HERE ### return parameters
测试效果:
parameters = model(train_X, train_Y, initialization = "he") print ("On the train set:") predictions_train = predict(train_X, train_Y, parameters) print ("On the test set:") predictions_test = predict(test_X, test_Y, parameters)


从曲线可以看出,使用He initialization的训练过程与随机初始化的相比,明显平滑很多,而且最终的准确率也是相当高。这就充分说明了:在深度学习中,一个好的初始化能大大地提高模型的准确率。而He initialization在这方面做得十分出色。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号