吴恩达深度学习笔记(二)—— 深层神经网络的训练过程
主要内容:
一.初始化参数
二.前向传播
三.计算代价函数
四.反向传播
五.更新参数(梯度下降)
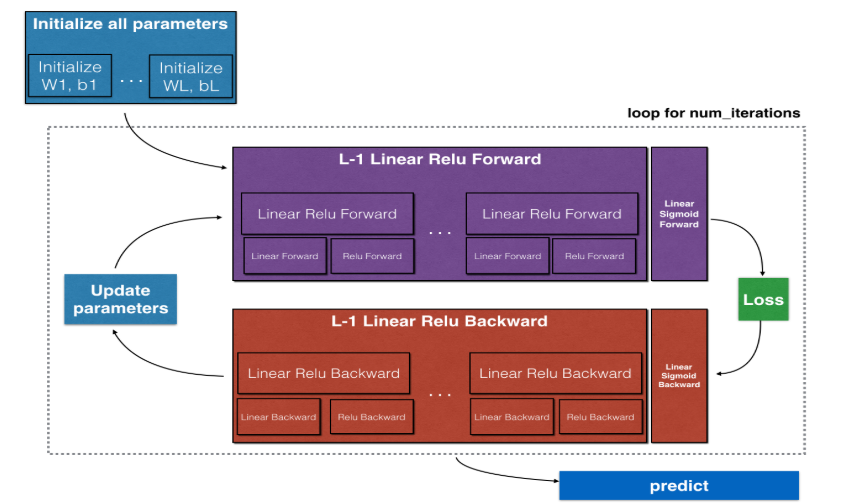
一.初始化参数
1.由于将参数W初始化为0会导致神经网络失效,因而需要对W进行随机初始化。一般的做法是用np.random.np()生成一个高斯分布的数,然后再乘上一个很小的数比如0.01,以限制它的范围。所以可知W的初始值是一个很小的数(绝对值小),那为什么不能取绝对值较大的数呢?根据sigmoid或者tanh函数的图像可知,当z = wx + b 很大或很小时,曲线的斜率很小,这就会导致梯度下降的速度非常慢,不利于快速达到局部最优值。而当w绝对值很大时,z绝对值也会很大,所以w的绝对值值应该尽量小,以保证在初期有较快的梯度下降速度。
2.由于参数b的初始化对神经网络没有较大的影响,因此可以直接设置为0。
3.对于神经网络而言,由于每一层的结点数都可能不一样,这样也就导致了每一层结点上的参数W的形状不一样,这里也是非容易出错,因而需要理每一层网络的参数的形状。假设输入层X有12288个特征,有209个样本,那么这个深度神经网络的参数具体如下(n[l]表示第l层的结点数):
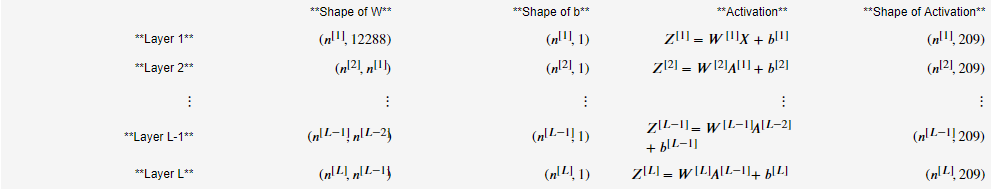
4.代码如下:

#layer_dims为每一层的结点数,包括输入层 def initialize_parameters_deep(layer_dims): """ Arguments: layer_dims -- python array (list) containing the dimensions of each layer in our network Returns: parameters -- python dictionary containing your parameters "W1", "b1", ..., "WL", "bL": Wl -- weight matrix of shape (layer_dims[l], layer_dims[l-1]) bl -- bias vector of shape (layer_dims[l], 1) """ np.random.seed(3) parameters = {} #用字典存储参数W和b L = len(layer_dims) - 1 # 神经网络的层数,不考虑输入层 #初始化第1到第L层结点的参数,其中第0层为输入层X for l in range(1, L+1): ### START CODE HERE ### (≈ 2 lines of code) parameters['W' + str(l)] = np.random.randn(layer_dims[l], layer_dims[l-1]) * 0.01 parameters['b' + str(l)] = np.zeros((layer_dims[l],1)) ### END CODE HERE ### assert(parameters['W' + str(l)].shape == (layer_dims[l], layer_dims[l-1])) assert(parameters['b' + str(l)].shape == (layer_dims[l], 1)) return parameters
二.前向传播
1.前向传播相对简单,对于每一层可分为两个步骤
1)首先计算出线性值:Z[l] = W[l]A[l-1] + b[l]
2)然后将Z[l]带入到激活函数中,作为这一层的输出:A[l] = g(Z[l])
2.在执行这两个步骤时,需要将Z[l]、A[l-1]、W[l]、b[l]存起来,以待反向传播之用。实际上b[l]不是必须的,只不过b[l]可以用来检测db[l]的形状是否正确。
3.对于第1~L-1层,一般使用relu()函数作为激活函数,而对于第L层,一般使用sigmoid()函数,因而sigmoid()函数的输出值是[0,1],可以作为概率。
1)线性计算:

# GRADED FUNCTION: linear_forward def linear_forward(A, W, b): """ Implement the linear part of a layer's forward propagation. Arguments: A -- activations from previous layer (or input data): (size of previous layer, number of examples) W -- weights matrix: numpy array of shape (size of current layer, size of previous layer) b -- bias vector, numpy array of shape (size of the current layer, 1) Returns: Z -- the input of the activation function, also called pre-activation parameter cache -- a python dictionary containing "A", "W" and "b" ; stored for computing the backward pass efficiently """ ### START CODE HERE ### (≈ 1 line of code) Z = np.dot(W,A) + b ### END CODE HERE ### assert(Z.shape == (W.shape[0], A.shape[1])) cache = (A, W, b) return Z, cache
2)单层计算:

# GRADED FUNCTION: linear_activation_forward def linear_activation_forward(A_prev, W, b, activation): """ Implement the forward propagation for the LINEAR->ACTIVATION layer Arguments: A_prev -- activations from previous layer (or input data): (size of previous layer, number of examples) W -- weights matrix: numpy array of shape (size of current layer, size of previous layer) b -- bias vector, numpy array of shape (size of the current layer, 1) activation -- the activation to be used in this layer, stored as a text string: "sigmoid" or "relu" Returns: A -- the output of the activation function, also called the post-activation value cache -- a python dictionary containing "linear_cache" and "activation_cache"; stored for computing the backward pass efficiently """ if activation == "sigmoid": # Inputs: "A_prev, W, b". Outputs: "A, activation_cache". ### START CODE HERE ### (≈ 2 lines of code) Z, linear_cache = linear_forward(A_prev,W,b) A, activation_cache = sigmoid(Z) ### END CODE HERE ### elif activation == "relu": # Inputs: "A_prev, W, b". Outputs: "A, activation_cache". ### START CODE HERE ### (≈ 2 lines of code) Z, linear_cache = linear_forward(A_prev,W,b) A, activation_cache = relu(Z) ### END CODE HERE ### assert (A.shape == (W.shape[0], A_prev.shape[1])) cache = (linear_cache, activation_cache) return A, cache
3)for循环执行前向传播:

# GRADED FUNCTION: L_model_forward def L_model_forward(X, parameters): """ Implement forward propagation for the [LINEAR->RELU]*(L-1)->LINEAR->SIGMOID computation Arguments: X -- data, numpy array of shape (input size, number of examples) parameters -- output of initialize_parameters_deep() Returns: AL -- last post-activation value caches -- list of caches containing: every cache of linear_relu_forward() (there are L-1 of them, indexed from 0 to L-2) the cache of linear_sigmoid_forward() (there is one, indexed L-1) """ caches = [] A = X L = len(parameters) // 2 # number of layers in the neural network,W和b是成对出现的,所以层数是参数的个数/2 # Implement [LINEAR -> RELU]*(L-1). Add "cache" to the "caches" list. for l in range(1, L): ### START CODE HERE ### (≈ 2 lines of code) A, cache = linear_activation_forward(A_prev=A,W=parameters["W"+str(l)],b=parameters["b"+str(l)],activation="relu") caches.append(cache) ### END CODE HERE ### # Implement LINEAR -> SIGMOID. Add "cache" to the "caches" list. ### START CODE HERE ### (≈ 2 lines of code) AL, cache = linear_activation_forward(A_prev=A,W=parameters["W"+str(L)],b=parameters["b"+str(L)],activation="sigmoid") caches.append(cache) ### END CODE HERE ### assert(AL.shape == (1,X.shape[1])) return AL, caches
三.计算代价函数
由于第L层使用的是sigmoid()函数,所以最终的代价函数为:
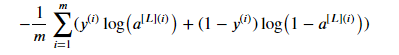
代码如下:
# GRADED FUNCTION: compute_cost def compute_cost(AL, Y): """ Implement the cost function defined by equation (7). Arguments: AL -- probability vector corresponding to your label predictions, shape (1, number of examples) Y -- true "label" vector (for example: containing 0 if non-cat, 1 if cat), shape (1, number of examples) Returns: cost -- cross-entropy cost """ m = Y.shape[1] # Compute loss from aL and y. ### START CODE HERE ### (≈ 1 lines of code) cost = -1/m*np.sum(Y*np.log(AL)+(1-Y)*np.log(1-AL)) ### END CODE HERE ### cost = np.squeeze(cost) # To make sure your cost's shape is what we expect (e.g. this turns [[17]] into 17). assert(cost.shape == ()) return cost
四.反向传播
1.反向传播最主要的作用就是计算出dW、db这两类倒数,用于梯度下降。
2.反向传播的起始是计算出dAL,根据代价函数,对AL进行求导,可得:

3.之后的过程就是:对于第l层,输入dA[l] 和 cache(存储A[l-1]、Z[l]、W[l]、b[l],其中b[l]非必须),输出dA[l-1]、dW[l]、db[l]:
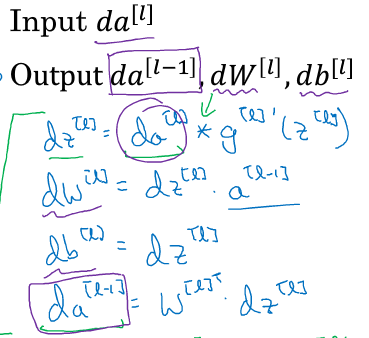
代码如下:

# GRADED FUNCTION: linear_activation_backward def linear_activation_backward(dA, cache, activation): """ Implement the backward propagation for the LINEAR->ACTIVATION layer. Arguments: dA -- post-activation gradient for current layer l cache -- tuple of values (linear_cache, activation_cache) we store for computing backward propagation efficiently activation -- the activation to be used in this layer, stored as a text string: "sigmoid" or "relu" Returns: dA_prev -- Gradient of the cost with respect to the activation (of the previous layer l-1), same shape as A_prev dW -- Gradient of the cost with respect to W (current layer l), same shape as W db -- Gradient of the cost with respect to b (current layer l), same shape as b """ linear_cache, activation_cache = cache if activation == "relu": ### START CODE HERE ### (≈ 2 lines of code) dZ = relu_backward(dA, activation_cache) #dA乘上dA对Z的导数,得到dZ。需要根据不同的激活函数而定,因而在这里封装起来 dA_prev, dW, db = linear_backward(dZ=dZ,cache=linear_cache) ### END CODE HERE ### elif activation == "sigmoid": ### START CODE HERE ### (≈ 2 lines of code) dZ = sigmoid_backward(dA, activation_cache) dA_prev, dW, db = linear_backward(dZ=dZ,cache=linear_cache) ### END CODE HERE ### return dA_prev, dW, db
4.整个过程如下:
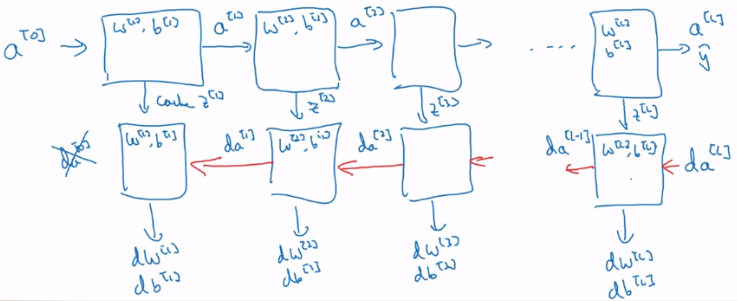
代码如下:

# GRADED FUNCTION: L_model_backward def L_model_backward(AL, Y, caches): """ Implement the backward propagation for the [LINEAR->RELU] * (L-1) -> LINEAR -> SIGMOID group Arguments: AL -- probability vector, output of the forward propagation (L_model_forward()) Y -- true "label" vector (containing 0 if non-cat, 1 if cat) caches -- list of caches containing: every cache of linear_activation_forward() with "relu" (it's caches[l], for l in range(L-1) i.e l = 0...L-2) the cache of linear_activation_forward() with "sigmoid" (it's caches[L-1]) Returns: grads -- A dictionary with the gradients grads["dA" + str(l)] = ... grads["dW" + str(l)] = ... grads["db" + str(l)] = ... """ grads = {} L = len(caches) # the number of layers m = AL.shape[1] Y = Y.reshape(AL.shape) # after this line, Y is the same shape as AL # Initializing the backpropagation ### START CODE HERE ### (1 line of code) dAL = - (np.divide(Y, AL) - np.divide(1 - Y, 1 - AL)) ### END CODE HERE ### # Lth layer (SIGMOID -> LINEAR) gradients. Inputs: "DAL, Y, caches". Outputs: "grads["dAL-1"], grads["dWL"], grads["dbL"] ### START CODE HERE ### (approx. 2 lines) #计算第L层,分开计算是因为激活函数不同 current_cache = caches[L-1] #注意caches的下标从0开始,而网络层从1开始,所以第L层的缓存对应caches[L-1] grads["dA" + str(L-1)], grads["dW" + str(L)], grads["db" + str(L)] = linear_activation_backward(dAL, current_cache, activation = 'sigmoid') ### END CODE HERE ### #从第L-1层计算到第一层: for l in reversed(range(1,L)): # Inputs: "grads["dA" + str(l)], caches". Outputs: "grads["dA" + str(l - 1)] , grads["dW" + str(l)] , grads["db" + str(l)] ### START CODE HERE ### (approx. 5 lines) current_cache = caches[l-1] #注意caches的下标从0开始,而网络层从1开始,所以第L层的缓存对应caches[l-1] dA_prev_temp, dW_temp, db_temp = linear_activation_backward(grads["dA"+str(l)],current_cache,"relu") grads["dA" + str(l-1)] = dA_prev_temp grads["dW" + str(l)] = dW_temp grads["db" + str(l)] = db_temp ### END CODE HERE ### return grads
五.更新参数(梯度下降)
通过反向传播求出dW、db之后,剩下的工作就相对轻松了,直接进行梯度下降,更新参数:

代码如下(没有进行正则化):
# GRADED FUNCTION: update_parameters def update_parameters(parameters, grads, learning_rate): """ Update parameters using gradient descent Arguments: parameters -- python dictionary containing your parameters grads -- python dictionary containing your gradients, output of L_model_backward Returns: parameters -- python dictionary containing your updated parameters parameters["W" + str(l)] = ... parameters["b" + str(l)] = ... """ L = len(parameters) // 2 # number of layers in the neural network # Update rule for each parameter. Use a for loop. ### START CODE HERE ### (≈ 3 lines of code) for l in range(L): parameters["W" + str(l+1)] = parameters["W" + str(l+1)] - learning_rate*grads["dW" + str(l+1)] parameters["b" + str(l+1)] = parameters["b" + str(l+1)] - learning_rate*grads["db" + str(l+1)] ### END CODE HERE ### return parameters



 浙公网安备 33010602011771号
浙公网安备 33010602011771号