POJ3415 Common Substrings —— 后缀数组 + 单调栈 公共子串个数

题目链接：https://vjudge.net/problem/POJ-3415

 

Common Substrings
Time Limit: 5000MS   Memory Limit: 65536K
Total Submissions: 12240   Accepted: 4144

Description

A substring of a string T is defined as:

 

T(i, k)=TiTi+1...Ti+k-1, 1≤i≤i+k-1≤|T|.

 

Given two strings A, B and one integer K, we define S, a set of triples (i, j, k):

 

S = {(i, j, k) | k≥K, A(i, k)=B(j, k)}.

 

You are to give the value of |S| for specific A, B and K.

Input

The input file contains several blocks of data. For each block, the first line contains one integer K, followed by two lines containing strings A and B, respectively. The input file is ended by K=0.

1 ≤ |A|, |B| ≤ 105
1 ≤ K ≤ min{|A|, |B|}
Characters of A and B are all Latin letters.

 

Output

For each case, output an integer |S|.

Sample Input

2
aababaa
abaabaa
1
xx
xx
0

Sample Output

22
5

Source

POJ Monthly--2007.10.06, wintokk

 

题意：

给出两个字符串，求有多少对长度不小于k的公共子串，子串相同但位置不同也单独算作一对。

 

题解：

1.将两个字符串拼接在一起，中间用分隔符隔开，得到新串。并且需要记录每个位置上的字符（后缀）属于哪一个字符串。

2.求出新串的后缀数组。可知sa[i]和sa[j]的最长公共前缀为：min（height[k]）i+1<=k<=j。

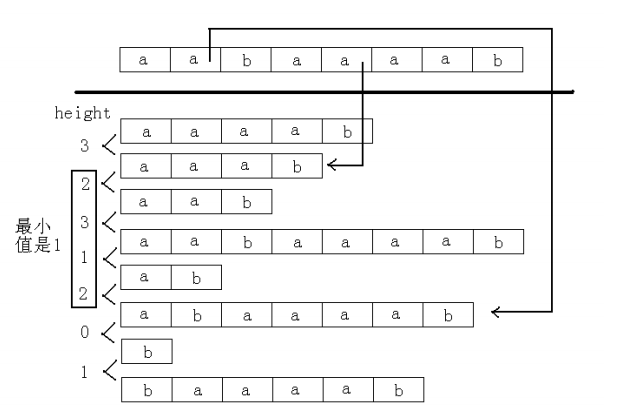
3.根据第二点，可以枚举sa数组，当遇到A串时，就先放着，当遇到B串时，就往前统计与所有A串的最长公共前缀，假如为len，那么就能增加len-k+1个公共前缀了。由于是按着sa的顺序枚举下去的，所以对于在B串下面的A串是没有统计到的，所以需要二次统计：把A串当成B串， B串当成A串，然后再进行统计，方可无遗漏。

4.往前统计时需要用到单调栈。

 

代码如下：

  1 #include <iostream>
  2 #include <cstdio>
  3 #include <cstring>
  4 #include <algorithm>
  5 #include <vector>
  6 #include <cmath>
  7 #include <queue>
  8 #include <stack>
  9 #include <map>
 10 #include <string>
 11 #include <set>
 12 using namespace std;
 13 typedef long long LL;
 14 const int INF = 2e9;
 15 const LL LNF = 9e18;
 16 const int MOD = 1e9+7;
 17 const int MAXN = 2e5+100;
 18 
 19 int id[MAXN];
 20 int r[MAXN], sa[MAXN], Rank[MAXN], height[MAXN];
 21 int t1[MAXN], t2[MAXN], c[MAXN];
 22 
 23 bool cmp(int *r, int a, int b, int l)
 24 {
 25     return r[a]==r[b] && r[a+l]==r[b+l];
 26 }
 27 
 28 void DA(int str[], int sa[], int Rank[], int height[], int n, int m)
 29 {
 30     n++;
 31     int i, j, p, *x = t1, *y = t2;
 32     for(i = 0; i<m; i++) c[i] = 0;
 33     for(i = 0; i<n; i++) c[x[i] = str[i]]++;
 34     for(i = 1; i<m; i++) c[i] += c[i-1];
 35     for(i = n-1; i>=0; i--) sa[--c[x[i]]] = i;
 36     for(j = 1; j<=n; j <<= 1)
 37     {
 38         p = 0;
 39         for(i = n-j; i<n; i++) y[p++] = i;
 40         for(i = 0; i<n; i++) if(sa[i]>=j) y[p++] = sa[i]-j;
 41 
 42         for(i = 0; i<m; i++) c[i] = 0;
 43         for(i = 0; i<n; i++) c[x[y[i]]]++;
 44         for(i = 1; i<m; i++) c[i] += c[i-1];
 45         for(i = n-1; i>=0; i--) sa[--c[x[y[i]]]] = y[i];
 46 
 47         swap(x, y);
 48         p = 1; x[sa[0]] = 0;
 49         for(i = 1; i<n; i++)
 50             x[sa[i]] = cmp(y, sa[i-1], sa[i], j)?p-1:p++;
 51 
 52         if(p>=n) break;
 53         m = p;
 54     }
 55 
 56     int k = 0;
 57     n--;
 58     for(i = 0; i<=n; i++) Rank[sa[i]] = i;
 59     for(i = 0; i<n; i++)
 60     {
 61         if(k) k--;
 62         j = sa[Rank[i]-1];
 63         while(str[i+k]==str[j+k]) k++;
 64         height[Rank[i]] = k;
 65     }
 66 }
 67 
 68 int Stack[MAXN][2], top;
 69 LL cal(int k, int len, int flag)
 70 {
 71     LL sum = 0, tmp = 0;
 72     top = 0;
 73     for(int i = 2; i<=len; i++)
 74     {
 75         if(height[i]<k)
 76             tmp = top = 0;
 77         else
 78         {
 79             int cnt = 0;
 80             if(id[sa[i-1]]==flag)
 81                 tmp += height[i]-k+1, cnt++;
 82             while(top>0 && height[i]<=Stack[top-1][0])
 83             {
 84                 tmp -= 1LL*Stack[top-1][1]*(Stack[top-1][0]-height[i]);
 85                 cnt += Stack[top-1][1];
 86                 top--;
 87             }
 88             Stack[top][0] = height[i];
 89             Stack[top++][1] = cnt;
 90             if(id[sa[i]]!=flag)
 91                 sum += tmp;
 92         }
 93     }
 94     return sum;
 95 }
 96 
 97 char str[MAXN];
 98 int main()
 99 {
100     int k;
101     while(scanf("%d",&k)&&k)
102     {
103         int len = 0;
104         scanf("%s", str);
105         int LEN = strlen(str);
106         for(int j = 0; j<LEN; j++)
107         {
108             r[len] = str[j];
109             id[len++] = 0;
110         }
111         r[len] = '$';
112         id[len++] = 0;
113         scanf("%s", str);
114         LEN = strlen(str);
115         for(int j = 0; j<LEN; j++)
116         {
117             r[len] = str[j];
118             id[len++] = 1;
119         }
120         r[len] = 0;
121         DA(r,sa,Rank,height,len,130);
122         cout<< cal(k,len,0)+cal(k,len,1) <<endl;
123     }
124 }
View Code

 

posted on 2018-02-26 18:17  h_z_cong  阅读(190)  评论(0)  编辑  收藏  举报

导航