SPOJ - REPEATS —— 后缀数组 重复次数最多的连续重复子串

题目链接：https://vjudge.net/problem/SPOJ-REPEATS

 

REPEATS - Repeats

no tags 

 

A string s is called an (k,l)-repeat if s is obtained by concatenating k>=1 times some seed string t with length l>=1. For example, the string

s = abaabaabaaba

is a (4,3)-repeat with t = aba as its seed string. That is, the seed string t is 3 characters long, and the whole string s is obtained by repeating t 4 times.

Write a program for the following task: Your program is given a long string u consisting of characters ‘a’ and/or ‘b’ as input. Your program must find some (k,l)-repeat that occurs as substring within u with k as large as possible. For example, the input string

u = babbabaabaabaabab

contains the underlined (4,3)-repeat s starting at position 5. Since u contains no other contiguous substring with more than 4 repeats, your program must output the maximum k.

 

Input

In the first line of the input contains H- the number of test cases (H <= 20). H test cases follow. First line of each test cases is n - length of the input string (n <= 50000), The next n lines contain the input string, one character (either ‘a’ or ‘b’) per line, in order.

Output

For each test cases, you should write exactly one interger k in a line - the repeat count that is maximized.

Example

Input:
1
17
b
a
b
b
a
b
a
a
b
a
a
b
a
a
b
a
b

Output:
4

since a (4, 3)-repeat is found starting at the 5th character of the input string.

 

 

题意：

给出一个字符串，求该字符串的重复次数最多的连续重复子串，输出重复次数。

 

题解：

论文上面的题。

 

 

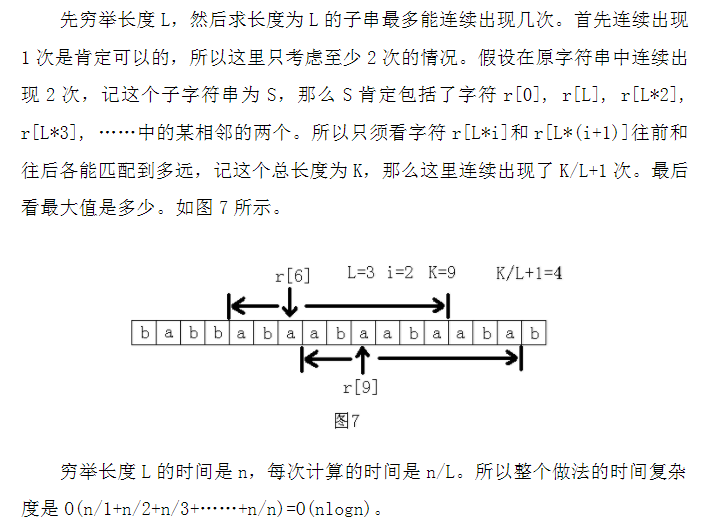
代码如下：

#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <vector>
#include <cmath>
#include <queue>
#include <stack>
#include <map>
#include <string>
#include <set>
using namespace std;
typedef long long LL;
const int INF = 2e9;
const LL LNF = 9e18;
const int MOD = 1e9+7;
const int MAXN = 5e4+100;

bool cmp(int *r, int a, int b, int l)
{
    return r[a]==r[b] && r[a+l]==r[b+l];
}

int r[MAXN], sa[MAXN], Rank[MAXN], height[MAXN];
int t1[MAXN], t2[MAXN], c[MAXN];
void DA(int str[], int sa[], int Rank[], int height[], int n, int m)
{
    n++;
    int i, j, p, *x = t1, *y = t2;
    for(i = 0; i<m; i++) c[i] = 0;
    for(i = 0; i<n; i++) c[x[i] = str[i]]++;
    for(i = 1; i<m; i++) c[i] += c[i-1];
    for(i = n-1; i>=0; i--) sa[--c[x[i]]] = i;
    for(j = 1; j<=n; j <<= 1)
    {
        p = 0;
        for(i = n-j; i<n; i++) y[p++] = i;
        for(i = 0; i<n; i++) if(sa[i]>=j) y[p++] = sa[i]-j;

        for(i = 0; i<m; i++) c[i] = 0;
        for(i = 0; i<n; i++) c[x[y[i]]]++;
        for(i = 1; i<m; i++) c[i] += c[i-1];
        for(i = n-1; i>=0; i--) sa[--c[x[y[i]]]] = y[i];

        swap(x, y);
        p = 1; x[sa[0]] = 0;
        for(i = 1; i<n; i++)
            x[sa[i]] = cmp(y, sa[i-1], sa[i], j)?p-1:p++;

        if(p>=n) break;
        m = p;
    }

    int k = 0;
    n--;
    for(i = 0; i<=n; i++) Rank[sa[i]] = i;
    for(i = 0; i<n; i++)
    {
        if(k) k--;
        j = sa[Rank[i]-1];
        while(str[i+k]==str[j+k]) k++;
        height[Rank[i]] = k;
    }
}

int dp[MAXN][20], mm[MAXN];
void initRMQ(int n, int b[])
{
    mm[0] = -1;
    for(int i = 1; i<=n; i++)
        dp[i][0] = b[i], mm[i] = ((i&(i-1))==0)?mm[i-1]+1:mm[i-1];
    for(int j = 1; j<=mm[n]; j++)
    for(int i = 1; i+(1<<j)-1<=n; i++)
        dp[i][j] = min(dp[i][j-1], dp[i+(1<<(j-1))][j-1]);
}

int RMQ(int x, int y)
{
    if(x>y) swap(x, y);
    x++;
    int k = mm[y-x+1];
    return min(dp[x][k], dp[y-(1<<k)+1][k]);
}

int main()
{
    int T, n;
    scanf("%d", &T);
    while(T--)
    {
        scanf("%d", &n);
        for(int i = 0; i<n; i++)
        {
            char ch;
            getchar();
            scanf("%c", &ch);
            r[i] = ch-'a'+1;
        }
        r[n] = 0;
        DA(r, sa, Rank, height, n, 3);
        initRMQ(n, height);

        int times = 0, L, R;
        for(int len = 1; len<=n; len++)
        for(int pos = 0; pos+len<n; pos += len)
        {
            int LCP = RMQ(Rank[pos], Rank[pos+len]);
            int supplement = len - LCP%len;
            int k = pos - supplement;
            if(k>=0 && LCP%len && RMQ(Rank[k],Rank[k+len])>=supplement)
                LCP += supplement;
            times = max(times, LCP/len+1);
        }
        printf("%d\n", times);
    }
}