HDU3338 Kakuro Extension —— 最大流、方格填数类似数独

题目链接：https://vjudge.net/problem/HDU-3338

Kakuro Extension

Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others)
Total Submission(s): 2419 Accepted Submission(s): 840
Special Judge

Problem Description

If you solved problem like this, forget it.Because you need to use a completely different algorithm to solve the following one.
Kakuro puzzle is played on a grid of "black" and "white" cells. Apart from the top row and leftmost column which are entirely black, the grid has some amount of white cells which form "runs" and some amount of black cells. "Run" is a vertical or horizontal maximal one-lined block of adjacent white cells. Each row and column of the puzzle can contain more than one "run". Every white cell belongs to exactly two runs — one horizontal and one vertical run. Each horizontal "run" always has a number in the black half-cell to its immediate left, and each vertical "run" always has a number in the black half-cell immediately above it. These numbers are located in "black" cells and are called "clues".The rules of the puzzle are simple:

1.place a single digit from 1 to 9 in each "white" cell
2.for all runs, the sum of all digits in a "run" must match the clue associated with the "run"

Given the grid, your task is to find a solution for the puzzle.
　　　　　　　　

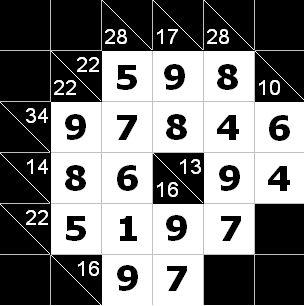
　　　　　　　　Picture of the first sample input　　　　　　　　　　　　Picture of the first sample output

Input

The first line of input contains two integers n and m (2 ≤ n,m ≤ 100) — the number of rows and columns correspondingly. Each of the next n lines contains descriptions of m cells. Each cell description is one of the following 7-character strings:

.......— "white" cell;
XXXXXXX— "black" cell with no clues;
AAA\BBB— "black" cell with one or two clues. AAA is either a 3-digit clue for the corresponding vertical run, or XXX if there is no associated vertical run. BBB is either a 3-digit clue for the corresponding horizontal run, or XXX if there is no associated horizontal run.
The first row and the first column of the grid will never have any white cells. The given grid will have at least one "white" cell.It is guaranteed that the given puzzle has at least one solution.

Output

Print n lines to the output with m cells in each line. For every "black" cell print '_' (underscore), for every "white" cell print the corresponding digit from the solution. Delimit cells with a single space, so that each row consists of 2m-1 characters.If there are many solutions, you may output any of them.

Sample Input

6 6 XXXXXXX XXXXXXX 028\XXX 017\XXX 028\XXX XXXXXXX XXXXXXX 022\022 ....... ....... ....... 010\XXX XXX\034 ....... ....... ....... ....... ....... XXX\014 ....... ....... 016\013 ....... ....... XXX\022 ....... ....... ....... ....... XXXXXXX XXXXXXX XXX\016 ....... ....... XXXXXXX XXXXXXX 5 8 XXXXXXX 001\XXX 020\XXX 027\XXX 021\XXX 028\XXX 014\XXX 024\XXX XXX\035 ....... ....... ....... ....... ....... ....... ....... XXXXXXX 007\034 ....... ....... ....... ....... ....... ....... XXX\043 ....... ....... ....... ....... ....... ....... ....... XXX\030 ....... ....... ....... ....... ....... ....... XXXXXXX

Sample Output

_ _ _ _ _ _ _ _ 5 8 9 _ _ 7 6 9 8 4 _ 6 8 _ 7 6 _ 9 2 7 4 _ _ _ 7 9 _ _ _ _ _ _ _ _ _ _ _ 1 9 9 1 1 8 6 _ _ 1 7 7 9 1 9 _ 1 3 9 9 9 3 9 _ 6 7 2 4 9 2 _

Author

NotOnlySuccess@HDU

Source

HDOJ Monthly Contest – 2010.03.06

题意：

给定一个n*m的矩阵，为其中的白格填上范围为1~9的数，并且满足横之和、纵之和的限制，限制记录在黑格子上。类似于数独游戏，要求输出一组可行解。

题解：

可知横之和的和必定等于纵之和的和，因为横之和的和是所有白格子的和， so does 纵之和的和。因此，我们可以用网络流来解题，建图如下：

1.先对行进行分块，然后再对列进行分块，因为同一行或同一列不一定属于同一个run。

2.建立超级源点，超级源点连向每一个横之和结点，容量为横之和。

3.对于每个白格，将其横坐标所属的横之和结点连向其纵坐标所属的纵之和结点，容量下界为1，容量上界为9。

4.建立超级汇点，每个纵之和结点连向超级汇点，容量为纵之和。

5.回顾上述建图方法，发现白格建的边容量下界（一般情况都是没有下界的，即为0），不好处理。但是可以知道容量下界都为1，那么，我们可以先为每个白格子都分一个1，表明这个1是必须的，毋庸置疑。因此，就可以去掉白格子所建的边的容量下界了，而容量上界也因此改为8.

6.由于“横之和的和=纵之和的和”，“横之和的和”的流量由超级源点发出，“纵之和的和”的流量由超级汇点接收，且可知如果有解，那么白格子的存在（调节）必定能使每条：超级汇点-->“横之和”结点的边满流，而满流时必定是最大流。因此我们可以跑最大流算法，然后再提取每条白格子所建边的流量信息，即可知道每个白格子应该填上什么数。

写法一：

  1 #include <iostream>
  2 #include <cstdio>
  3 #include <cstring>
  4 #include <algorithm>
  5 #include <vector>
  6 #include <cmath>
  7 #include <queue>
  8 #include <stack>
  9 #include <map>
 10 #include <string>
 11 #include <set>
 12 using namespace std;
 13 typedef long long LL;
 14 const int INF = 2e9;
 15 const LL LNF = 9e18;
 16 const int mod = 1e9+7;
 17 const int MAXM = 1e5+10;
 18 const int MAXN = 1e4+10;
 19 
 20 struct Edge
 21 {
 22     int to, next, cap, flow;
 23 }edge[MAXM];
 24 int tot, head[MAXN];
 25 int gap[MAXN], dep[MAXN], pre[MAXN], cur[MAXN];
 26 
 27 void init()
 28 {
 29     tot = 0;
 30     memset(head, -1, sizeof(head));
 31 }
 32 
 33 void add(int u, int v, int w)
 34 {
 35     edge[tot].to = v; edge[tot].cap = w; edge[tot].flow = 0;
 36     edge[tot].next = head[u]; head[u] = tot++;
 37     edge[tot].to = u; edge[tot].cap = 0; edge[tot].flow = 0;
 38     edge[tot].next = head[v]; head[v] = tot++;
 39 }
 40 
 41 int sap(int start, int end, int nodenum)
 42 {
 43     memset(dep, 0, sizeof(dep));
 44     memset(gap, 0, sizeof(gap));
 45     memcpy(cur, head, sizeof(head));
 46     int u = pre[start] = start, maxflow = 0,aug = INF;
 47     gap[0] = nodenum;
 48     while(dep[start]<nodenum)
 49     {
 50         loop:
 51         for(int i = cur[u]; i!=-1; i = edge[i].next)
 52         {
 53             int v = edge[i].to;
 54             if(edge[i].cap-edge[i].flow && dep[u]==dep[v]+1)
 55             {
 56                 aug = min(aug, edge[i].cap-edge[i].flow);
 57                 pre[v] = u;
 58                 cur[u] = i;
 59                 u = v;
 60                 if(v==end)
 61                 {
 62                     maxflow += aug;
 63                     for(u = pre[u]; v!=start; v = u,u = pre[u])
 64                     {
 65                         edge[cur[u]].flow += aug;
 66                         edge[cur[u]^1].flow -= aug;
 67                     }
 68                     aug = INF;
 69                 }
 70                 goto loop;
 71             }
 72         }
 73         int mindis = nodenum;
 74         for(int i = head[u]; i!=-1; i = edge[i].next)
 75         {
 76             int v=edge[i].to;
 77             if(edge[i].cap-edge[i].flow && mindis>dep[v])
 78             {
 79                 cur[u] = i;
 80                 mindis = dep[v];
 81             }
 82         }
 83         if((--gap[dep[u]])==0)break;
 84         gap[dep[u]=mindis+1]++;
 85         u = pre[u];
 86     }
 87     return maxflow;
 88 }
 89 
 90 char str[110];
 91 int Map[110][110], run[110][110][2];    //用于记录原始图案
 92 int xid[110][110], yid[110][110];
 93 int xrun[11000], yrun[11000], index[110][110];
 94 int main()
 95 {
 96     int n, m;
 97     while(scanf("%d%d", &n,&m)!=EOF)
 98     {
 99         for(int i = 1; i<=n; i++)
100         for(int j = 1; j<=m; j++)
101         {
102             scanf("%s", str);
103             if(str[0]=='.') Map[i][j] = 1;
104             else
105             {
106                 Map[i][j] = 0;
107                 if(str[0]!='X') run[i][j][0] = (str[0]-'0')*100+(str[1]-'0')*10+(str[2]-'0');
108                 if(str[4]!='X') run[i][j][1] = (str[4]-'0')*100+(str[5]-'0')*10+(str[6]-'0');
109             }
110         }
111 
112         int xcnt = 0, ycnt = 0;
113         for(int i = 2; i<=n; i++)
114         for(int j = 2; j<=m; j++)
115         {
116             if(Map[i][j])
117             {
118                 if(!Map[i][j-1])    //横流
119                 {
120                     xid[i][j] = xcnt;
121                     xrun[xcnt++] = run[i][j-1][1];
122                 }else xid[i][j] = xid[i][j-1];
123                 xrun[xid[i][j]]--;
124 
125                 if(!Map[i-1][j])    //纵流
126                 {
127                     yid[i][j] = ycnt;
128                     yrun[ycnt++] = run[i-1][j][0];
129                 }else yid[i][j] = yid[i-1][j];
130                 yrun[yid[i][j]]--;
131             }
132         }
133 
134         int start = xcnt+ycnt, end = xcnt+ycnt+1;
135         init();
136         for(int i = 2; i<=n; i++)
137         for(int j = 2; j<=m; j++)
138         {
139             if(Map[i][j])
140             {
141                 add(xid[i][j], xcnt+yid[i][j], 8);
142                 index[i][j] = tot-2;    //记录这个空格所对应的边
143             }
144         }
145         for(int i = 0; i<xcnt; i++) add(start, i, xrun[i]);
146         for(int i = 0; i<ycnt; i++) add(xcnt+i, end, yrun[i]);
147 
148         sap(start, end, xcnt+ycnt+2);
149         for(int i = 1; i<=n; i++)
150         {
151             for(int j = 1; j<=m; j++)
152             {
153                 printf("%c", Map[i][j]?(edge[index[i][j]].flow+'1'):'_');
154                 if(j<m) printf(" ");
155             }
156             printf("\n");
157         }
158     }
159 }

View Code

写法二：

  1 #include <iostream>
  2 #include <cstdio>
  3 #include <cstring>
  4 #include <algorithm>
  5 #include <vector>
  6 #include <cmath>
  7 #include <queue>
  8 #include <stack>
  9 #include <map>
 10 #include <string>
 11 #include <set>
 12 using namespace std;
 13 typedef long long LL;
 14 const int INF = 2e9;
 15 const LL LNF = 9e18;
 16 const int mod = 1e9+7;
 17 const int MAXM = 1e5+10;
 18 const int MAXN = 1e4+10;
 19 
 20 struct Edge
 21 {
 22     int to, next, cap, flow;
 23 }edge[MAXM];
 24 int tot, head[MAXN];
 25 int gap[MAXN], dep[MAXN], pre[MAXN], cur[MAXN];
 26 
 27 void init()
 28 {
 29     tot = 0;
 30     memset(head, -1, sizeof(head));
 31 }
 32 
 33 void add(int u, int v, int w)
 34 {
 35     edge[tot].to = v; edge[tot].cap = w; edge[tot].flow = 0;
 36     edge[tot].next = head[u]; head[u] = tot++;
 37     edge[tot].to = u; edge[tot].cap = 0; edge[tot].flow = 0;
 38     edge[tot].next = head[v]; head[v] = tot++;
 39 }
 40 
 41 int sap(int start, int end, int nodenum)
 42 {
 43     memset(dep, 0, sizeof(dep));
 44     memset(gap, 0, sizeof(gap));
 45     memcpy(cur, head, sizeof(head));
 46     int u = pre[start] = start, maxflow = 0,aug = INF;
 47     gap[0] = nodenum;
 48     while(dep[start]<nodenum)
 49     {
 50         loop:
 51         for(int i = cur[u]; i!=-1; i = edge[i].next)
 52         {
 53             int v = edge[i].to;
 54             if(edge[i].cap-edge[i].flow && dep[u]==dep[v]+1)
 55             {
 56                 aug = min(aug, edge[i].cap-edge[i].flow);
 57                 pre[v] = u;
 58                 cur[u] = i;
 59                 u = v;
 60                 if(v==end)
 61                 {
 62                     maxflow += aug;
 63                     for(u = pre[u]; v!=start; v = u,u = pre[u])
 64                     {
 65                         edge[cur[u]].flow += aug;
 66                         edge[cur[u]^1].flow -= aug;
 67                     }
 68                     aug = INF;
 69                 }
 70                 goto loop;
 71             }
 72         }
 73         int mindis = nodenum;
 74         for(int i = head[u]; i!=-1; i = edge[i].next)
 75         {
 76             int v=edge[i].to;
 77             if(edge[i].cap-edge[i].flow && mindis>dep[v])
 78             {
 79                 cur[u] = i;
 80                 mindis = dep[v];
 81             }
 82         }
 83         if((--gap[dep[u]])==0)break;
 84         gap[dep[u]=mindis+1]++;
 85         u = pre[u];
 86     }
 87     return maxflow;
 88 }
 89 
 90 char str[110];
 91 int Map[110][110], run[110][110][2];
 92 int xid[110][110], yid[110][110];
 93 int xbelong[11000], ybelong[11000], xrun[11000], yrun[11000];
 94 int result[110][110];
 95 int main()
 96 {
 97     int n, m;
 98     while(scanf("%d%d", &n,&m)!=EOF)
 99     {
100         for(int i = 1; i<=n; i++)
101         for(int j = 1; j<=m; j++)
102         {
103             scanf("%s", str);
104             if(str[0]=='.') Map[i][j] = 1;
105             else
106             {
107                 Map[i][j] = 0;
108                 if(str[0]!='X') run[i][j][0] = (str[0]-'0')*100+(str[1]-'0')*10+(str[2]-'0');
109                 if(str[4]!='X') run[i][j][1] = (str[4]-'0')*100+(str[5]-'0')*10+(str[6]-'0');
110             }
111         }
112 
113         int xcnt = 0, ycnt = 0;
114         for(int i = 2; i<=n; i++)
115         for(int j = 2; j<=m; j++)
116         {
117             if(Map[i][j])
118             {
119                 if(!Map[i][j-1])
120                 {
121                     xid[i][j] = xcnt;
122                     xrun[xcnt] = run[i][j-1][1];
123                     xbelong[xcnt++] = i;
124                 }else xid[i][j] = xid[i][j-1];
125                 xrun[xid[i][j]]--;
126 
127                 if(!Map[i-1][j])
128                 {
129                     yid[i][j] = ycnt;
130                     yrun[ycnt] = run[i-1][j][0];
131                     ybelong[ycnt++] = j;
132                 }else yid[i][j] = yid[i-1][j];
133                 yrun[yid[i][j]]--;
134             }
135         }
136 
137         int start = xcnt+ycnt, end = xcnt+ycnt+1;
138         init();
139         for(int i = 2; i<=n; i++)
140         for(int j = 2; j<=m; j++)
141         {
142             if(Map[i][j])
143                 add(xid[i][j], xcnt+yid[i][j], 8);
144         }
145         for(int i = 0; i<xcnt; i++) add(start, i, xrun[i]);
146         for(int i = 0; i<ycnt; i++) add(xcnt+i, end, yrun[i]);
147 
148         sap(start, end, xcnt+ycnt+2);
149         memset(result, 0, sizeof(result));
150 
151         for(int u = 0; u<xcnt; u++)
152         for(int i = head[u]; i!=-1; i=edge[i].next)
153         {
154             int v = edge[i].to-xcnt;
155             if(v>=ycnt) continue;
156             int x = xbelong[u], y = ybelong[v];
157             if(Map[x][y]) result[x][y] = edge[i].flow+1;
158         }
159 
160         for(int i = 1; i<=n; i++)
161         {
162             for(int j = 1; j<=m; j++)
163             {
164                 if(Map[i][j]) printf("%d", result[i][j]);
165                 else  printf("_");
166                 if(j<m) printf(" ");
167             }
168             printf("\n");
169         }
170     }
171 }

View Code

posted on 2017-12-29 21:58 h_z_cong 阅读(419) 评论(0) 编辑收藏举报

刷新页面返回顶部

HDU3338 Kakuro Extension —— 最大流、方格填数类似数独

Kakuro Extension

导航

公告