POJ1456 Supermarket —— 贪心 + 路径压缩优化

题目链接：http://poj.org/problem?id=1456

 

Supermarket

Time Limit: 2000MS		Memory Limit: 65536K
Total Submissions: 13736		Accepted: 6206

Description

A supermarket has a set Prod of products on sale. It earns a profit px for each product x∈Prod sold by a deadline dx that is measured as an integral number of time units starting from the moment the sale begins. Each product takes precisely one unit of time for being sold. A selling schedule is an ordered subset of products Sell ≤ Prod such that the selling of each product x∈Sell, according to the ordering of Sell, completes before the deadline dx or just when dx expires. The profit of the selling schedule is Profit(Sell)=Σ_x∈Sellpx. An optimal selling schedule is a schedule with a maximum profit. 
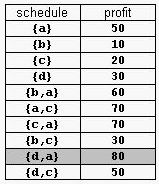
For example, consider the products Prod={a,b,c,d} with (pa,da)=(50,2), (pb,db)=(10,1), (pc,dc)=(20,2), and (pd,dd)=(30,1). The possible selling schedules are listed in table 1. For instance, the schedule Sell={d,a} shows that the selling of product d starts at time 0 and ends at time 1, while the selling of product a starts at time 1 and ends at time 2. Each of these products is sold by its deadline. Sell is the optimal schedule and its profit is 80. 

Write a program that reads sets of products from an input text file and computes the profit of an optimal selling schedule for each set of products. 

Input

A set of products starts with an integer 0 <= n <= 10000, which is the number of products in the set, and continues with n pairs pi di of integers, 1 <= pi <= 10000 and 1 <= di <= 10000, that designate the profit and the selling deadline of the i-th product. White spaces can occur freely in input. Input data terminate with an end of file and are guaranteed correct.

Output

For each set of products, the program prints on the standard output the profit of an optimal selling schedule for the set. Each result is printed from the beginning of a separate line.

Sample Input

4  50 2  10 1   20 2   30 1

7  20 1   2 1   10 3  100 2   8 2
   5 20  50 10

Sample Output

80
185

Hint

The sample input contains two product sets. The first set encodes the products from table 1. The second set is for 7 products. The profit of an optimal schedule for these products is 185.

Source

Southeastern Europe 2003

 

 

 

题解：

1.由于每种商品只需销售一天（要是天数不确定又该怎么办？），且一天只能销售一种商品。所以，在某一天，销售的商品的获利越大越好。

2.对于一种商品，应该尽可能把它推到过期前才销售，这样就可以腾出时间卖其他商品，使获利最大化。

3.贪心：根据商品的获利进行降序排序，用数组used[]标记某一天是否已经确定要卖商品。对每一件商品进行操作：对于该商品，首选的出售时间是deadline，如果deadline已经被其他商品占用了（该商品的获利更大），那么就往前找，找到第一个能用的天，然后将该天标记。

4.对于怎样找到第一个能用的天，有两种方法。第一种方法，也是最直接最暴力的：往前枚举，在此不细述。第二种方法是利用：并查集的路径压缩。

 

并查集的路径压缩： 

1.初始化每一天为可用，即fa[x] = -1。

2.在处理的过程中，如果某一天day被这个商品用了，那么就将fa[day]设为day-1表明：后面的商品如果想用这一天，是行不通的，只能用前面的天，那究竟是哪一天呢？day这一天，作为一个“好心人”，已经为商品指明了方向：去找fa[day]，如果fa[day]也用了，那就去找fa[fa[day]]……直到找到能用的天。

3.利用并查集的路径压缩，在搜索路径上的点，都直接指向了根节点（根节点即为可用的一天），从而减少了搜索长度。

 

 

枚举：

#include <iostream>
#include <cstdio>
#include <cstring>
#include <cmath>
#include <algorithm>
#include <vector>
#include <queue>
#include <stack>
#include <map>
#include <string>
#include <set>
#define ms(a,b) memset((a),(b),sizeof((a)))
using namespace std;
typedef long long LL;
const double EPS = 1e-8;
const int INF = 2e9;
const LL LNF = 2e18;
const int MAXN = 1e4+10;

struct node
{
    int p, d;
    bool operator<(const node &x)const{
        return p>x.p;
    }
}a[MAXN];
int used[MAXN], n;

int main()
{
    while(scanf("%d", &n)!=EOF)
    {
        memset(used, 0, sizeof(used));
        for(int i = 1; i<=n; i++)
            scanf("%d%d", &a[i].p, &a[i].d);
        sort(a+1, a+1+n);

        int ans = 0;
        for(int i = 1; i<=n; i++)
        {
            for(int j = a[i].d; j>=1; j--)
            if(!used[j])
            {
                used[j] = 1;
                ans += a[i].p;
                break;
            }
        }

        printf("%d\n", ans);
    }

}

 

路径压缩优化：

#include <iostream>
#include <cstdio>
#include <cstring>
#include <cmath>
#include <algorithm>
#include <vector>
#include <queue>
#include <stack>
#include <map>
#include <string>
#include <set>
#define ms(a,b) memset((a),(b),sizeof((a)))
using namespace std;
typedef long long LL;
const double EPS = 1e-8;
const int INF = 2e9;
const LL LNF = 2e18;
const int MAXN = 1e4+10;

struct node
{
    int p, d;
    bool operator<(const node &x)const{
        return p>x.p;
    }
}a[MAXN];
int used[MAXN], fa[MAXN], n;

int find(int x) { return (fa[x]==-1)?x:fa[x]=find(fa[x]); }

int main()
{
    while(scanf("%d", &n)!=EOF)
    {
        memset(used, 0, sizeof(used));
        memset(fa, -1, sizeof(fa));
        for(int i = 1; i<=n; i++)
            scanf("%d%d", &a[i].p, &a[i].d);
        sort(a+1, a+1+n);

        int ans = 0;
        for(int i = 1; i<=n; i++)
        {
            int j = find(a[i].d);
            if(j>0)
            {
                fa[j] = j-1;
                ans += a[i].p;
            }
        }

        printf("%d\n", ans);
    }
}