Codeforces Round #383 (Div. 2) B. Arpa’s obvious problem and Mehrdad’s terrible solution —— 异或

题目链接：http://codeforces.com/contest/742/problem/B

B. Arpa’s obvious problem and Mehrdad’s terrible solution

time limit per test

1 second

memory limit per test

256 megabytes

input

standard input

output

standard output

There are some beautiful girls in Arpa’s land as mentioned before.

Once Arpa came up with an obvious problem:

Given an array and a number x, count the number of pairs of indices i, j (1 ≤ i < j ≤ n) such that 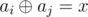, where  is bitwise xoroperation (see notes for explanation).

Immediately, Mehrdad discovered a terrible solution that nobody trusted. Now Arpa needs your help to implement the solution to that problem.

Input

First line contains two integers n and x (1 ≤ n ≤ 105, 0 ≤ x ≤ 105) — the number of elements in the array and the integer x.

Second line contains n integers a1, a2, ..., an (1 ≤ ai ≤ 105) — the elements of the array.

Output

Print a single integer: the answer to the problem.

Examples

input

2 3
1 2

output

1

input

6 1
5 1 2 3 4 1

output

2

Note

In the first sample there is only one pair of i = 1 and j = 2. 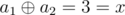 so the answer is 1.

In the second sample the only two pairs are i = 3, j = 4 (since 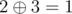) and i = 1, j = 5 (since ).

A bitwise xor takes two bit integers of equal length and performs the logical xor operation on each pair of corresponding bits. The result in each position is 1 if only the first bit is 1 or only the second bit is 1, but will be 0 if both are 0 or both are 1. You can read more about bitwise xor operation here: https://en.wikipedia.org/wiki/Bitwise_operation#XOR.

题解：

1.a^b = c，则：a = b^c，b = a^c。说明：a如果与某个数的异或为c， 那么这个数是唯一的，且可直接求出：b = a^c。

2.c用于记录某个数出现的次数，一边读取数一边操作：假设当前读取的数据为a，则与之对应的数为x^a，则表明a能够与c[x^a]个x^a组成一对，所以 ans += c[x^a]，然后再更新a出现的次数，即c[a]++。

注意之处：

刚开始看到x和a的最大范围为1e5，所以想都不想就把数组也开成1e5，错了一发。

后来发现x^a可能大于1e5，但却不会超过2*1e5，所以应该把数组开成2e5，才不会溢出。

代码如下：

#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
const double eps = 1e-6;
const int INF = 2e9;
const LL LNF = 9e18;
const int mod = 1e9+7;
const int maxn = 1e5+10;

LL n, x;
LL c[maxn<<1]; //!!!!

int main()
{
    cin>>n>>x;
    LL ans = 0, a;
    for(int i = 1; i<=n; i++)
    {
        scanf("%lld",&a);
        ans += c[x^a];
        c[a]++;
    }
    cout<<ans<<endl;
}