Atcoder ARC 061 题解
C - Many Formulas
题意
给出一个长度为10的由数字组成的字符串,你可以把'+'插入到任意位置,将字符串分割,形成一个算式。你有很多分割的方案,现在你需要将所有出现的算式的和相加,然后输出。
例:calc(125) = 125 + (1 + 25) + (12 + 5) + (1 + 2 + 5) = 176
思路
因为长度只有10,爆搜一下。
代码
void dfs(int now, ll tmp_sum, ll sum)
{
if(now == n + 1)
{
res += sum + tmp_sum;
return;
}
dfs(now + 1, tmp_sum * 10 + (s[now] - '0'), sum);
dfs(now + 1, (s[now] - '0'), sum + tmp_sum);
}
int main()
{
cin >> s;
n = s.size();
s = '#' + s;
dfs(1, 0, 0);
cout << res / 2 << '\n'; //要去重所以除2
}
D - Snuke's Coloring
题意
有一个 \(n \times m\) 的矩阵,一开始都是白色,现在要给 \(k\) 个方块染成黑色。我们把这个矩阵分割成 \(3 \times 3\) 的子矩阵,分别输出有多少个子矩阵中含有 \(0,1,2,3,4,\ ... \ ,9\) 个黑方块。
思路
显而易见,计算贡献。我们用每个子矩阵的中心来代表这个子矩阵,那么对一个方格染色,就可以使其上下左右斜方向的子矩阵贡献+1。
代码
const int N = 100005;
int n, m, k;
map<pair<int, int>, int> mp;
int x[N], y[N];
ll res[10];
int main()
{
cin >> n >> m >> k;
res[0] = 1ll * (n - 2) * (m - 2);
for(int i = 1; i <= k; i ++)
{
int x, y;
cin >> x >> y;
for(int i = max(2, x - 1); i <= min(n - 1, x + 1); i ++)
for(int j = max(2, y - 1); j <= min(m - 1, y + 1); j ++)
mp[make_pair(i, j)] ++;
}
for(auto it : mp)
res[it.second] ++, res[0] --;
for(int i = 0; i <= 9; i ++)
cout << res[i] << '\n';
}
E - Snuke's Subway Trip
题意
给出一张无向图,有 \(n\) 个点和 \(m\) 条边组成。每条边有一个类型,若是在路途中边的类型发生变化,那么需要花费1点代价。从起点 \(1\) 开始第一步也是需要花费 \(1\) 点代价的。请问从起点 \(1\) 走到终点 \(n\) 的最小代价是多少。
思路
拆边建图。我们把每个边拆成两个点,比如(2 -> 3, 1),意思是从2到3连一条类型为1的边,关于这条边,我们一共有四个点,分别是2,3,(2, 1),(3, 1)。建图成这样,在这个上跑最短路然后把总费用除二。下面有正确性示例:
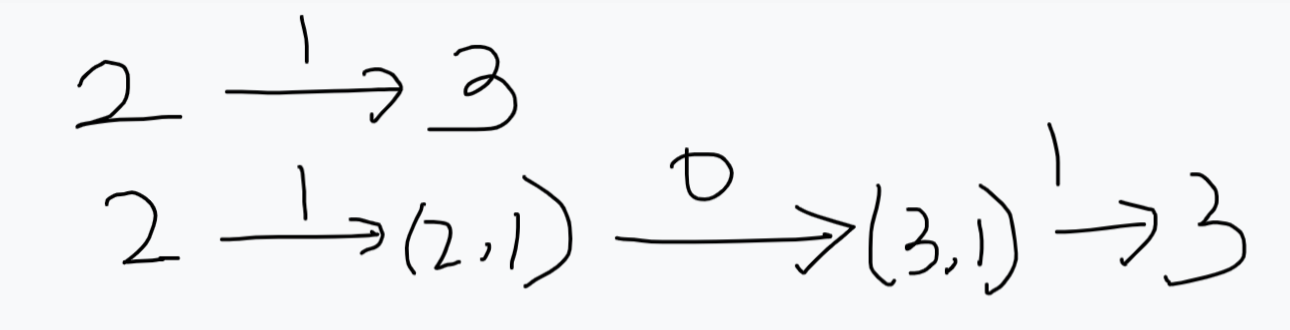
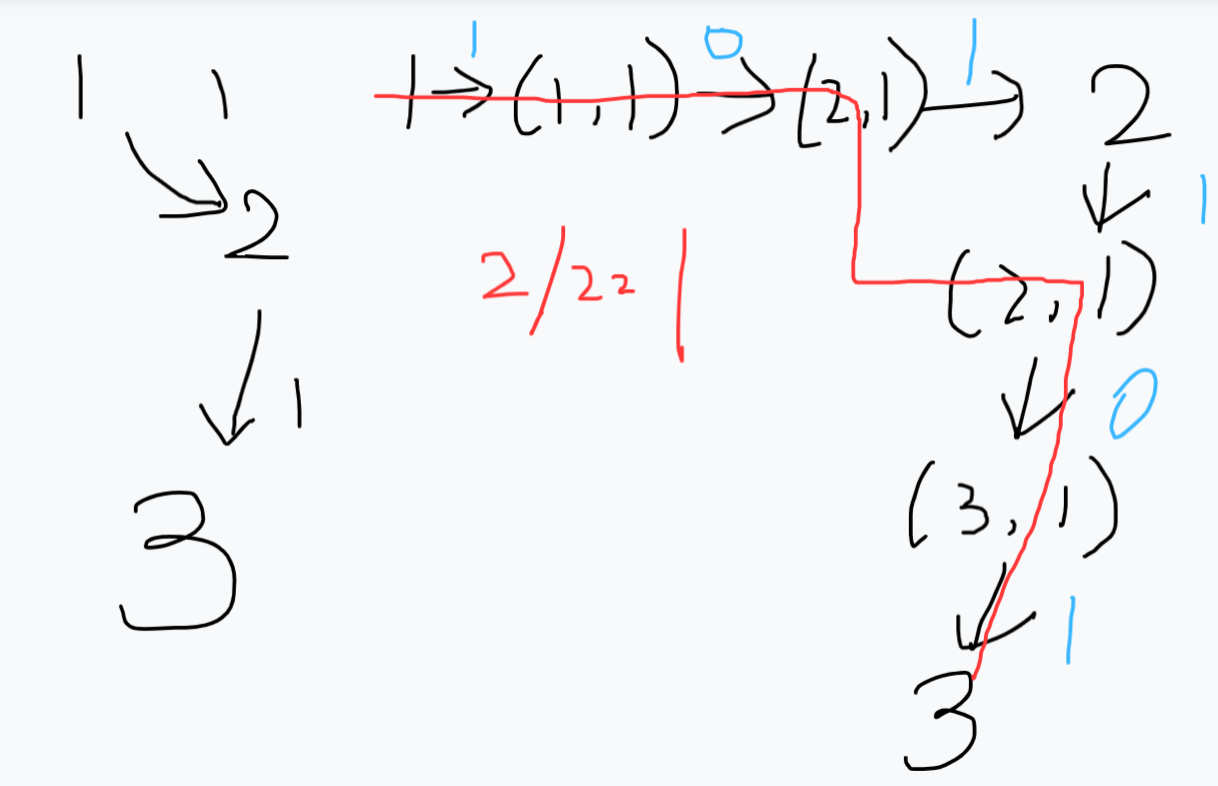
代码
const int N = 1000005;
int n, m;
vector<PII> g[N];
int dis[N], vis[N];
map<PII, int> mp;
int num = 100005;
int open_point(int x, int y)
{
auto pr = make_pair(x, y);
if(!mp.count(pr))
mp[pr] = ++ num;
return mp[pr];
}
void Dji(int st)
{
memset(dis, 0x3f, sizeof dis);
dis[st] = 0;
priority_queue<PII, vector<PII>, greater<PII> > q;
q.push(make_pair(0, st));
while(q.size())
{
int u = q.top().second;
q.pop();
if(vis[u]) continue;
vis[u] = 1;
for(auto [v, w] : g[u])
{
if(dis[v] > dis[u] + w)
{
dis[v] = dis[u] + w;
q.push(make_pair(dis[v], v));
}
}
}
}
int main()
{
cin >> n >> m;
while(m --)
{
int x, y, c;
cin >> x >> y >> c;
int d1 = open_point(x, c);
int d2 = open_point(y, c);
g[x].push_back(make_pair(d1, 1));
g[d1].push_back(make_pair(x, 1));
g[y].push_back(make_pair(d2, 1));
g[d2].push_back(make_pair(y, 1));
g[d1].push_back(make_pair(d2, 0));
g[d2].push_back(make_pair(d1, 0));
}
Dji(1);
int res = dis[n];
if(res == inf)
res = -2;
cout << res / 2 << '\n';
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号