【数值分析】欧拉方法、梯形方法与预估-校正Euler公式 Python实现代码
1 # -*- coding: utf-8 -*- 2 """ 3 Created on Wed Mar 25 09:49:28 2020 4 5 @author: dengjiepython 隐式欧拉方法 6 """ 7 import math 8 import numpy as np 9 import matplotlib.pyplot as plt 10 11 12 def fxy(x,y): 13 f_xy = -y + x + 1 14 # 真解为 math.exp(float(-self.x))+self.x 15 return f_xy 16 17 18 #定义一个欧拉算法的类 19 class Euler: 20 21 def __init__(self, h, y0): 22 self.y_list = [] 23 self.h = h 24 self.y = y0 25 self.n = 1/self.h 26 self.x = 0 27 self.x_list = np.linspace(0, 1, self.n + 1, dtype=float) 28 self.euler() 29 self.trapezoid() 30 self.modified_euler() 31 32 33 def euler(self): # 定义Euler算法的过程 34 for i in range(int(self.n + 1)): 35 f_xy = fxy(self.x,self.y) 36 z1 = self.y 37 self.y += self.h * f_xy 38 if len(Euler_y_list)<int(self.n + 1): 39 Euler_y_list.append('%.10f'%self.y) 40 err_euler.append(abs(z1-(math.exp(float(-self.x))+self.x))) 41 self.x += self.h 42 self.Euler_y_list = Euler_y_list 43 self.err_euler = err_euler 44 self.x = 0 45 self.y = y0 46 return self.x_list, self.Euler_y_list, self.err_euler 47 48 49 def trapezoid(self):#梯形方法 50 for i in range(int(self.n + 1)): 51 k=1 52 x_next = self.x 53 y_next = self.y+self.h*fxy(x_next,self.y) 54 z1 = self.y 55 err_trap.append(abs(z1-(math.exp(float(-self.x))+self.x))) 56 while k <= 10: 57 y_next = self.y + 0.5*self.h*(fxy(x_next,self.y)+fxy(x_next+self.h,y_next)) 58 k+=1 59 self.y = y_next 60 self.x += self.h 61 if len(trapezoid_list)<int(self.n + 1): 62 trapezoid_list.append(self.y) 63 self.trapezoid_list = trapezoid_list 64 self.err_trap = err_trap 65 self.x = 0 66 self.y = y0 67 return self.x_list, self.trapezoid_list, self.err_trap 68 69 70 def modified_euler(self):#预估-校正欧拉方法 71 for i in range(int(self.n + 1)): 72 f_xy = fxy(self.x,self.y) 73 y_esti = self.y + self.h * f_xy 74 z1 = self.y 75 err_modi.append(abs(z1-(math.exp(float(-self.x))+self.x))) 76 self.x += self.h 77 self.y += 0.5*self.h*(f_xy+fxy(self.x,y_esti)) 78 if len(modified_euler_list)<int(self.n + 1): 79 modified_euler_list.append('%.10f'%self.y) 80 self.modified_euler_list = modified_euler_list 81 self.err_modi = err_modi 82 self.x = 0 83 self.y = y0 84 return self.x_list, self.modified_euler_list, self.err_modi 85 86 87 def view_result(self): 88 self.Euler_y_list = [float(item) for item in self.Euler_y_list ] 89 self.trapezoid_list = [float(item) for item in self.trapezoid_list ] 90 self.modified_euler_list = [float(item) for item in self.modified_euler_list ] 91 self.err_euler = [float(item) for item in self.err_euler ] 92 self.err_trap = [float(item) for item in self.err_trap ] 93 self.err_modi = [float(item) for item in self.err_modi ] 94 plt.style.use('ggplot') 95 plt.figure(num=1,figsize=(8,4)) 96 plt.title('Result of $ df = -y+x+1$') 97 plt.xlabel('x') 98 plt.ylabel('y') 99 100 plt.ylim() 101 plt.plot(self.x_list, self.Euler_y_list, 'c*-', label='Euler Method', linewidth=2) 102 plt.plot(self.x_list, self.trapezoid_list, 'ro-', label='Trapezoid Method', linewidth=2) 103 plt.plot(self.x_list, self.modified_euler_list, 'g^-', label='Modified_Euler Method', linewidth=1) 104 105 plt.legend(loc='best') 106 plt.savefig('fig_value.png', dpi=600) 107 plt.show() 108 109 plt.figure(num=1,figsize=(8,4)) 110 plt.title('Error of three methods $ df = -y+x+1$') 111 plt.xlabel('x') 112 plt.ylabel('error') 113 plt.ylim() 114 plt.plot(self.x_list, self.err_euler, 'c*-', label='Euler Method', linewidth=2) 115 plt.plot(self.x_list, self.err_trap, 'ro-', label='Trapezoid Method', linewidth=2) 116 plt.plot(self.x_list, self.err_modi, 'g^-', label='Modified_Euler Method', linewidth=1) 117 118 plt.legend(loc='best') 119 plt.savefig('fig_err.png', dpi=600) 120 plt.show() 121 122 123 if __name__ == "__main__": 124 err_euler=[] 125 err_trap = [] 126 err_modi = [] 127 y0 = 1 128 modified_euler_list = [y0] 129 Euler_y_list = [y0] 130 trapezoid_list = [y0] 131 132 res = Euler(h=0.1,y0=1) 133 res.view_result() 134
使用欧拉方法、梯形方法与预估-校正Euler公式对以下常微分方程进行求解:
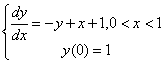
代码如上所示。
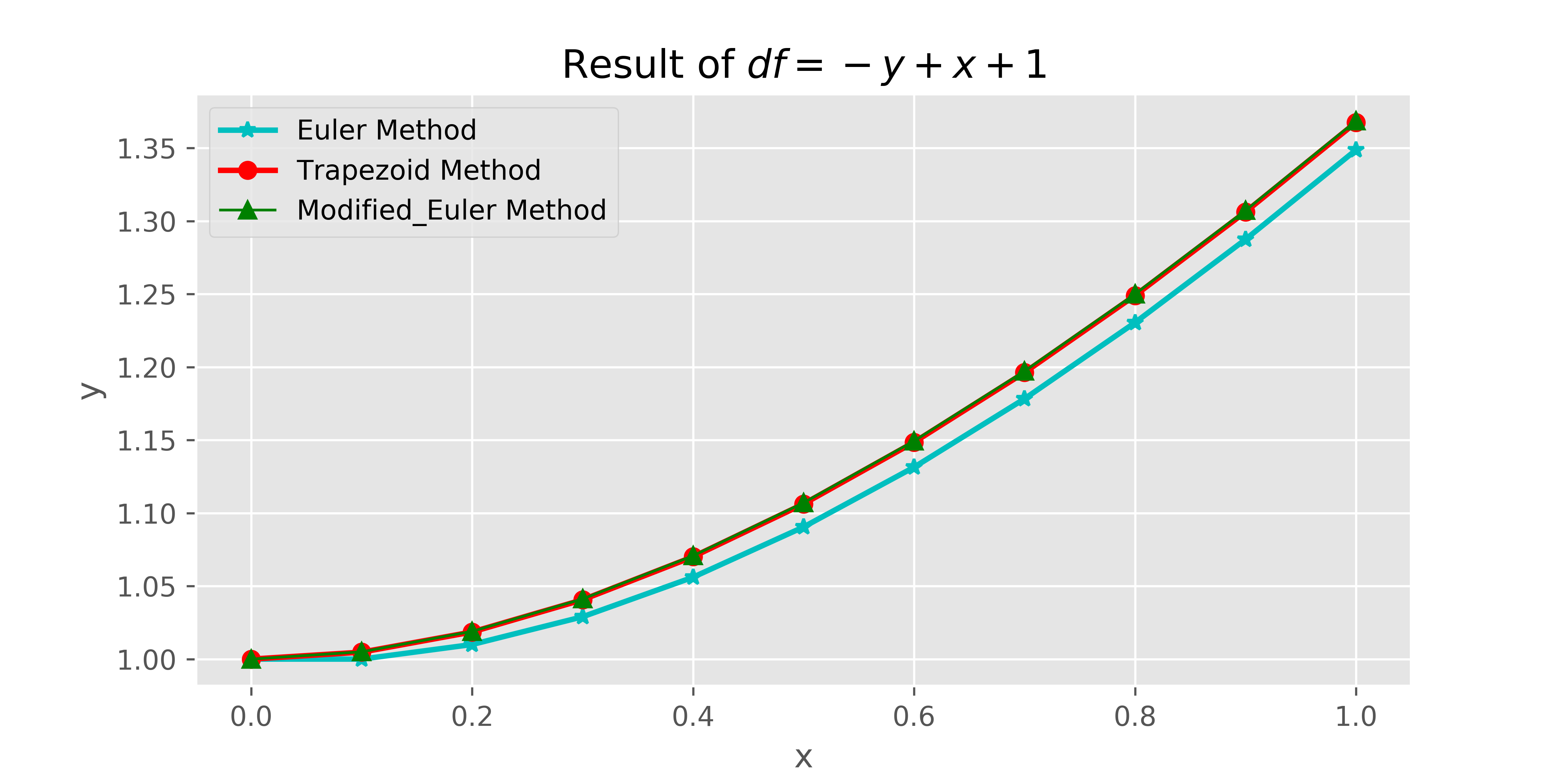
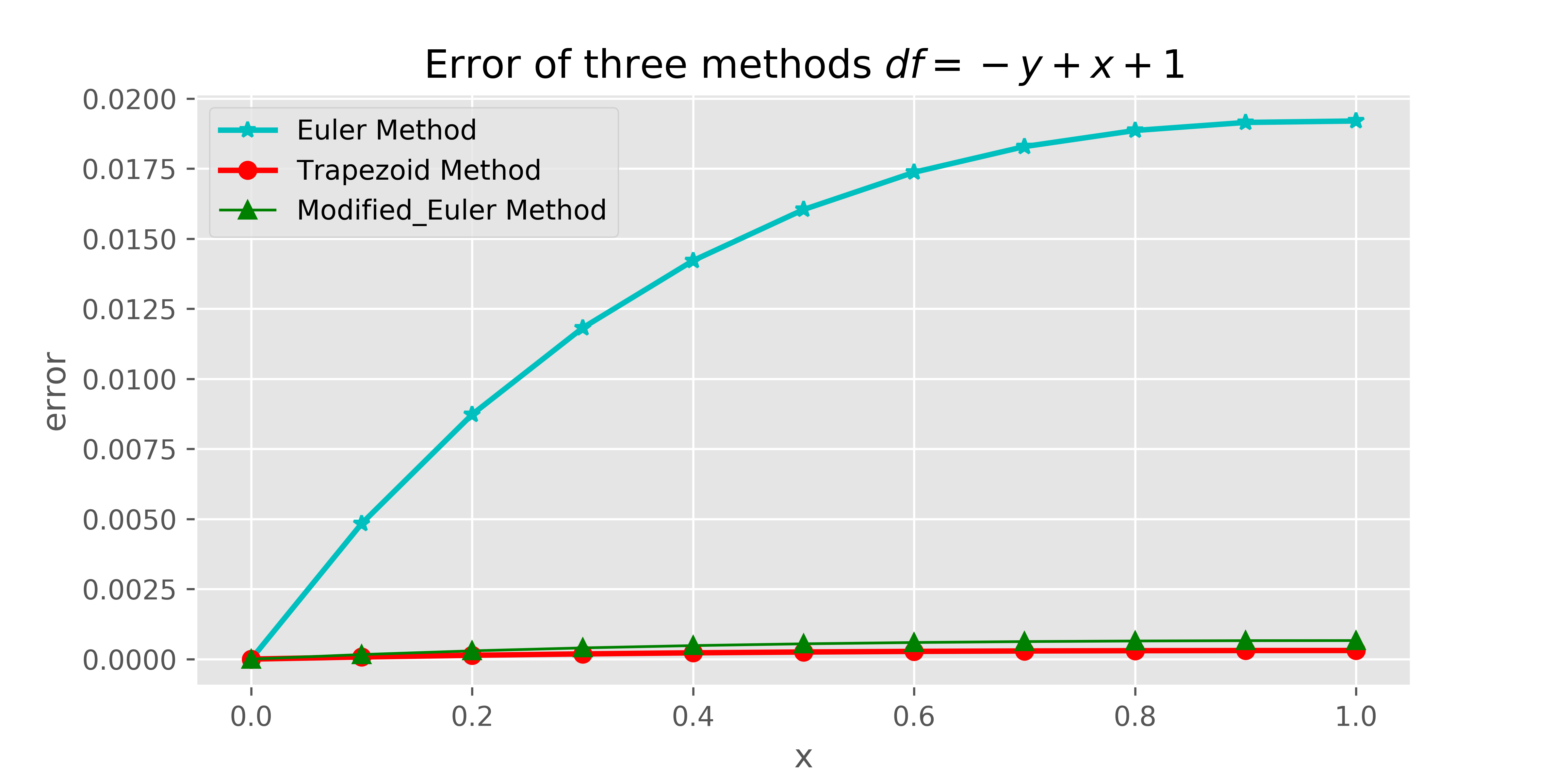
参考博客:
http://www.pynumerical.com/archives/32/
https://blog.csdn.net/u013007900/article/details/45317927
https://blog.csdn.net/qq_35240640/article/details/89445826
https://wenku.baidu.com/view/d5d2763467ec102de2bd898a.html?sxts=1585100623950
局部截断误差与整体截断误差:
https://wenku.baidu.com/view/fe80a729eef9aef8941ea76e58fafab069dc44b7.html
微分方程的应用场景:
https://max.book118.com/html/2018/1014/6152143022001223.shtm
https://wenku.baidu.com/view/6f80cbd010661ed9ac51f390.html
http://www.fx361.com/page/2018/0306/4990403.shtml
https://www.ixueshu.com/document/e4859208ffe87b81bd1fc1c567b8ba29318947a18e7f9386.html
https://www.ixueshu.com/document/e1ee191d9172355e318947a18e7f9386.html



