tensorflow学习笔记(4)-学习率

 

　　　　　　　　　　　　　　tensorflow学习笔记(4)-学习率

---

 

首先学习率如下图

所以在实际运用中我们会使用指数衰减的学习率

在tf中有这样一个函数

tf.train.exponential_decay(learning_rate, global_step, decay_steps, decay_rate, staircase=False, name=None)

首先看下它的数学表达式：decayed_learing_rate=learing_rate*decay_rate^(gloabl_steps/decay_steps)

　　如图

 

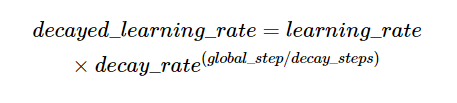
1. 第一个参数是学习率，
2. /第二个参数是用来计算训练论数的，每次加一
3. 第三个参数通常设为常数
4. 第四个参数是学习率下降的倍率
5. 第五个参数设为True则指数部分会采用取整的方式

 

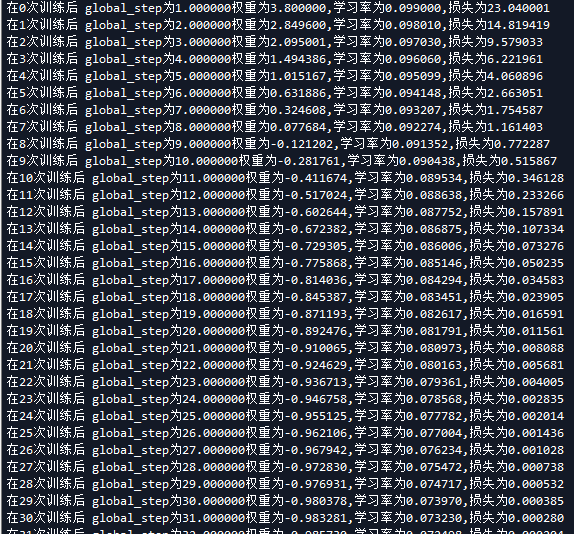
# -*- coding: utf-8 -*-
"""
Created on Sun May 27 11:19:46 2018

@author: Administrator
"""
#设算是函数loss=(w+1)^2令w初始值为常熟10，反向传播求最优w，求最小loss对应的w的值
#使用指数衰减的学习率，在迭代初期有比较搞的下降速度，可以在比较小的训练轮数下更有收敛度

import tensorflow as tf
LEARNING_RATE_BASE=0.1 #最初学习率
LEARNING_RATE_DECAY=0.99#学习率衰减
LEARNING_RATE_STEP=1#喂入多少伦BATCH_SIZE后更新一次学习率，一般威威总样本数/BATCH_SIZE

#运行了几轮BATCH_SIZE的计数器，初值给0，设为不被训练
global_step=tf.Variable(0,trainable=False)
#定义指数下降学习率
learning_rate=tf.train.exponential_decay(LEARNING_RATE_BASE,global_step,
                                        LEARNING_RATE_STEP,LEARNING_RATE_DECAY
                                        ,staircase=True)
#定义待优化参数，初始值10
w=tf.Variable(tf.constant(5,dtype=tf.float32))
#定义损失函数
loss=tf.square(w+1)
#定义反向传播方法
train_step=tf.train.GradientDescentOptimizer(learning_rate).minimize(
        loss,global_step=global_step)
#生成会话，训练40论
with tf.Session() as sess:
    init_op=tf.global_variables_initializer()
    sess.run(init_op)
    for i in range(40):
        sess.run(train_step)
        #更新学习速率
        learning_rate_val=sess.run(learning_rate)
        global_step_val=sess.run(global_step)
        w_val=sess.run(w)
        loss_val=sess.run(loss)
        print("在%s次训练后 global_step为%f权重为%f,学习率为%f,损失为%f"%(i,
                                                          global_step_val,
                                                          w_val,learning_rate_val,
                                                          loss_val))

运行结果如下，我们也可以改变学习率更改的速率或者其他参数来看对损失率的影响。