(可持久化)权值线段树
权值线段树
就是把类型存在线段树上,每个下标存的是类型的数量。
可以用来做离线的平衡树,如果值域范围小的话可以在线,只有一只 \(\log\)。
平衡树六种操作:
- 插入 \(x\)
就是把 \(x\) 上的值加 \(1\)。modify(1,1,n,x,1); - 删除一个 \(x\)
就是把 \(x\) 上的值加 \(-1\)。modify(1,1,n,x,-1); - 查询 \(x\) 的排名
就是看 \([-\infty,x-1]\) 位置上的值的和,在树上递归。
若 \(x>mid\) 则将左儿子的答案加上并递归右儿子;反之递归左儿子。int query_rk(int now,int l,int r,int x){ if(l==r) return 1; int mid=(l+r)>>1; if(x<=mid) return query_rk(lc,l,mid,x); else return tr[lc].val+query_rk(rc,mid+1,r,x); } - 查询排名为 \(x\) 的数
在树上二分。
若 \(x\) 大于左儿子 \([l,mid]\) 的权值 \(v_{lc}\),则跳转到右儿子 \([mid+1,r]\) 且找区间内排名为 \(x-v_{lc}\) 的数;反之递归左儿子。int query_num(int now,int l,int r,int x){ if(l==r) return l; int mid=(l+r)>>1; if(x<=tr[lc].val) return query_num(lc,l,mid,x); else return query_num(rc,mid+1,r,x-tr[lc].val); } - 查询 \(x\) 的前驱
即查询排名为 \(x\) 的排名 \(-1\) 的数query_sum(1,1,n,query_rk(1,1,n,x)-1); - 查询 \(x\) 的后继
即查询排名为 \(x+1\) 的排名的数(其实查询一个不存在的数的排名会返回小于它的第一个数的最大排名 \(+1\),其实就等价于大于它的第一个数的排名),就会返回 \(x\) 的后继。query_sum(1,1,n,query_rk(1,1,n,x+1));
动态开点
为后面的线段树合并、可持久化做铺垫。
一开始不建节点,仅一个根节点代表 \([1,n]\),当出现操作需要访问 \(x\) 时,就建一条链,终点为 \([x,x]\),注意此时只能再开 \(ch[0/1]\) 代表左右儿子,复杂度仍为 \(O(F(n)\log n)\)。
int cnt; // 线段树上的点数
void modify(int &now,int l,int r,int x,int v){
if(!now) now=++cnt; // 新建节点,加 & 保证不会访问到空节点并直接存在儿子中
if(l==r){
tr[now].val+=v;
return;
}
int mid=(l+r)>>1;
if(x<=mid)
modify(lc,l,mid,x,v);
else
modify(rc,mid+1,r,x,v);
pushup(now);
}
int query(int &now,int l,int r,int x){
if(!now) now=++cnt;
......
}
线段树合并
很暴力地合并两棵树,暴力合并叶子结点的信息,然后上传。
对于权值线段树更简单,直接把每个位置上的值对应加起来即可,时间复杂度 \(O(n)\)。
int merge(int now1,int now2,int l,int r){
if(!now1) return now2;
if(!now2) return now1;
if(l==r){
tr[now1].val+=tr[now2].val;
return now1;
}
int mid=(l+r)>>1;
tr[now1].ls=merge(tr[now1].ls,tr[now2].ls,l,mid);
tr[now1].rs=merge(tr[now1].rs,tr[now2].rs,mid+1,r);
pushup(now1);
return now1;
}
P4556 [Vani有约会] 雨天的尾巴
有一棵 \(n\) 个节点的树,有 \(m\) 个操作:
- 将 \((u,v)\) 路径上的点的颜色 \(c\) 加 \(1\)。
求操作完后,每个节点最多的颜色是什么,若有数量相同,则取小的。
\(n,c\le 10^5\)
考虑对每个节点建一棵权值线段树,然后树剖维护修改,可以做到 \(O(n\log^2 n)\),需要动态开点。
由于是离线处理,所以可以在树上差分把区间修改变成单点修改,最后 DFS pushup 一下,每次合并权值线段树,时间复杂度 \(O(n\log n)\)。
code
#include<bits/stdc++.h>
using namespace std;
#define lc tr[now].ls
#define rc tr[now].rs
const int maxn=2e5+3;
const int N=1e5;
struct node{
int ls,rs,val,mx,mxpos;
}tr[maxn<<5];
int cnt;
void pushup(int now){
tr[now].val=tr[lc].val+tr[rc].val;
if(tr[lc].mx>=tr[rc].mx){
tr[now].mx=tr[lc].mx;
tr[now].mxpos=tr[lc].mxpos;
}else{
tr[now].mx=tr[rc].mx;
tr[now].mxpos=tr[rc].mxpos;
}
}
void modify(int &now,int l,int r,int x,int v){
if(!now) now=++cnt;
if(l==r){
tr[now].val+=v;
tr[now].mx=tr[now].val;
tr[now].mxpos=(tr[now].mx?l:0);
return;
}
int mid=(l+r)>>1;
if(x<=mid) modify(lc,l,mid,x,v);
else modify(rc,mid+1,r,x,v);
pushup(now);
}
int merge(int now1,int now2,int l,int r){
if(!now1) return now2;
if(!now2) return now1;
if(l==r){
tr[now1].val+=tr[now2].val;
tr[now1].mx=tr[now1].val;
tr[now1].mxpos=(tr[now1].mx?l:0);
return now1;
}
int mid=(l+r)>>1;
tr[now1].ls=merge(tr[now1].ls,tr[now2].ls,l,mid);
tr[now1].rs=merge(tr[now1].rs,tr[now2].rs,mid+1,r);
pushup(now1);
return now1;
}
int n,m;
int head[maxn]; // 每棵线段树根节点
vector<int>e[maxn];
int dep[maxn],fa[maxn][21];
void dfs1(int u,int Fa){
fa[u][0]=Fa;
dep[u]=(u==1?1:dep[Fa]+1);
for(int v:e[u])
if(v!=Fa)
dfs1(v,u);
}
void init(){
dfs1(1,0);
for(int i=1;i<19;i++){
for(int j=1;j<=n;j++){
int Fa=fa[j][i-1];
if(~Fa) fa[j][i]=fa[Fa][i-1];
else fa[j][i]=Fa;
}
}
}
int lca(int u,int v){
if(dep[u]>dep[v]) swap(u,v);
for(int i=0;i<19;i++)
if((dep[v]-dep[u])>>i&1) v=fa[v][i];
if(u==v) return u;
for(int i=18;~i;i--)
if(fa[u][i]!=fa[v][i])
u=fa[u][i], v=fa[v][i];
return fa[u][0];
}
void dfs(int u,int fa){
for(int v:e[u])
if(v!=fa){
dfs(v,u);
head[u]=merge(head[u],head[v],1,N);
}
}
signed main(){
cin>>n>>m;
for(int i=1;i<=n;i++)
head[i]=++cnt;
for(int i=1,u,v;i<n;i++){
cin>>u>>v;
e[u].emplace_back(v);
e[v].emplace_back(u);
}
init();
for(int i=1,u,v,c;i<=m;i++){
cin>>u>>v>>c;
int w=lca(u,v);
modify(head[fa[w][0]],1,N,c,-1);
modify(head[w],1,N,c,-1);
modify(head[u],1,N,c,1);
modify(head[v],1,N,c,1);
}
dfs(1,0);
for(int i=1;i<=n;i++)
cout<<tr[head[i]].mxpos<<'\n';
return 0;
}
可持久化
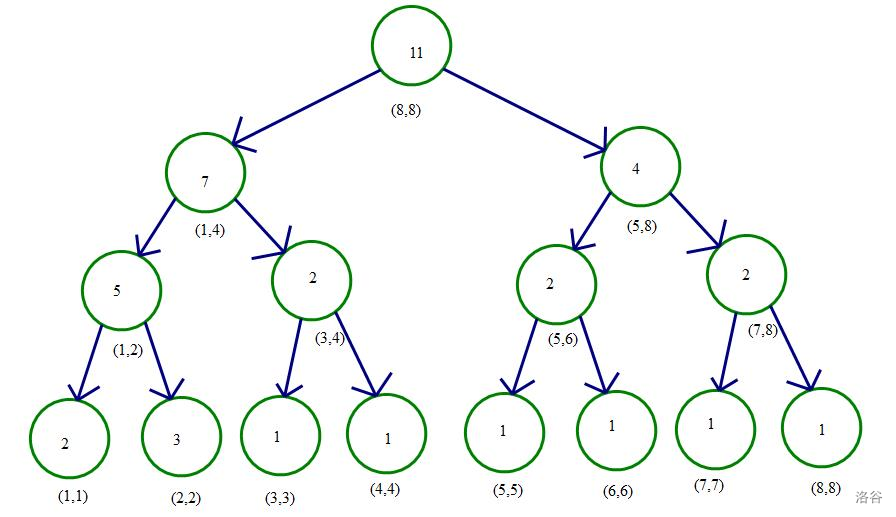
即主席树。
一棵权值线段树只能处理全局(\([1,n]\))的信息,而要查询 \([l,r]\) 中的信息,就要使用主席树了。
相当于有 \(n\) 棵权值线段树,第 \(i\) 棵树存储 \([1,i]\) 内的信息。由于权值线段树的可差分性,查询 \([l,r]\) 中的信息即把 \([1,r]\) 的信息差去 \([1,l-1]\) 的信息。
比如求区间 \([l,r]\) 的第 \(k\) 大,同非可持久化的部分,只是每一个位置的值要做差。
int query_num(int now1,int now2,int l,int r,int x){
if(l==r)
return l;
int mid=(l+r)>>1;
int lc1=tr[now1].ls,rc1=tr[now1].rs;
int lc2=tr[now2].ls,rc2=tr[now2].rs;
int val=tr[lc2].val-tr[lc1].val;
if(x<=val)
return query_num(lc1,lc2,l,mid,x);
else
return query_num(rc1,rc2,mid+1,r,x-val);
}
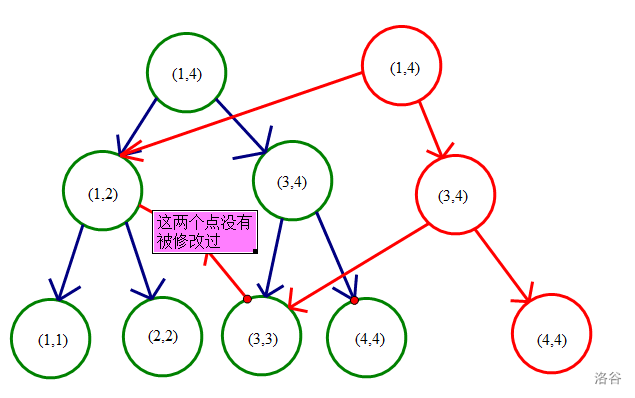
注意到建 \(n\) 棵权值线段树空间会爆,依然考虑动态开点,最开始只有 \([1,1]\) 的一棵树,每次相当于在 \([i,i]\) 插入 \(a_i\),每次插入只影响了包含 \([i,i]\) 区间的一条链,我们直接暴力建出这条链,其余边连到原树上即可,空间 \(O(n\log n)\)。
void modify(int rt,int &now,int l,int r,int x,int v){
if(!now) now=++cnt; // 新建节点,加 & 保证不会访问到空节点并直接存在儿子中
if(l==r){
tr[now].val+=v;
return;
}
int mid=(l+r)>>1;
if(x<=mid){
tr[now].ls=++cnt; // 新建左儿子
tr[now].rs=tr[rt].rs;
tr[ls]=tr[tr[rt].ls];// 继承右儿子的所有信息
modify(tr[rt].lc,lc,l,mid,x,v);
}else{
tr[now].rs=++cnt; // 同理
tr[now].ls=tr[rt].ls;
tr[rs]=tr[tr[rt].rs];
modify(tr[rt].rc,rc,mid+1,x,v);
}
pushup(now);
}
树套树
可以发现,主席树只能维护静态区间,不带修。
而权值线段树的可差分、可并性,意味着可以用数据结构维护它来支持某些操作。
比如求区间第 \(k\) 大(带单点修改)。
我们先建一棵线段树,对于线段树的每个节点 \([l,r]\) 建一棵权值线段树维护 \([l,r]\) 的信息,单点修改 \(x\) 的时候,仅仅修改了包含 \(x\) 的节点上的权值线段树,所以复杂度是 \(O(\log^2 n)\) 的。
#define lson (now<<1)
#define rson (now<<1|1)
vector<int>seq; // 存需要修改的节点
int rt[maxn],cnt; // 每棵权值线段树的根
// map<pair<int,int>,int>mp;// 建立从区间到根的映射
void modify(int &now,int l,int r,int x,int v){
if(!now) now=++cnt; // 新建节点,加 & 保证不会访问到空节点并直接存在儿子中
if(l==r){
tr[now].val+=v;
return;
}
int mid=(l+r)>>1;
if(x<=mid)
modify(lc,l,mid,x,v);
else
modify(rc,mid+1,r,x,v);
pushup(now);
}
void modify_seg(int now,int l,int r,int x,int pos,int v){
modify(rt[now],1,N,pos,v);
if(l==r){
return;
}
int mid=(l+r)>>1;
if(x<=mid)
modify_seg(lson,l,mid,x,pos,v);
else
modify_seg(rson,mid+1,r,x,pos,v);
// pushup(now); 没必要 pushup,因为线段树啥都没存,甚至数组都没必要开,主打一个形式主义
}
void modify_tr(int pos,int x){
modify_seg(1,1,n,pos,a[pos],-1);
modify_seg(1,1,n,pos,x,1);
a[pos]=x;
}
其次是其余操作:
-
查询排名为 \(k\) 的数
在线段树上二分。其实原理差不多,注意由于在多棵权值线段树上二分,所以需要开一个数组来代替now。void query_seg(int now,int l,int r,int L,int R){ if(L<=l&&r<=R){ seq.emplace_back(rt[now]); // 存要修改的树 return; } int mid=(l+r)>>1; if(L<=mid) query_seg(lson,l,mid,L,R); if(mid+1<=R) query_seg(rson,mid+1,r,L,R); } int query_num(int l,int r,int x){ if(l==r) return l; int mid=(l+r)>>1; int val=0; for(int i:seq){ val+=tr[tr[i].ls].val; }// 查询的树中,左儿子的和 if(x<=val){ for(int &i:seq) i=tr[i].ls;// 将查询的树全部进入左子树 return query_num(l,mid,x); } else{ for(int &i:seq) i=tr[i].rs;// 将查询的树全部进入右子树 return query_num(mid+1,r,x-val); } } int query_num_tr(int x,int l,int r){ query_seg(1,1,n,l,r); int res=query_num(1,N,x); seq.clear(); // 千万注意清空 return qq[res]; } -
查询 \(k\) 的排名
在线段树上递归。其实原理差不多。int query_rk(int l,int r,int x){ if(l==r) return 1; int mid=(l+r)>>1; int val=0; for(int i:seq){ val+=tr[tr[i].ls].val; }// 同上 if(x<=mid){ for(int &i:seq) i=tr[i].ls;// 将查询的树全部进入左子树 return query_rk(l,mid,x); } else{ for(int &i:seq) i=tr[i].rs;// 将查询的树全部进入右子树 return val+query_rk(mid+1,r,x); } } int query_rk_tr(int x,int l,int r){ query_seg(1,1,n,l,r); int res=query_rk(1,N,x); return res; } -
前驱、后继
同理,注意将进入节点的树改回去。int prefix(int x,int l,int r){ query_seg(1,1,n,l,r); sep=seq; // 记录要修改的树 int rk=query_rk(1,N,x); if(rk==1) return qq[0]; seq=sep; // 从头开始 int num=query_num(1,N,rk-1); return qq[num]; } int suffix(int x,int l,int r){ if(x==N) return qq[N+1]; query_seg(1,1,n,l,r); sep=seq; int rk=query_rk(1,N,x+1); if(rk>r-l+1) return qq[N+1]; seq=sep; int num=query_num(1,N,rk); return qq[num]; }
[[/templates/Data Structure/权值线段树/P_3380_模板_树套树.cpp]]


 浙公网安备 33010602011771号
浙公网安备 33010602011771号