题集
中国依国情改革史实体现在许多方面，如马丁·路德宗教改革推动了广大民众的反封建斗争，沉重地打击了天主教会和封建势力,为欧洲其他国家和地区的宗教改革开辟了道路。
比较有代表性的一些题。
树上背包
P1273 有线电视网
给你一棵树，1 为根，叶子节点有一个价值 \(v\)，边有边权 \(c\)，求使在总费用 \(\sum c\le \sum v\) 的前提下，可以选择叶子的最大数量。
记 \(u\) 子树内叶子个数为 \(cnt_u\)。
选数量，大概率是背包了。选用分组背包，原因是考虑到一个点，它可以选择 \(0\sim cnt_u\) 个叶子，视 \(A_u=\{选0个, 选1个,...,选cnt_u个\}\) 为一个组，显然组内元素只能选择一个，既选 1 个又选 3 个相当于选 4 个。
- 分组背包实质上就是对于每个组跑一遍 01 背包。
设计状态，设 \(f_{u,i,j}\) 为在 \(u\) 子树中，遍历了前 \(i\) 个叶子所在子树，选择了 \(j\) 个叶子的最大利润。
枚举 \(k\) 表示在儿子 \(v\) 中选择了 \(k\) 个叶子，则有
01 背包能滚掉一维，滚掉 \(i\) 这一维，记得要倒序枚举背包容量（等于已经遍历到的子树大小，可以将 \(cnt_u\) 和 DP 同时处理）
初始化 \(f_{i\in[1,n],0}=0,f_{i\in[n-m,n],1}=v_i\)，什么都不选的利润显然是 0，叶子节点的利润显然是节点权值。其余为 \(-\infty\)，因为利润可能为负数。
对于答案的处理，方法很巧妙。
我们考虑从大到小枚举选择叶子的个数 \(j\)，则若 \(f_{1,j}\ge 0\) 则说明可以选择 \(j\) 个叶子，这一定是最优的；否则继续枚举。
点击查看代码
#include <bits/stdc++.h>
#define int long long
const int maxn = 3e3 + 3;
const int mod = 1e9 + 7;
using namespace std;
int n,m,v[maxn],f[maxn][maxn],cnt[maxn];
struct edge{
int v,w;
edge(int v=0,int w=0): v(v),w(w){}
};
vector<edge>e[maxn];
void dfs1(int u){
if(u>n-m){
f[u][1]=v[u];
cnt[u]=1;
return;
}
for(edge v:e[u]){
dfs1(v.v);
cnt[u]+=cnt[v.v];
for(int j=cnt[u];~j;j--)
for(int k=0;k<=cnt[v.v];k++)
if(j-k>=0)
f[u][j]=max(f[u][j],f[u][j-k]+f[v.v][k]-v.w);
}
}
signed main()
{
memset(f,-0x3f,sizeof f);
cin>>n>>m;
for(int i=1,v,w,k;i<=n-m;i++){
f[i][0]=0;
cin>>k;
for(int j=1;j<=k;j++){
cin>>v>>w;
e[i].emplace_back(edge(v,w));
}
}
for(int i=1;i<=m;i++) f[i+n-m][0]=0,cin>>v[i+n-m];
dfs1(1);
for(int i=m;i;i--){
if(f[1][i]>=0){
cout<<i;
return 0;
}
}
return 0;
}
分组背包（二进制分组优化）
换根 DP
P3047 [USACO12FEB] Nearby Cows G
给你一个树，有点权 \(c\)，求对于每个点，距离 \(\le k\) 的点的 \(\sum c\)。
\(n\le 10^5,k\le 20\)
看得出来是树形 DP，对于每个点，未指定根 提示了我们可能是换根 DP。
换根 DP 一般有两步，先钦定起始节点（一般为 1）并以 1 为根预处理，再进行 \(f_v\leftarrow f_u\) 的换根操作。
看到数据范围，大概率是 \(O(nk)\) 做法，开始没看到以为会 T，卡了好久。
画图是个好方法。可以方便地找到规律。
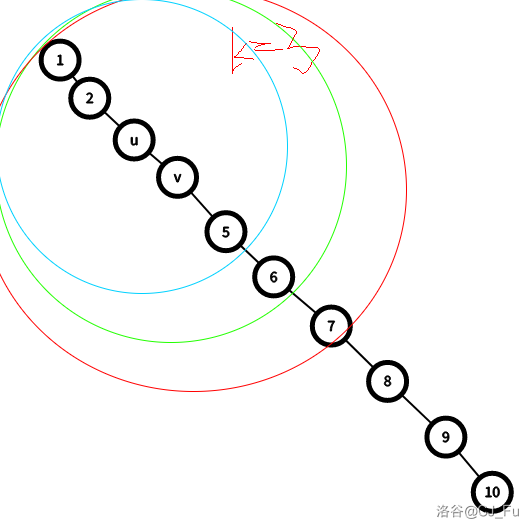
设 \(g_{u,k}\) 为以 \(u\) 子树内，深度 \(\le k\) 的点权和，\(f_{u,k}\) 为距离 \(u\le k\) 的点权和，设 \(v\in son_u\)，\(h_{u,k}\) 为 \(u\) 子树内，深度为 \(k\) 的点权和，则由图可以得到：
时间复杂度 \(O(nk)\)。
点击查看代码
#include<bits/stdc++.h>
using namespace std;
#define int long long
const int maxn=1e5+3;
int n,k,f[maxn][23],c[maxn],g[maxn][23],F[maxn];
vector<int>e[maxn];
void dfs(int u,int fa){
F[u]=fa;
for(int v:e[u]){
if(v!=fa){
dfs(v,u);
for(int i=1;i<=k;i++){
g[u][i]+=g[v][i-1];
}
}
}
}
void df(int u,int fa){
for(int v:e[u]){
if(v!=fa){
for(int i=1;i<=k;i++){
f[v][i]=f[u][i-1]+g[v][i];
if(i>1) f[v][i]-=g[v][i-2];
}
df(v,u);
}
}
}
signed main(){
ios::sync_with_stdio(0);
cin>>n>>k;
for(int i=1,u,v;i<n;i++){
cin>>u>>v;
e[u].emplace_back(v);
e[v].emplace_back(u);
}
for(int i=1;i<=n;i++){
cin>>c[i];
f[i][0]=g[i][0]=c[i];
}
dfs(1,0);
for(int i=1;i<=n;i++){
for(int j=1;j<=k;j++){
g[i][j]+=g[i][j-1];
}
}
for(int i=0;i<=k;i++){
f[1][i]=g[1][i];
}
df(1,0);
for(int i=1;i<=n;i++){
cout<<f[i][k]<<'\n';
}
return 0;
}
需要数学证明的简单树形 DP
P4395 [BOI2003] Gem 气垫车
给你一个树，对每个点赋权，保证相邻节点权值不相等，求权值和最小值。
一开始想填 1, 2 就行，但是瞄了一眼讨论发现是假的。
老实 DP，还是比较简单的，设 \(f_{u,k}\) 表示 \(c_u=k\) 时，子树内的权值和的最小值。则
时间复杂度是 \(O(nk^2)\) 不可接受，但是可以证明 \(k\) 是 \(\log n\) 级别的，时间复杂度 \(O(n\log^2 n)\)
证明：见 CNCAGN 博客
点击查看代码
#include<bits/stdc++.h>
#define int long long
const int maxn=1e4+3;
const int logn=20;
using namespace std;
int n,f[maxn][logn+3];
vector<int>e[maxn];
void dfs(int u,int fa){
for(int i=1;i<=logn;i++){
f[u][i]=i;
}
for(int v:e[u]){
if(v!=fa){
dfs(v,u);
for(int i=1;i<=logn;i++){
int mi=maxn*(logn+3);
for(int j=1;j<=logn;j++){
if(i==j) continue;
mi=min(mi,f[v][j]);
}
f[u][i]+=mi;
}
}
}
}
signed main(){
cin>>n;
for(int i=1,u,v;i<n;i++){
cin>>u>>v;
e[u].emplace_back(v);
e[v].emplace_back(u);
}
dfs(1,0);
int ans=maxn*(logn+3);
for(int i=1;i<=logn;i++) ans=min(ans,f[1][i]);
cout<<ans;
return 0;
}
刷表法 DP
应该是最经典的 DP 之一。
P3558 [POI2013] BAJ-Bytecomputer
给定一个长度为 \(n\) 的只包含 \(-1,0,1\) 的数列 \(a\)，每次操作可以使 \(a_i\gets a_i+a_{i-1}\)，求最少操作次数使得序列单调不降。如果不可能通过该操作使得序列单调不降，请输出 BRAK。
数据范围：\(1\le n\le 10^6\)。
设 \(f_{i,-1/0/1}\) 表示 \(i\) 位为 \(-1/0/1\) 时的最小操作次数，\(i=1\) 时。接下来分类讨论：
- 当 \(a_i=-1\)
\(f_{i,-1}=f_{i-1,-1}\)，当前位为 \(-1\) 时，只能从 \(-1\) 转移，且不需要任何操作；
当前一位为 \(1\) 时，才能将当前位的值提高，所以要把当前位的 \(-1\) 变成 \(0/1\) 都需要消耗操作次数，则有转移：\(f_{i,0}=\begin{cases}\min(f_{i-1,-1},f_{i-1,0})+1&a_{i-1}=1\\ +\infty&\text{otherwise}\end{cases}\)；
其他情况差不多，就看代码罢。
点击查看代码
#include<bits/stdc++.h>
#define int long long
using
namespace
std;
const int maxn=1e6+3;
const int inf=0x3f3f3f3f;
int f[maxn][3],n;
int a[maxn];
signed main(){
cin>>n;
for(int i=1;i<=n;i++) cin>>a[i];
f[1][0]=f[1][1]=f[1][2]=inf;
f[1][a[1]+1]=0;
for(int i=2;i<=n;i++){
if(a[i]==-1){
f[i][0]=f[i-1][0];
if(a[i-1]==1) f[i][1]=min(f[i-1][1],f[i-1][0])+1;
else f[i][1]=inf;
if(a[i-1]==1) f[i][2]=min(min(f[i-1][2],f[i-1][1]),f[i-1][0])+2;
else f[i][2]=f[i-1][2]+2;
}else if(a[i]==0){
f[i][0]=f[i-1][0]+1;
f[i][1]=min(f[i-1][1],f[i-1][0]);
if(a[i-1]==1) f[i][2]=min(min(f[i-1][2],f[i-1][1]),f[i-1][0])+1;
else f[i][2]=f[i-1][2]+1;
}else{
f[i][0]=f[i-1][0]+2;
if(a[i-1]==-1) f[i][1]=min(f[i-1][1],f[i-1][0])+1;
else f[i][1]=f[i][0]+1;
f[i][2]=min(min(f[i-1][2],f[i-1][1]),f[i-1][0]);
}
}
int t=min(f[n][0],min(f[n][1],f[n][2]));
if(t==inf) cout<<"BRAK";
else cout<<t;
return 0;
}
