Codeforces Round 943 (Div. 3)
A. Maximize?
给你一个整数 \(x\) 。您的任务是找出任意一个整数 \(y\) ,使得 \(\gcd(x,y)+y\) 最大。 \((1\le y<x)\) 使得 \(\gcd(x,y)+y\) 最大。
注意,如果有不止一个 \(y\) 满足该语句的要求,则允许你找出任何一个。
\(\gcd(a,b)\) 是 \(a\) 和 \(b\) 的最大公约数。例如, \(\gcd(6,4)=2\) 。
输入
第一行包含一个整数 \(t\) ( \(1 \le t \le 1000\) ) - 测试用例数。
下面每行 \(t\) 都包含一个整数 \(x\) ( \(2 \le x \le 1000\) )。
暴力模拟发现当 \(y=x-1\) 时总是有原式最大,输出 \(x-1\) 即可。
点击查看代码
#include<bits/stdc++.h>
#define int long long
using namespace std;
int t,n;
signed main(){
cin>>t;
while(t--){
cin>>n;
cout<<n-1<<'\n';
}
return 0;
}
B. Prefiquence
给你两个二进制字符串 \(a\) 和 \(b\) 。二进制字符串是由字符 "0 "和 "1 "组成的字符串。
您的任务是确定最大可能的数字 \(k\) ,使得长度为 \(k\) 的字符串 \(a\) 的前缀是字符串 \(b\) 的子序列。
如果 \(a\) 可以通过删除几个(可能是零个或全部)元素从 \(b\) 得到,则序列 \(a\) 是序列 \(b\) 的子序列。
输入
第一行包含一个整数 \(t\) ( \(1 \le t \le 10^4\) ) - 测试用例数。
每个测试用例的第一行包含两个整数 \(n\) 和 \(m\) ( \(1\le n,m \le 2 \cdot 10^5\) ) - 分别是字符串 \(a\) 的长度和字符串 \(b\) 的长度。
每个测试用例的第二行包含长度为 \(n\) 的二进制字符串 \(a\) 。
每个测试用例的第三行包含长度为 \(m\) 的二进制字符串 \(b\) 。
保证所有测试用例的值 \(n\) 之和不超过 \(2 \cdot 10^5\) 。同样,所有测试用例中 \(m\) 的值之和不超过 \(2 \cdot 10^5\) 。
贪心求最大答案。
点击查看代码
#include<bits/stdc++.h>
#define int long long
using namespace std;
int T,n,m,cnt;
char s[200003],t[200003];
signed main(){
cin>>T;
while(T--){
cin>>n>>m;
cin>>s>>t;
int pos=0;
for(int i=0;s[i];i++){
for(;t[pos];pos++){
if(t[pos]==s[i]){cnt++;pos++;break;}
}
if(!t[pos])break;
}
cout<<cnt<<'\n';cnt=0;
}
return 0;
}
C. Assembly via Remainders
给你一个数组 \(x_2,x_3,\dots,x_n\) 。你的任务是找出任意一个数组 \(a_1,\dots,a_n\) ,其中:
- \(1\le i\le n\) 中的 \(1\le a_i\le 10^9\) 。
- \(x_i=a_i \bmod a_{i-1}\) 代表所有 \(2\le i\le n\) 。
这里的 \(c\bmod d\) 表示整数 \(c\) 除以整数 \(d\) 的余数。例如 \(5 \bmod 2 = 1\) , \(72 \bmod 3 = 0\) , \(143 \bmod 14 = 3\) .
**注意,如果有一个以上的 \(a\) 满足该语句的要求,你可以找到任何一个。
看代码,用模运算展开式(\(x=a\bmod a'\to a=qa'+x\))即可。
点击查看代码
#include<bits/stdc++.h>
#define int long long
using namespace std;
int T,n,x[503],a[503];
signed main(){
cin>>T;
while(T--){
cin>>n;
for(int i=2;i<=n;i++) cin>>x[i];
a[1]=x[2]+1;
for(int i=2;i<=n;i++){
a[i]=(max(x[i+1]-x[i],0ll)/a[i-1]+1)*a[i-1]+x[i];
}
for(int i=1;i<=n;i++) cout<<a[i]<<" \n"[i==n];
}
return 0;
}
/*
xi=ai mod ai-1
ai=pi*ai-1+xi
ai-1=pi-1*ai-2+xi-1
a2=p2*a1+x2
a3=p3*a2+x3
*/
D. Permutation Game
Bodya 和 Sasha 发现了一个排列 \(p_1,\dots,p_n\) 和一个数组 \(a_1,\dots,a_n\) 。他们决定玩一个著名的 "排列游戏"。
长度为 \(n\) 的排列是由 \(n\) 个不同的整数组成的数组,这些整数从 \(1\) 到 \(n\) 按任意顺序排列。例如, \([2,3,1,5,4]\) 是一个排列,但 \([1,2,2]\) 不是一个排列( \(2\) 在数组中出现了两次), \([1,3,4]\) 也不是一个排列( \(n=3\) ,但数组中有 \(4\) )。
它们都在排列中选择了一个起始位置。
对局持续了 \(k\) 个回合。棋手同时下棋。在每个回合中,每个棋手都会发生两件事:
- 如果棋手当前的位置是 \(x\) ,那么他的得分就会增加 \(a_x\) 。
- 然后棋手要么停留在当前位置 \(x\) ,要么从 \(x\) 移动到 \(p_x\) 。
在整整 \(k\) 个回合后,得分较高的一方即为获胜者。
知道了博迪娅的起始位置 \(P_B\) 和萨沙的起始位置 \(P_S\) 后,如果双方都想获胜,那么谁会赢得这盘棋呢?
一眼题。显然 S,B 走的路径是一条链然后到某个点停下,暴力更新贡献即可。
点击查看代码
#include<bits/stdc++.h>
#define int long long
using namespace std;
int T,n,a[200003],p[200003],k,pb,ps,anb,ans;
signed main(){
cin>>T;
while(T--){
cin>>n>>k>>pb>>ps;
for(int i=1;i<=n;i++) cin>>p[i];
for(int i=1;i<=n;i++) cin>>a[i];
int eb=pb,es=ps,totb=0,tots=0,lenb=0,lens=0;
do{
totb+=a[eb];lenb++;
anb=max(anb,totb+(k-lenb)*a[eb]);
eb=p[eb];
}while(eb!=pb&&lenb<=k);
do{
tots+=a[es];lens++;
ans=max(ans,tots+(k-lens)*a[es]);
es=p[es];
}while(es!=ps&&lens<=k);
if(anb>ans) cout<<"Bodya\n";
else if(anb<ans) cout<<"Sasha\n";
else cout<<"Draw\n";
anb=ans=0;
}
return 0;
}
E. Cells Arrangement
给你一个整数 \(n\) 。您在网格 \(n\times n\) 中选择 \(n\) 单元格 \((x_1,y_1), (x_2,y_2),\dots,(x_n,y_n)\) ,其中 \(1\le x_i\le n\) 和 \(1\le y_i\le n\) .
假设 \(\mathcal{H}\) 是任意一对单元格之间不同的曼哈顿距离集合。你的任务是最大化 \(\mathcal{H}\) 的大小。注释中给出了集合及其构造的例子。
**如果存在多个解,你可以输出任意一个。
单元格 \((x_1,y_1)\) 和 \((x_2,y_2)\) 之间的曼哈顿距离等于 \(|x_1-x_2|+|y_1-y_2|\) 。
申金找规律题。
这是题解的规律。
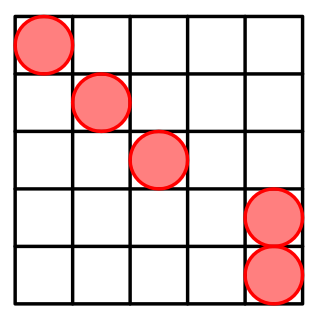
然而我认为不是最优。
我的考场解法:以 \(n=9\) 为例

- 显然左上右下肯定要放。
16 - 在第一列从第二个开始隔一个放一个,这样有一个好处,这样构造可以保证 \(dis<\frac n2\) 的被构造,所以这里
0 1 2 3 4 5 6 7。再考虑到右下角的贡献,即9 11 13 15,剩下的距离就用与右下角距离为 1 的点就行了,即8 10 12 14。 - 你惊奇地发现这样构造只要 7 个点就够了,这是我两次 WA 的原因(少输出点)
- 你惊奇地发现 \(n\le 4\) 会出问题,没关系,判掉即可。
是不是爆标了
点击查看代码
#include<bits/stdc++.h>
#define int long long
using namespace std;
int T,n;
signed main(){
cin>>T;
while(T--){
cin>>n;
cout<<"1 1\n";
if(n==4){
cout<<n<<' '<<n<<'\n';
cout<<"1 2\n";
cout<<n<<' '<<n-2<<'\n';
continue;
}
for(int i=2;i<=n;i+=2){
cout<<"1 "<<i<<'\n';
}
if(n>2) cout<<n<<' '<<n<<'\n';
if(n>3) cout<<n<<' '<<n-1<<'\n';
if(n>6) cout<<(n+1)/2<<' '<<(n+1)/2<<'\n';
}
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号