补题 DAY3,4

P2474 [SCOI2008] 天平

你有 $n$ 个砝码，均为 $1$ 克， $2$ 克或者 $3$ 克。你并不清楚每个砝码的重量，但你知道其中一些砝码重量的大小关系。你把其中两个砝码 A 和 B 放在天平的左边，需要另外选出两个砝码放在天平的右边。问：有多少种选法使得天平的左边重( $c_{1}$ )、一样重( $c_{2}$ )、右边重( $c_{3}$ )？（只有结果保证唯一确定的选法才统计在内）， $4 \leq n \leq 50$ 。

转化题意：

- $\to - 2 \leq i - j \leq - 1$
+ $\to 1 \leq i - j \leq 2$
= $\to 0 \leq i - j \leq 0$
? $\to - 2 \leq i - j \leq 2$

即可差分约束，记 $m i [i] [j]$ 为 $i, j$ 的左半边限制， $m x [i] [j]$ 为 $i, j$ 的右半边限制，然后分别对 $m i, m x$ 跑最长、最短路 (Floyd) 求出每对硬币重量差的范围为 $[m i [i] [j], m x [i] [j]]$ 。

然后统计答案，枚举 $i, j$ ：

$A + B > i + j \to A - i > j - B / B - i > j - A$ ，即当 $m i [A] [i] > m x [j] [B]$ 或 $m i [B] [i] > m x [j] [A]$ 时， $c_{1}$ 加 $1$ 。
$A + B < i + j \to j - B > A - i / j - A > B - i$ ，即当 $m i [j] [B] > m x [A] [i]$ 或 $m i [j] [A] > m x [B] [i]$ 时， $c_{3}$ 加 $1$ 。
$A + B = i + j \to A - i = j - B, B - i = j - A / B - i = j - A, A - i = j - B$ ，为保证结果唯一，需要两边区间最大等于最小，最小等于最大时， $c_{2}$ 加 $1$ 。

时间复杂度 $O (n^{3})$ 。

点击查看代码

#include<bits/stdc++.h>
using namespace std;
int n,a,b,cnt1,cnt2,cnt3;
int mi[53][53],mx[53][53];
signed main(){
	cin>>n>>a>>b;
	for(int i=1;i<=n;i++){
		for(int j=1;j<=n;j++){
			char ch;
			cin>>ch;
			if(ch=='+'){
				mi[i][j]=1;
				mx[i][j]=2;
			}else if(ch=='-'){
				mi[i][j]=-2;
				mx[i][j]=-1;	
			}else if(ch=='='){
				mi[i][j]=0;
				mx[i][j]=0;
			}else{
				mi[i][j]=-2;
				mx[i][j]=2;
			}
		}
	}
	for(int k=1;k<=n;k++)
		for(int i=1;i<=n;i++)
			for(int j=1;j<=n;j++)
				mx[i][j]=min(mx[i][j],mx[i][k]+mx[k][j]),
				mi[i][j]=max(mi[i][j],mi[i][k]+mi[k][j]);
	for(int i=1;i<=n;i++){
		for(int j=1;j<i;j++){
			if(i==a||i==b||j==a||j==b) continue;
			if(mi[i][a]>mx[b][j]||mi[i][b]>mx[a][j]) cnt3++;
			if((mx[i][a]==mi[b][j]&&mi[i][a]==mx[b][j])
			 ||(mx[i][b]==mi[a][j]&&mi[i][b]==mx[a][j])) cnt2++;
			if(mi[a][i]>mx[j][b]||mi[b][i]>mx[j][a]) cnt1++;
		}
	}
	cout<<cnt1<<' '<<cnt2<<' '<<cnt3;
	return 0;
}

P2371 [国家集训队] 墨墨的等式

墨墨突然对等式很感兴趣，他正在研究 $\sum_{i = 1}^{n} a_{i} x_{i} = b$ 存在非负整数解的条件，他要求你编写一个程序，给定 $n, a_{1 \dots n}, l, r$ ，求出有多少 $b \in [l, r]$ 可以使等式存在非负整数解。

对于 $100 %$ 的数据， $n \leq 12$ ， $0 \leq a_{i} \leq 5 \times 10^{5}$ ， $1 \leq l \leq r \leq 10^{12}$ 。

点击查看代码

#include<bits/stdc++.h>
#define int long long
using namespace std;
const int maxn=5e5+3;
int l,r,a[30],n,flag;
struct di{
	int dis,id;
	bool operator<(const di o)const{return dis>o.dis;}
};
priority_queue<di>q;
struct edge{
	int v,w;
	edge(int v=0,int w=0): v(v),w(w){}
};
vector<edge>e[maxn];
int dis[maxn];
void dijkstra(){
	for(int i=0;i<=5e5;i++) dis[i]=0x3f3f3f3f3f3f3f3f;
	q.push({dis[1]=0,1});
	while(!q.empty()){
		di u=q.top(); q.pop();
		if(dis[u.id]==u.dis){
			for(edge v:e[u.id]){
				if(dis[v.v]>dis[u.id]+v.w)
					q.push({dis[v.v]=dis[u.id]+v.w,v.v});
			}
		}
	}
}
signed main(){
	cin>>n>>l>>r;
	for(int i=1;i<=n;i++) cin>>a[i],flag|=a[i]==1;
	sort(a+1,a+n+1);
	if(flag){ cout<<r-l+1; return 0; }
	for(int i=0;i<a[1];i++)
		for(int j=2;j<=n;j++)
			e[i].emplace_back(edge((i+a[j])%a[1],a[j]));
	dijkstra();
	int ansl=0,ansr=0;
	for(int i=0;i<a[1];i++){
		if(l-1>=dis[i]) ansl+=(l-1-dis[i])/a[1]+1;
		if(r>=dis[i]) ansr+=(r-dis[i])/a[1]+1;
	}
	cout<<ansr-ansl;
	return 0;
}

AGC013D Piling Up

不已知初始情况。但是考虑操作的变化量，横轴为操作次数，纵轴为白球个数。可以发现在图像上可以表示为 V(0), V\(-1), /(+1) 等形状，统计形状数。

但是直接统计会重。

有一个技巧：只统计可以使 $y = 0$ 的操作序列。

为什么这样子可以？

首先，从同一个点出发的路径是不存在重复的。

那么重复一定存在于从不同点出发的路径中，并且一定可以由一条路径上下平移得到另一条路径。

我们可以用反证法，假设在只统计有 $y = 0$ 的情况时，统计仍然有重复，设重复统计的这两条路径记为 $f (x), g (x)$ 。

因为两者可以上下平移得到，所以 $f (x) = g (x) + k$ 。

当 $f (x) = 0$ 时， $g (x) = - k$ ，因为 $g (x)$ 有意义，所以 $g (x) = - k \leq 0$ （球的数目不会是负数）。

当 $g (x) = 0$ 时，同理有 $k \geq 0$ 。因此 $k = 0$ ， $f (x) = g (x)$ ， $f (x), g (x)$ 是同一条路径。

故此时不存在重复。

综上，设 $f [i] [j] [0 / 1]$ 为第 $i$ 步操作，白球有 $j$ 个，否/是存在一次操作使得 $j = 0$ 。

有转移：

$j \geq 1 :$
- $j = 1 :$
  $f [i + 1] [j - 1] [1] + = f [i] [j] [0]$
- else:
  $f [i + 1] [j - 1] [0] + = f [i] [j] [0]$
  $f [i + 1] [j - 1] [1] + = f [i] [j] [1]$

其余同理，见代码：

点击查看代码

#include<bits/stdc++.h>
#define int long long
const int mod=1e9+7;
const int maxn=3003;
using namespace std;
int f[maxn][maxn][2];
// 操作 i 次，有 j 个白，是否经历过 j=0 
int n,m,ans;
signed main(){
	cin>>n>>m;
	for(int j=1;j<=n;j++) f[0][j][0]=1;
	f[0][0][1]=1;
	for(int i=0;i<m;i++){
		for(int j=0;j<=m;j++){
			int &no=f[i][j][0],&ye=f[i][j][1];
			no%=mod,ye%=mod;
			if(j>=1){
				if(j==1) f[i+1][j-1][1]+=no;
				else f[i+1][j-1][0]+=no;
				f[i+1][j-1][1]+=ye;
				if(j==1) f[i+1][j][1]+=no;
				else f[i+1][j][0]+=no;
				f[i+1][j][1]+=ye;
			}
			if(j<n){
				f[i+1][j+1][0]+=no;
				f[i+1][j+1][1]+=ye;
				f[i+1][j][0]+=no;
				f[i+1][j][1]+=ye;
			}
		}
	}
	for(int i=0;i<=n;i++) ans=(ans+f[m][i][1])%mod;
	cout<<ans;
	return 0;
}

CF1895F Fancy Arrays

矩阵乘法+计数

点击查看代码

#include<bits/stdc++.h>
using namespace std;
#define int long long
const int mod=1e9+7;
int n,x,K,t;
struct matrix{
	int a[103][103];
	matrix(){}
	matrix friend operator*(matrix a,matrix b){
		matrix g;
		for(int i=1;i<=x;i++)
			for(int k=1;k<=x;k++)
				for(int j=1;j<=x;j++)
					g.a[i][j]=(g.a[i][j]+a.a[i][k]*b.a[k][j]%mod)%mod;
		return g;
	}
}base;
int qpow(int a,int b){
	int ans=1;
	for(;b;b>>=1,a=a*a%mod) 
		if(b&1) ans=ans*a%mod;
	return ans;
}
matrix qpow(matrix a,int b){
	for(;b;b>>=1,a=a*a) 
		if(b&1) base=base*a; 
	return base;
}
signed main(){
	cin>>t;
	while(t--){
		cin>>n>>x>>K;
		matrix f;
		for(int i=1;i<=x;i++)
			for(int j=1;j<=x;j++)
				f.a[i][j]=abs(i-j)<=K;
		for(int i=1;i<=x;i++) base.a[1][i]=1;
		matrix g=qpow(f,n-1);
		int sum=0;
		for(int i=1;i<=x;i++){
			sum=(sum+g.a[1][i])%mod;
		}
		cout<<(qpow(K<<1ll|1ll,n-1)*(x+K)%mod-sum+mod)%mod<<'\n';
	}
	return 0;
}

AGC013E Placing Squares

给定一个长度为 $n$ 的木板，木板上有 $m$ 个标记点，距离木板左端点的距离分别为 $X_{i}$ ，现在你需要在木板上放置一些不相交正方形，正方形需要满足

正方形的边长为整数
正方形底面需要紧贴木板
正方形不能超出木板，正方形要将所有的木板覆盖
标记点的位置不能是两个正方形的交界处

下面是一些满足条件与不满足条件的例子

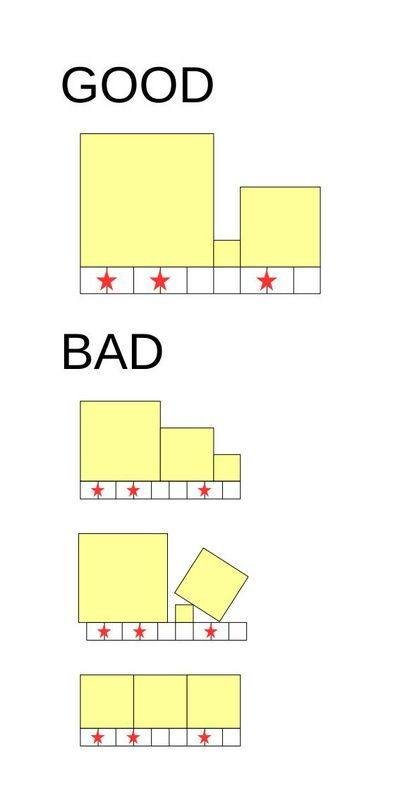
一种合法的正方形放置方案的贡献为所有正方形面积的乘积，也就是为 $\prod_{i = 1}^{k} a_{i}^{2}$ ， $a_{i}$ 为正方形的边长。

请你求出所有合法方案的贡献之和，答案对 $10^{9} + 7$ 取模。

$n \leq 10^{9}$ ， $m \leq 10^{5}$ 。

转化题意，即求

在 $n$ 个格子之间放若干隔板
不能在标记格子集合与其下一个格子之间放隔板
在相邻隔板之间的恰好放 2 个不同颜色的球
的方案数。

其中最后一个要求维护了 $a^{2}$ ，非常巧妙。

设 $f_{i, j}$ 表示考虑到下标 $i$ ，当前到上一个隔板中放了 $j (j \in [0, 2])$ 个球的方案数。

注意到一旦放隔板，就只能从 $f_{i, 2}$ 转移。

对于非标记格子（ $A$ ）：

$f_{i + 1, 0} = f_{i, 0} + f_{i, 2}$
$f_{i + 1, 1} = (2 f_{i, 0} + f_{i, 1}) + 2 f_{i, 2}$ （两倍是因为有两种不同颜色）
$f_{i + 1, 2} = (f_{i, 0} + f_{i, 1} + f_{i, 2}) + f_{i, 2} = f_{i, 0} + f_{i, 1} + 2 f_{i, 2}$ （前半部分为不放隔板的情况，上面的同理）

对于标记格子（ $B$ ），不能放隔板，因此球多的只能从球少的转移过来：

$f_{i + 1, 0} = f_{i, 0}$
$f_{i + 1, 1} = 2 f_{i, 0} + f_{i, 1}$
$f_{i + 1, 2} = f_{i, 0} + f_{i, 1} + f_{i, 2}$

然后扔到矩阵上面：

A = [\begin{matrix} 1 & 0 & 1 \\ 2 & 1 & 2 \\ 1 & 1 & 2 \end{matrix}], B = [\begin{matrix} 1 & 0 & 0 \\ 2 & 1 & 0 \\ 1 & 1 & 1 \end{matrix}]

答案就为（记 $Δ X$ 为 $X$ 的差分数组）：

A^{n - X_{m} - 1} \prod_{i = 1}^{m} A^{Δ X_{i} - 1} B

矩阵快速幂，时间复杂度 $O (\log n + m)$ 。

点击查看代码

#include<bits/stdc++.h>
#define int long long
using namespace std;
const int mod=1e9+7;
struct mat{
	int a[3][3];
	mat(){memset(a,0,sizeof(a));}
	mat operator *(const mat &rhs){
		mat res;
		for(int i=0;i<3;i++) for(int j=0;j<3;j++) for(int k=0;k<3;k++)
			res.a[i][j]+=a[i][k]*rhs.a[k][j];
		for(int i=0;i<3;i++) for(int j=0;j<3;j++) res.a[i][j]%=mod;
		return res;
	}
}u,v,ans;
int n,m,lp=-1;
void qpow(mat a,int b,mat &c){for(;b;b>>=1,a=a*a) if(b&1) c=a*c;}
signed main(){
	cin>>n>>m; ans.a[0][0]=1;
	u.a[0][0]=1, u.a[0][1]=0, u.a[0][2]=1,
	u.a[1][0]=2, u.a[1][1]=1, u.a[1][2]=2,
	u.a[2][0]=1, u.a[2][1]=1, u.a[2][2]=2,
	v.a[0][0]=1, v.a[0][1]=0, v.a[0][2]=0,
	v.a[1][0]=2, v.a[1][1]=1, v.a[1][2]=0,
	v.a[2][0]=1, v.a[2][1]=1, v.a[2][2]=1;
	for(int i=1,p;i<=m;i++){
		cin>>p;
		qpow(u,p-lp-1,ans);
		ans=v*ans; lp=p;
	}
	qpow(u,n-lp-1,ans);
	cout<<ans.a[2][0];
	return 0;
}

CF622F The Sum of the k-th Powers

首先可以暴力求出 $n = 1 \sim k + 2$ 的答案，记录在 $s$ 中。

然后我们需要证明 $s_{n}$ 是关于 $n$ 的 $k + 1$ 次多项式。

先证明一个引理，对于一个任意阶的等差数列 $a$ ，存在一个 $x$ 的 $k$ 次多项式 $f (x) = \sum_{i = 0}^{k} u_{i} x^{i}$ 为 $a$ 的通项公式，记 $b$ 为 $a$ 的差分数列，则 $b$ 的通项为 $k - 1$ 次多项式。

根据定义， $b$ 的通项为 $Δ f (x) = f (x) - f (x - 1)$ （有些微积分的感觉？），略去其他 $\leq k$ 次的项，则 $Δ f (x) \sim u_{k} x^{k} - u_{k} (x - 1)^{k}$ 。

利用二项式定理展开，再略去 $\leq k$ 的项，则 $Δ f (x) \sim u_{k} x^{k} - u_{k} x^{k} = 0$ ，于是便不存在了 $k$ 次项，即 $b$ 的通项为 $k - 1$ 次多项式，证毕。

设 $t_{i} = s_{i} - s_{i - 1}$ ，则 $t_{i} = \sum_{j = 1}^{i} j^{k} - \sum_{j = 1}^{i - 1} j^{k} = i^{k}$ ，是一个关于 $i$ 的 $k$ 次多项式，所以 $s_{i}$ 是关于 $i$ 的 $k + 1$ 次多项式， $s_{n}$ 是关于 $n$ 的 $k + 1$ 次多项式。

至此， $s_{n}$ 次数就确定了，但是系数不确定，所以就可以通过拉格朗日插值确定这个多项式。

由拉差得

s_{n} = \sum_{i = 1}^{k + 2} s_{i} \prod_{j \neq i} \frac{n - j}{i - j}

点击查看代码

#include<bits/stdc++.h>
#define int long long
const int maxk=1e6+3;
const int mod=1e9+7;
using namespace std;
int n,k;
int s[maxk],pre[maxk],suf[maxk],ifac[maxk];
int qpow(int a,int b){
	int ans=1;
	for(;b;b>>=1,a=a*a%mod) if(b&1) ans=ans*a%mod;
	return ans;
}
signed main(){ 
	cin>>n>>k;
	pre[0]=ifac[0]=suf[k+3]=ifac[k+3]=1;
	for(int i=1;i<=k+2;i++){
		s[i]=(s[i-1]+qpow(i,k))%mod;
		pre[i]=pre[i-1]*(n-i)%mod;
		ifac[k+3]=ifac[k+3]*i%mod;
	}
	ifac[k+3]=ifac[k+3]*(k+3)%mod;
	ifac[k+3]=qpow(ifac[k+3],mod-2);
	if(n<=k+2){
		cout<<s[n];
		return 0;
	}
	for(int i=k+2;i;i--){
		suf[i]=suf[i+1]*(n-i)%mod;
		ifac[i]=ifac[i+1]*(i+1)%mod;
	}
	int sn=0;
	for(int i=1,op=((k-i+2)&1?-1:1);i<=k+2;i++,op=((k-i+2)&1?-1:1)){
		s[i]=s[i]*pre[i-1]%mod*suf[i+1]%mod*ifac[i-1]%mod*ifac[k-i+2]%mod;
		if((k-i+2)&1) sn=(sn-s[i]+mod)%mod;
		else sn=(sn+s[i])%mod;
	}
	cout<<sn;
	return 0;
}