八大基本排序
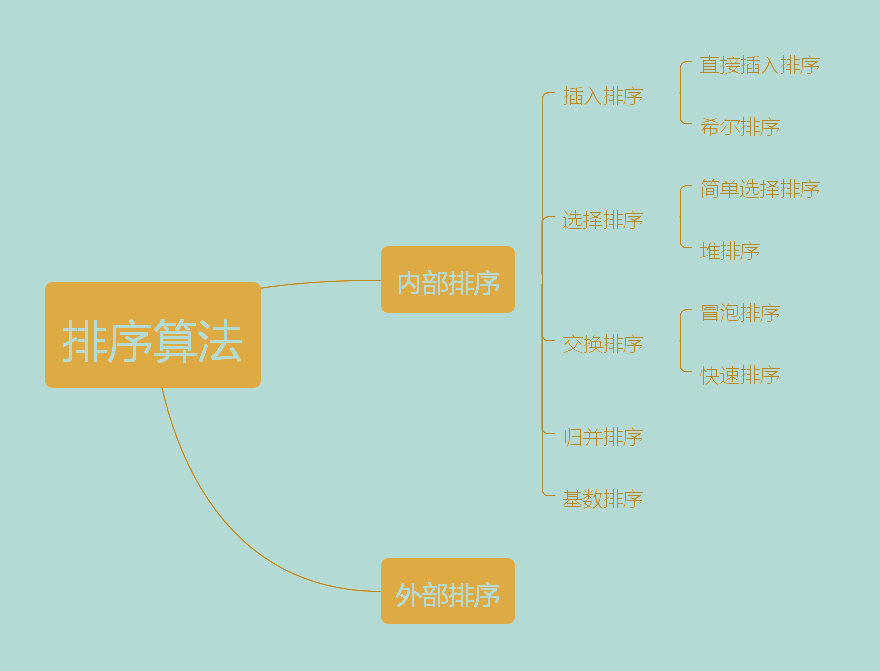
内部排序:在排序期间数据对象全部存放在内存的排序
外部排序:指在排序期间对象太多,不能同时存放在内存中,必须根据排序过程的要求,不断在内、外存间移动。
效率的衡量:
内部排序:比较的次数(即时间复杂度)
外部排序:IO次数
性能比较:

稳定:待排序序列中相同数字的顺序 在 排好序后,顺序不发生改变。

直接插入排序:
/** * 直接插入排序 * 思想: 将待排元素 与 已经排好序的元素进行比较 * 升序:(逆序比较)若待排元素 小于 已排元素,则交换位置; 若待排元素 大于 已排元素,则不交换,停止比较。 */ public class InsertSort { public static void main(String[] args){ int[] arr = new int[]{12, 3, 9, 24, 45, 17}; for(int i = 1; i < arr.length; i++){ //待比较元素的小标 从第二个元素开始 // 如果j是 从0~(i-1) 那么比较会涉及到元素后移,增加时间复杂度 for(int j = i-1; j >= 0; j--){ if(arr[i] < arr[j]){ // 直接插入排序稳定 如果是arr[i] <= arr[j] 则不稳定 int temp = arr[i]; arr[i] = arr[j]; arr[j] = temp; } } } for(int x : arr){ System.out.print(x + " "); } } }
最好的情况:待排数组已经排好序, 待排元素只需跟已排元素比较一次 O(n)
最坏情况: 待排数组与预期顺序全部逆序,每个待排元素需要与全部的已排元素比较一次 O(
)
使用场景:规模较小或者基本有序
希尔排序:是插入排序的改进版
public class SheelSort { public static void main(String[] args){ int[] arr = new int[]{12, 3, 9, 24, 45, 17, 33, 7, 11, 15}; for(int gap = arr.length/2; gap >= 1; gap /= 2){ // 将arr[i]插入到每组 对应的位置 for(int i = gap; i < arr.length; i++){ // i 是每组元素的第二个元素 int d = arr[i]; int j; // 待排元素是: arr[i], 已排元素是: i-gap, i-2gap.... 逆着比较 for(j = i-gap; j >= 0 && d < arr[j]; j -= gap){ arr[j+gap] = arr[j]; // 若已排元素大于待排元素temp 则往后移动 } arr[j+gap] = d; } } for(int x : arr){ System.out.print(x + " "); } } }

在进行排序的过程中,并不是对某组排完序后再对另一组排序,而是各组轮流排序。(可以设个断点看看变化)
直接选择排序:
/** * 算法思想:进行n-1次循环,在第i(从0开始)次循环中,在待排序列中找到最小(大)值的下标,看是否与i相等, * 如果不相等,则两个位置上的元素进行交换 */ public class SelectSort { public static void main(String[] args){ int[] arr = new int[]{12, 3, 9, 24, 45, 17}; for(int i = 0; i < arr.length-1; i++){ // 循环次数 int min = i; for(int j = i+1; j < arr.length; j++){ //在待排序列中 找到最小元素的小标 if(arr[j] < arr[min]){ min = j; } } if(min != i){ // 如果最小元素不是 arr[i] 则arr[i]与最小元素进行交换 int temp = arr[i]; arr[i] = arr[min]; arr[min] = temp; } } for(int x : arr){ System.out.print(x + " "); } } }
堆排序:
https://www.jianshu.com/p/0d383d294a80

public class HeahSort { public static void swap(int[] arr, int i, int j){ int temp = arr[i]; arr[i] = arr[j]; arr[j] = temp; } public static void adjust(int[] arr, int pos, int n){ int j = 2 * pos; //左孩子下标 while(j <= n){ // 先取 左右孩子中较大的值 if ((j + 1 <= n) && arr[j+1] > arr[j]){ j++; } // 比较孩子节点与父节点 if (arr[pos] >= arr[j]){ break; //不需要交换 } swap(arr, pos, j); // 还要继续比较 与 父节点交换后的这个节点 其孩子节点是否小于这个节点 pos = j; j = 2 * pos; } } public static void buildHeap(int[] arr, int n){ // 根据完全二叉树结点的特点 父节点n 左孩子2n+1, 右孩子:2n+2 (下标从0开始) // 先调整:从最后一个父节点开始调整 建大根堆 父节点大于孩子节点 for(int i = n/2; i > 0; i--){ adjust(arr, i, n); } } public static void heapSort(int[] arr, int n){ // 每次都是 “最后一个元素” 与 第一个元素进行交换 然后调整 for(int i = n; i > 1; i--){ swap(arr, i, 1); buildHeap(arr, i-1); // 重建堆 } } public static void main(String[] args){ // 数据从下标 1 开始,方便计算最后一个父节点 int[] arr = new int[]{0, 12, 3, 9, 24, 45, 17}; buildHeap(arr, arr.length-1); // 数组 和 最后一个元素的下标 heapSort(arr, arr.length-1); for(int i = 1; i < arr.length; i++){ System.out.print(arr[i] + " "); } } }
冒泡排序:
/** * 冒泡排序 * 算法思想:比较交换 */ public class BubbleSort { public static void main(String[] args){ int[] arr = new int[]{12, 3, 9, 24, 45, 17}; for(int i = 0; i < arr.length-1; i++){ boolean flag = false; // 看序列是否已经有序 没有交换就表示序列已经有序 for(int j = 0; j < arr.length-i-1; j++){ //从下标0开始,只需要比较到待排序列的倒数第二个元素即可 if(arr[j] > arr[j+1]){ flag = true; int temp = arr[j]; arr[j] = arr[j+1]; arr[j+1] = temp; } } if(flag == false) { break; } } for(int x : arr){ System.out.print(x + " "); } } }
最好情况: 待排序列已经有序,就只需要一个循环的比较即可 O(n)
最坏情况: 待排序列与想象中的序列完全逆序 O(
)
快速排序:
/** * 算法思想:找一个基准数,把比基准数小的数往左移, 比基准数大的往右移,每一次的排序都会把基准数放在正确位置 */ public class QuickSort { public static void quickSort(int[] arr, int start, int end){ if(start >= end) return ; int point = arr[start]; int low = start, high = end; while(low < high){ while(low < high && arr[high] >= point){ high--; } // 循环结束时, arr[high] < point if(low < high){ arr[low] = arr[high]; low++; } while(low < high && arr[low] <= point){ low++; } // 循环结束时,arr[low] > point if(low < high){ arr[high] = arr[low]; high--; } } arr[high] = point; //把point放在正确的位置上 point左边就是比point小的数 右边就是比point大的数 quickSort(arr, start, high-1); quickSort(arr, high+1, end); } public static void main(String[] args){ int[] arr = new int[]{12, 3, 9, 24, 45, 17}; quickSort(arr, 0, arr.length-1); for(int x : arr){ System.out.print(x + " "); } } }
归并排序:
/** * 归并排序: * 算法思想: 分治+合并 先拆分然后组内排序,把两组有序的合并成一组 */ public class MergeSort { /** * 合并 */ public static void merge(int[] arr, int start, int mid, int end){ int lenL = mid - start + 1; // 元素个数 int lenR = end - mid; int[] arrL; int[] arrR; arrL = Arrays.copyOfRange(arr, start, mid+1); // [左闭 右开) arrR = Arrays.copyOfRange(arr, mid+1, end+1); int i = 0, j = 0, n = start; int len = Math.min(lenL, lenR); while(i < lenL && j < lenR){ if(arrL[i] <= arrR[j]){ arr[n++] = arrL[i++]; } else{ arr[n++] = arrR[j++]; } } while(i < lenL){ arr[n++] = arrL[i++]; } while(j < lenR){ arr[n++] = arrR[j++]; } } public static void mergeSort(int[] arr, int start, int end){ if(start == end) return ; // 元素个数为1 就不用分组啦 int mid = (start + end) / 2; // 向下取整 // 先分成左右两组 直至组内个数为1 mergeSort(arr, start, mid); mergeSort(arr, mid+1, end); // 将两个有序的序列进行组间合并 merge(arr, start, mid, end); } public static void main(String[] args){ int[] arr = new int[]{12, 3, 9, 24, 45, 17}; mergeSort(arr, 0, arr.length-1); for(int x : arr){ System.out.print(x + " "); } } }
基数排序:
对它的时间复杂度搞不懂,就只有代码了
public class RadixSort { public static int getNum(int[] arr){ int cnt = 0; for(int x : arr){ int t = 0; while(x != 0){ t++; x /= 10; } cnt = Math.max(cnt, t); } return cnt; } public static void iniCount(int[] count){ for(int j = 0; j < 10; j++){ count[j] = 0; } } public static void iniBucket(int[][] bucket){ for(int i = 0; i <10; i++){ for(int j = 0; j < 100; j++){ bucket[i][j] = 0; } } } public static void main(String[] args){ int[] arr = new int[]{2, 13, 497, 44, 56, 123, 65, 243, 120}; int[][] bucket = new int[10][100]; // 第二维的大小取值是看上面数组的大小而决定 int[] count = new int[10]; // 记录桶里的数字个数 // 首先找到 数组中 最大有几位数 int n = getNum(arr); for(int i = 1; i <= n; i++){ iniCount(count); iniBucket(bucket); for(int x : arr){ int t = x; int d = 0; for(int j = 0; j < i; j++){ // i=1时,取个位数字; i=2时,取十位数字 d = t % 10; t /= 10; } bucket[d][count[d]] = x; count[d]++; } // 把桶里的数字依次取出来 int k = 0; for(int x = 0; x < 10; x++){ for(int y = 0; y < count[x]; y++){ arr[k++] = bucket[x][y]; } } } for(int x : arr){ System.out.print(x + " "); } } }

