张正友标定法

0、张正友标定法论文

本篇博文参考张正友博士的两篇论文：Flexible camera calibration by viewing a plane from unknown orientation和 A Flexible New Technique for Camera Calibration

1、张正友标定法

首先，我们学习了相机成像模型，通过那个模型，很容易理解下面的公式。
在这里插入图片描述

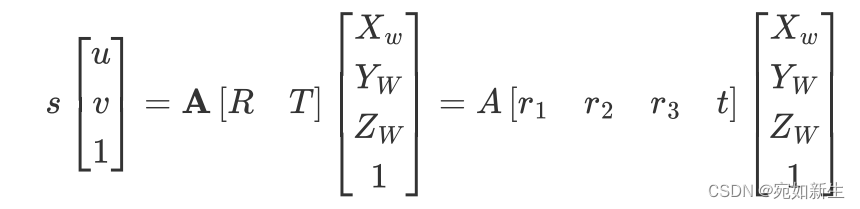
后面的 r i r_i ri​和 t t t是外参矩阵列向量表示形式，这样写的好处是可以利用旋转矩阵的性质来构建一些约束。

1.0 旋转矩阵的性质

    ①每一行每一列的模，都为1；
    ②任意两个列向量或者任意两个行向量都是正交的；
    ③正交矩阵的逆等于正交矩阵的转置。

后面会用到上面旋转矩阵的性质。

1.1 求解单应性矩阵

我们标定时使用的是平面标定板（这里以棋盘格为例），我们将 X O Y XOY XOY平面设置在标定板平面上， 轴垂直向外，这样对于检测的所有特征点都有
Zw​=0的关系。
在这里插入图片描述

带入上面那个式子，会有：

 

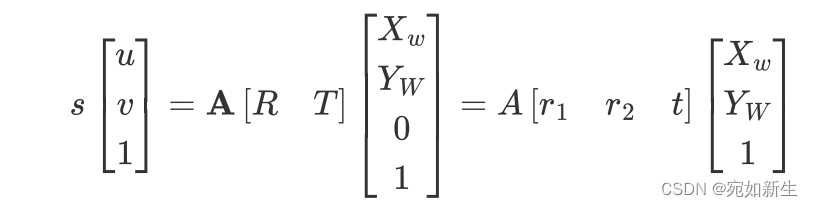
因为Zw​=0，所以我们消掉了r3​。
令$A [r 1 , r 2 , r 3] = H$，则有，
$s [ u , v , 1 ] ^T = H [ X_w , Y_w , 1 ] ^T $
这个*H*就是单应性矩阵，我们把它展开得到，

 

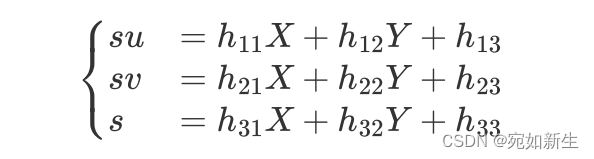
这样我们已知棋盘格上各个点的3D坐标（棋盘格的尺寸我们已知），以及图像平面上各个对应角点的像素坐标，就可以把$ h_{ij}$求解出来。

 

接着将 s带入前两个方程有，

也就是说， H有8个自由度。关于几种矩阵的自由度问题可以看这篇博客。
定义 $h' = [ h 11 , h 12 , h 13
h 21 , h 22 , h 23
h 31 , h 32 , 1 ]$,

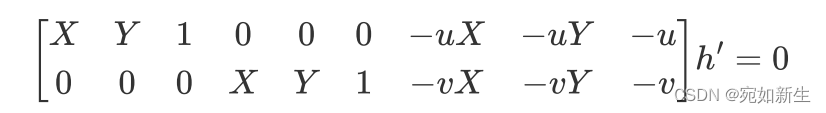
 以上$ X , Y , u , v $都是已知量。因为单应性矩阵有8个自由度，一对匹配点可以构建上面2个约束，所以4对匹配点就可以求解出单应性矩阵，由于噪声影响，现实中经常使用非线性优化的方法求解，比如奇异值分解+LM等。
我们将上式写为 $S h ′ = 0$ ,系数矩阵$S^TS$最小特征值对应的特征向量就是超定方程组$S h'= 0$的最小二乘解。

1.2 求解内参矩阵

我们上面求得的单应矩阵可能和真实的值存在一个尺度因子，我们增加一个尺度因子 , 有

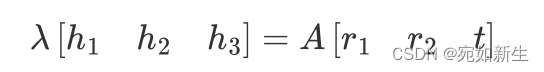
由1.0节提到的旋转矩阵的性质可得两个约束条件:

于是就有，

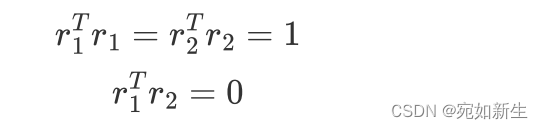
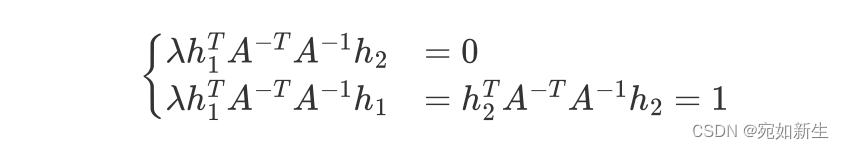
通过上面红字推导可知，图片中的公式其实是这样的$\lambda=\lambda^2$，我们认为它是一个常数尺度因子。就把他记为$ \lambda$即可。

因为A是内参矩阵，我们可以计算出他的逆矩阵。
$A=\left[\begin{array}{c} \alpha & \gamma &u_0 \\ 0 & \beta &v_0 \\ 0 & 0 &1 \\ \end{array}\right]$
$A^{-1}=\left[\begin{array}{c} \frac{1}{\alpha} & \frac{-\gamma}{\alpha \beta} &\frac{\gamma v_0-\beta u_0}{\alpha \beta} \\ 0 & \frac{1}{\beta} & -\frac{v_0}{\beta} \\ 0 & 0 &1 \\ \end{array}\right]$
其中， $\alpha,\beta$表示两方向上的焦距，$u_0,v_0$表示主点。早期的相机有可能会存在像素本身是平行四边形而非矩形的问题，因此增加一个参数&\gamma&来描述，这个参数同样可以认为是传感器的安置不严格与相机主光轴垂直造成的变形的近似，事实与像素坐标系的X，Y轴之间的夹角的正切值成反比，因此当 $\gamma=0$时，像素为矩形。
令$B=A^{-T}A^{-1}$，则有：

因为$ h_1$有三个元素嘛，所以有这种表示。
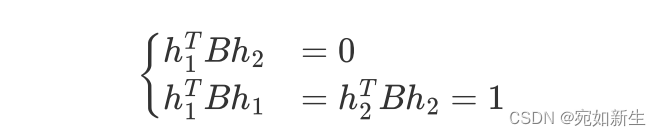
至于为什么我们把B矩阵铺成一个向量的时候，只留下了6个元素，其实算一算这个B就知道了。

 

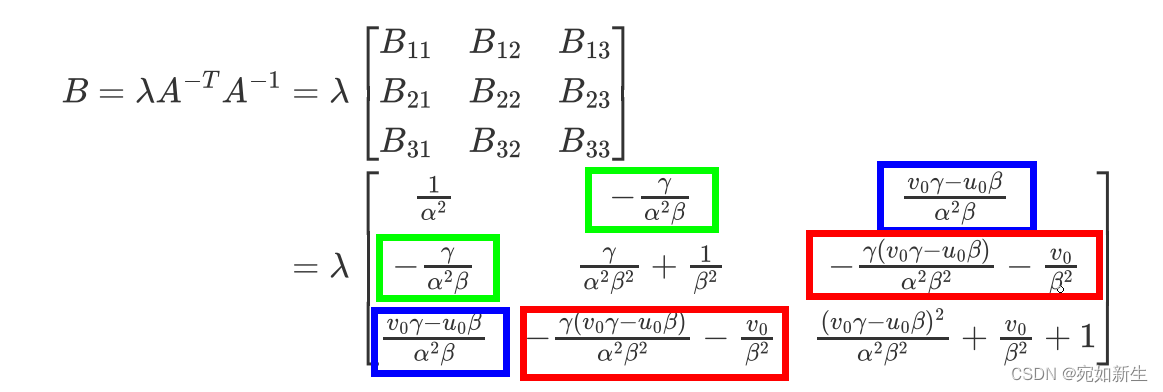
至此，之前的约束方程简化为：

 

其中，v中都是已知量，这又构成了一个Sh=0的方程。我们知道，每张标定图都可以提供一个上述约束关系(对应一个H)，而每个方程都会提供两个约束方程。 B本身有6个位置元素，因此理论上，三张标定图片就可以解出上述方程。当标定图超过3张时，也可以使用最小二乘法求解对应的超定方程。可以用奇异值分解和LM方法得到B.
得到B之后，就可以根据B与内参矩阵元素的关系解出$α , β , γ , u 0 , v 0 \alpha,\beta,\gamma,u_0,v_0 α,β,γ,u0​,v0$​来。

1.3 求解外参矩阵

我们知道（包含尺度因子在里面）
$[h_1,h_2,h_3] = A[r_1,r_2,t] [h1​,h2​,h3​]=A[r1​,r2​,t]$
这里面我们已经求解出了H和A，并且根据前面1.0节旋转矩阵的性质，所以有，

 

这时候就差一个$r_3$，很简单，
$ r_3=r_1Xr_2$（叉乘）。
到此为止，内外参都计算出来了。
由于图像存在噪声，所以我们得到的R其实并不一定满足正交的性质，因此使用优化的方法来得到最佳的R ,
在作者的原文中是这样说的：

 如果感兴趣可以自己去探索。

1.4 求解畸变系数

 

论文中：

 

1.5 非线性优化

注意：上面一系列操作都是为了得到各个参数的初值，有了初值，我们就可以利用相机模型+畸变模型对棋盘格上的3d点进行投影，建立重投影误差方程，然后利用非线性优化方法得到各个参数的准确值。
非线性优化方法介绍可以参考这篇文章。

2、单应性矩阵有什么用

关于单应性矩阵，我推荐阅读一下六哥的公众号文章神奇的单应性矩阵。
————————————————
版权声明：本文为CSDN博主「宛如新生」的原创文章，遵循CC 4.0 BY-SA版权协议，转载请附上原文出处链接及本声明。
原文链接：https://blog.csdn.net/Walking_roll/article/details/125821110