[数据结构]堆

建堆的两种方式

自上而下

这种方式的思路是，每插入一个节点，就向上比较，判断是否需要与其父节点进行交换，

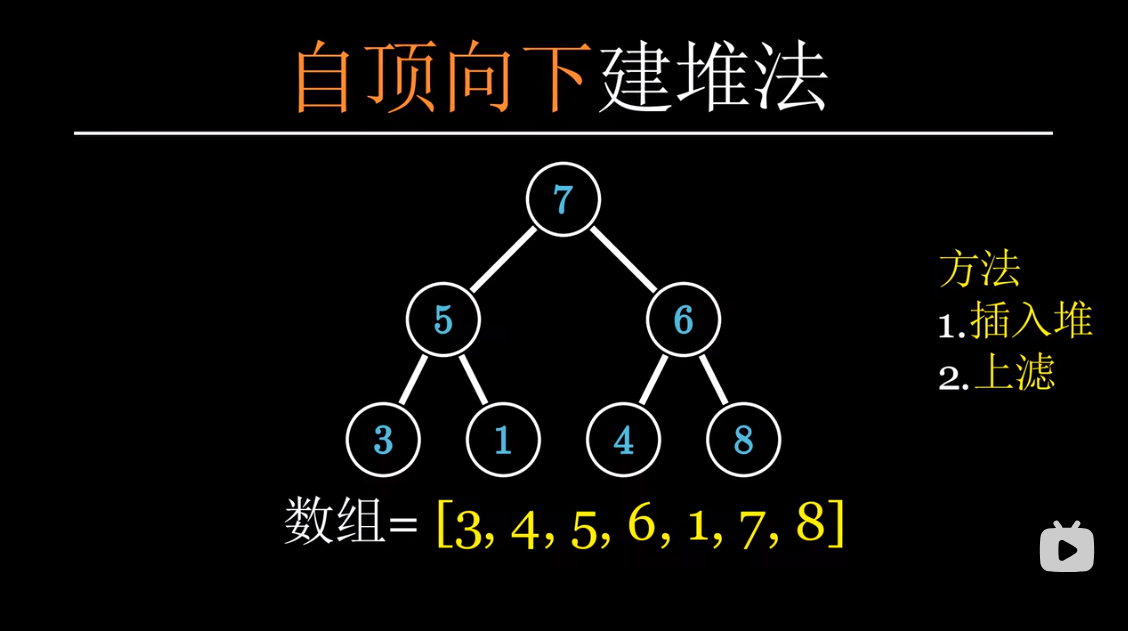
分析这种方式的时间复杂度，假设树的高度为h，以下均考虑最坏情况，也就是每一个节点都调整到根

第一层的1个节点不需要调整

第二层的2个节点，每个节点向上调整1次，2*1，

第三层的4个节点，每个节点向上调整2次，4*2，

第四层的8个节点，每个节点向上调整3次，8*3，

...

第h层的2^(h-1)个节点，每个节点向上调整h-1次，2^(h-1)*(h-1)

累计，

T(n) = 2^(1)*1+2^(2)*2+2^(3)*3+2^(4)*4+...+2^(h-1)*(h-1)

2*T(n) = 2^(2)*1+2^(3)*2+2^(4)*3+2^(5)*4+...+2^(h-1)*(h-2) +2^(h)*(h-1)

用T(n)-2*T(n)，

T(n)-2*T(n) = 2^1+2^2+2^3+...+2^(h-1)-2^(h)*(h-1)

​ = 2^h-2-2^h*(h-1)

把h=log2(n)代入

​ = 2^(log2(n))-2-2^(log2(n))*(log2(n)-1)

​ = n-2-n*(log2(n)-1)

保留最高项

T(n) = O(nlog2(n))

自下而上

先建立完全二叉树，然后从最后一个有叶子结点的节点开始向前调整。

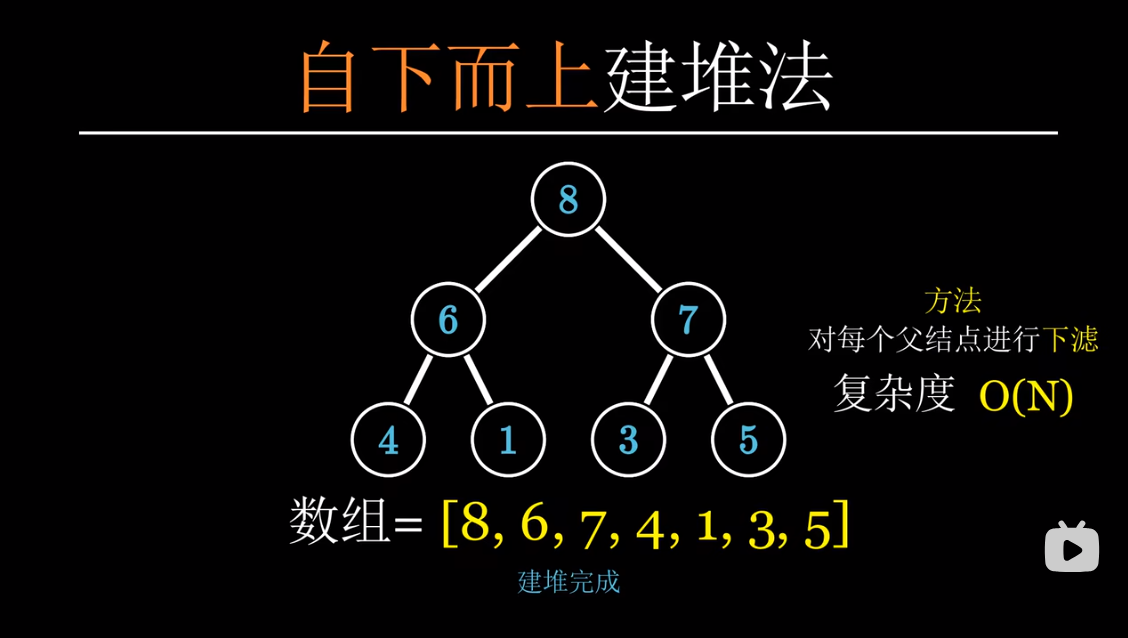
时间复杂度分析，假设树的高度为h，

第一层有1个节点，向下调整h-1次，1*(h-1)

第二层有2个节点，向下调整h-2次，2*(h-2)

第三层有4个节点，向下调整h-3次，4*(h-3)

第四层有8个节点，向下调整h-4次，8*(h-4)

...

第h-1层有2^(h-2)个节点，向下调整1次，

第h层有2^(h-1)个节点，向下调整0次，

T(n) = 2^0*(h-1)+2^1*(h-2)+2^2*(h-3)+2^3*(h-4)+...+2^(h-2)*1

2*T(n) = 2^1*(h-1)+2^2*(h-2)+2^3*(h-3)+2^4*(h-4)+...+2^(h-2)*2+2^(h-1)*1

---

2*T(n)-T(n) = -(h-1) + 2+2^2+2^3+2^4+...+2^(h-2)+2^(h-1)

​ = -(h-1)+2^h-2

带入h = log2(n)

T(n) = -(log2(n)-1)+n-2

保留最高项

T(n) = O(n)